
|
Читайте также: |
При решении задач о движении идеальной среды можно обратиться и непосредственно к уравнениям движения с соответствующими граничными условиями. В качестве примера рассмотрим движение бесконечного цилиндра в идеальной несжимаемой среде (рис. 7.26). Заметим, что такое движение можно рассматривать как плоское. Будем также полагать, что движение среды, вызываемое движением в
 Рис. 7.26
Рис. 7.26
| нем цилиндра, является потенциальным. Существенное отличие поставленной задачи от задачи обтекания неподвижного цилиндра плоскопараллельным поступательным потоком заключается в том, что рассматриваемое движение не является стационарным в неподвижной системе координат. Действительно, по мере продвижения цилиндра в неподвижной среде скорость индивидуальной частицы в каждой фиксированной точке |
пространства изменяется с течением времени. Вдали от цилиндра (на бесконечности0 будем полагать среду неподвижной. Несмотря на то, что задача является нестационарной, потенциал скорости должен удовлетворять уравнению Лапласа, не содержащему времени явно, т.е. 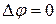 .
.
Так как на бесконечности 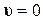 , но
, но 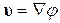 , то производные
, то производные 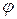 по координатам должны на бесконечности обращаться в нуль. Известно, что такими производными для цилиндрических задач являются производные
по координатам должны на бесконечности обращаться в нуль. Известно, что такими производными для цилиндрических задач являются производные 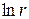 по координатам, начиная с первого порядка и выше, т.е.
по координатам, начиная с первого порядка и выше, т.е. 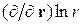 или
или  . Так как
. Так как 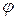 есть скалярная функция, а
есть скалярная функция, а 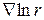 есть вектор, то общее выражение для искомого потенциала скорости
есть вектор, то общее выражение для искомого потенциала скорости 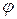 должно иметь вид:
должно иметь вид:
 (7.9.1)
(7.9.1)
Здесь вектор  есть некоторый независящий от координат вектор, который может быть связан только с единственным, имеющимся в нашем распоряжении вектором, от которого может зависеть решение - вектором скорости движения цилиндра
есть некоторый независящий от координат вектор, который может быть связан только с единственным, имеющимся в нашем распоряжении вектором, от которого может зависеть решение - вектором скорости движения цилиндра  . Эта связь может быть установлена из граничных условий на поверхности цилиндра:
. Эта связь может быть установлена из граничных условий на поверхности цилиндра:
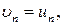
 (7.9.2)
(7.9.2)
Поскольку  , то из (7.9.1) следует
, то из (7.9.1) следует
 (7.9.3)
(7.9.3)
Используя (7.9.3), можно определить градиент потенциала скорости в виде
 (7.9.4)
(7.9.4)
После подстановки (7.9.3) в (7.9.2) можно получить
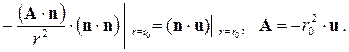 (7.9.5)
(7.9.5)
Таким образом, потенциал скорости j определяется соотношением
 (7.9.6)
(7.9.6)
Скорость движения индивидуальной частицы среды по определению равна
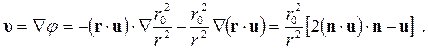 (7.9.7)
(7.9.7)
Из определения вектора скорости  согласно (7.9.7) и рис.7.26 легко найти компоненты скорости
согласно (7.9.7) и рис.7.26 легко найти компоненты скорости  и
и  :
:
 (7.9.8)
(7.9.8)
Данные значения компонент скоростей определены в системе координат, двигающейся со скоростью  . В этой системе координат ни
. В этой системе координат ни 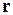 , ни
, ни  и
и  не зависят от времени t.
не зависят от времени t.
Таким образом, в каждый момент времени распределение скоростей вокруг двигающегося цилиндра удовлетворяет уравнениям (7.9.8). Поэтому с точки зрения наблюдателя, двигающегося вместе с цилиндром, картина движения среды около цилиндра стационарна.
Следует заметить, что из полученного решения можно получить обтекание неподвижного цилиндра, если на движение, описываемое формулами (7.6.32), наложить движение всей среды вместе с цилиндром с постоянной скоростью  , направленной справа налево. Тогда будет иметь место обтекание неподвижного цилиндра плоскопараллельным поступательным потоком с направленной справа налево скоростью
, направленной справа налево. Тогда будет иметь место обтекание неподвижного цилиндра плоскопараллельным поступательным потоком с направленной справа налево скоростью  . Распределение скоростей такого движения описывается полученными выше формулами (7.6.9), если в них изменить знак скорости набегающего потока и заменить скорость
. Распределение скоростей такого движения описывается полученными выше формулами (7.6.9), если в них изменить знак скорости набегающего потока и заменить скорость  скоростью u:
скоростью u:
 (7.9.8а)
(7.9.8а)
Дата добавления: 2015-08-03; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка задачи и сущность метода | | | Распределение давления около движущегося цилиндра |