Обтекание бесконечного цилиндра с циркуляцией

При потенциальном движении идеальной, несжимаемой среды потенциал скорости 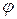должен удовлетворять уравнению Лапласа (7.5.7)

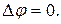
Уравнение Лапласа является линейным уравнением относительно потенциала скорости 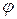. Следовательно, сумма любых его решений также является его решением. Поэтому, суммируя известные простейшие решения уравнения Лапласа, можно получить решения, имеющие во многих случаях вполне реальный смысл и практическое значение. Очевидно:

(7.7.1)

Таким образом, скорость сложного движения определяется суммой векторов скоростей простых движений.

Наложим на потенциальное движение среды со скоростью при обтекании цилиндра плоский вихрь с интенсивностью (или циркуляцией) 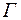, вращающийся против часовой стрелки

(7.7.2)

Суммируя согласно (7.7.1) скорости простых движений, получим скорость сложного движения с компонентами, которые с учетом (7.6.9), (7.7.1) и (7.7.2) равны:

(7.7.3)

Для построения линий тока найдем положение критических точек на поверхности цилиндра при 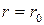. В критических точках А и В на поверхности цилиндра (см. рис. 7.18). Следовательно, должны обращаться в нуль как , так и 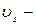компоненты скорости . Радиальная компонента скорости на поверхности цилиндра в любой точке равна нулю. Касательная же компонента скорости 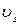равна нулю в точках, определяемых соотношением (7.7.3) для 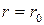, т.е.

(7.7.4)

Возможны следующие случаи:

1. Если (обтекание цилиндра без циркуляции), то имеет место прежний результат (см. п. 7.6.4) и

2. Если 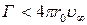, то критические точки А и В находятся на верхней половине поверхности цилиндра, т.к. лежит в пределах

3. Если 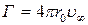, то обе точки сливаются в одну при .

4. При не существует при , и критических точек на поверхности цилиндра не существует; они могут быть расположены только в поле течения среды..

Картина линий тока для этих случаев представлена на рис. 7.20а, б, в, г.

Дата добавления: 2015-08-03