Вихревая трубка. Теорема Гельмгольца

Аналогично линии тока можно ввести понятие вихревой линии. Вихревая линия - это линия, касательная к которой в данной точке определяет направление ротора скорости в этой точке. Очевидно, уравнение вихревой линии имеет вид:

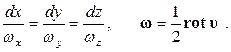(7.4.6)

Здесь 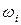- i -я компонента (i = x, y, z) угловой скорости мгновенного поворота.

Аналогично трубке тока можно построить вихревую трубку. Рассмотрим некоторый контур, охватывающий малую площадку DS. Через каждую точку этого контура проведем вихревую линию. Тогда совокупность этих линий ограничит вихревую трубку. Скалярное произведение 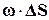называют интенсивностью вихревой трубки.

Теорема Гельмгольца утверждает, что интенсивность вихревой трубки неизменна по её длине и не зависит от времени.

Рассмотрим некоторую вихревую трубку (рис.7.6). Вычислим поток вектора 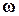через поверхность S, ограничивающую некоторый объём V трубки. Используя теорему Гаусса-Остроградского, можно записать

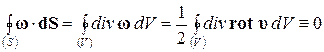, (7.4.7)

т.к. из векторной алгебры известно, что div rot º 0. Разделим интеграл по поверхности на две части: интеграл по боковой поверхности и интеграл по торцевым площадкам 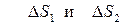. Очевидно, что по определению вихревой трубки интеграл по боковой поверхности равен нулю. Интеграл по элементарным

Рис.7.6

торцевым площадкам можно записать в виде суммы двух слагаемых: Принимая во внимание направление единичных нормальных векторов к этим площадкам, получим Можно было бы вдоль трубки тока построить не две, а несколько площадок и, следовательно, можно затем записать:

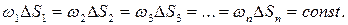(7.4.8)

Из последнего соотношения следует, что интенсивность вихревой трубки постоянна вдоль трубки, т.е. не зависит от радиуса вектора 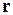. В силу же теоремы Томсона можно записать

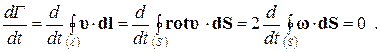(7.4.9)

Следовательно, для интенсивности вихревой трубки имеем:

(7.4.10)

т.е. интенсивность вихревой трубки не зависит от времени.

Таким образом, интенсивность вихревой трубки сохраняется в пространстве и с течением времени. Если в начальный момент времени интенсивность вихревой трубки была равна нулю , то она будет равна нулю и во все последующие моменты времени. Если же в начальный момент времени интенсивность вихревой трубки не равна нулю 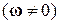, то она сохраняется и во все последующие моменты времени. То есть, вихревое движение в идеальной жидкости не возникает и не уничтожается, что и составляет содержание теоремы Гельмгольца.

Рис.7.7

Следовательно, вихревые трубки не могут начинаться и заканчиваться внутри жидкости. Они должны быть или замкнутыми, или начинаться и заканчиваться на поверхности твёрдых тел или на свободной поверхности жидкости.

Так как теорема Томсона справедлива лишь для баротропных движений в поле потенциальных сил, то источником возникновения вихревых движений могут, очевидно, быть или не потенциальные силы вязкости, или не баротропность движения.

Дата добавления: 2015-08-03