Читайте также:
|
Уравнение сохранения энтропии (7.1.4) свидетельствует о том, что, если в начальный момент времени во всех точках объёма, занятого идеальной средой, энтропия была одинакова, то она останется той же самой во всех точках и во все последующие моменты времени. Тогда из уравнения (7.1.4) можно записать:
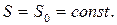
Движение жидкости с постоянным значением энтропии называют изоэнтропическим.
Используя условие изоэнтропичности движения (7.1.4), уравнению движения идеальной жидкости (7.1.2) можно придать другой вид. Для этого воспользуемся определением малого изменения энтальпии единицы массы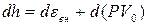 
и основным термодинамическим равенством (4.2.1) для замены малого изменения внутренней энергии в виде:
где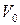 
- удельный объём жидкости.
Так как для изоэнтропического движения dS = 0, то имеем:
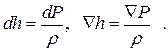(7.1.11)
Эти соотношения означают, что при движении идеальной среды индивидуальная частица испытывает сжатие при увеличении давления. Тогда уравнение движения в системе уравнений сохранения (7.1.5) принимает вид:
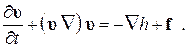(7.1.12)
Дата добавления: 2015-08-03; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Движение несжимаемой среды | | | Граничные и начальные условия |