Движение несжимаемой среды

Условием несжимаемости среды, как отмечалось ранее, является уравнение 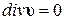. В этом случае из уравнения непрерывности (6.3.3) следует, что dρ/dt =0, т.е. массовая плотность не зависит ни от координат физического пространства х_i, ни от времени t. Тогда в уравнении Эйлера (7.1.2) плотность ρ можно внести под знак производной и уравнение записать в векторном виде

(7.1.6)

Для изоэнтропических движений несжимаемой среды уравнение (7.1.6) можно преобразовать к виду, содержащему только скорость. Для этого предположим, что внешние силы являются потенциальными, т.е. . Воспользуемся известной формулой из векторного анализа вида

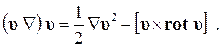(7.1.7)

После подстановки (7.1.7) в уравнение движения (7.1.6) получим:

(7.1.8)

Применив операцию rot к обеим частям уравнения (7.1.8) и учитывая, что rot Ѻ0, имеем:

(7.1.9)

Данное уравнение называют уравнением Эйлера в форме Громека. Это уравнение замечательно тем, что оно содержит только вектор скорости. Таким образом, в случае течений несжимаемых сред, если массовые силы являются потенциальными, скорости могут быть найдены независимо от других параметров течения.

При заданных краевых и начальных условиях решение уравнения (7.1.9) существует и оно единственное, т.е. задача становится чисто кинематической. Для отыскания других переменных характеристик течения необходимо, зная , вернуться к исходной форме уравнения движения Эйлера (7.1.6). Например, плотность может быть найдена из уравнения непрерывности, а — из уравнения движения Эйлера (7.1.6).

Если ввести аксиальный вектор w соотношением , то уравнение Громека можно записать в виде

. (7.1.10)

Дата добавления: 2015-08-03