Замкнутая система уравнений сохранения для идеальной среды

Идеальная среда

Под жидкостью будем понимать как собственно саму жидкость, так и газ, полагая, что оба эти агрегатных состояния вещества представляют собой сплошную среду.

Идеальной жидкостью называют жидкость, у которой отсутствует вязкое трение и объёмная вязкость (h = 0, z = 0), теплопроводность (l = 0), а модуль сдвига равен 0 (m = 0). Несмотря на то, что это весьма идеализированная модель сплошной среды, многие характерные черты движения жидкостей могут быть изучены при помощи этой простейшей модели, по крайней мере, вдали от поверхности обтекаемых тел.

Уравнения движения для сжимаемой и несжимаемой идеальной среды

Замкнутая система уравнений сохранения для идеальной среды

В пренебрежении вязкостью для идеальной ньютоновской среды общий тензор напряжений согласно (6.11.2) имеет простой вид:

. (7.1.1)

Поэтому уравнение движения идеальной среды в соответствии с уравнением (6.4.9) можно записать в следующей форме:

(7.1.2)

Вообще говоря, можно было бы ослабить условие идеальности и полагать, что вязкость жидкости настолько мала, что . Однако это условие заведомо не выполняется вблизи поверхности обтекаемых тел.

Уравнение (7.1.2) называют уравнением Эйлера. Уравнение непрерывности движения (6.3.5), конечно, сохранит свой вид. Уравнение сохранения внутренней энергии согласно уравнению (6.7.7) и уравнению (6.7.1) можно записать в виде

, (7.1.3)

поскольку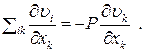

Из второго уравнения системы – уравнения сохранения энтропии (6.7.10) следует физически очевидный результат:

, (7.1.4)

т.е. энтропия единицы массы индивидуальной частицы идеальной жидкости сохраняется в процессе движения. Этот результат очевиден, т.к. сделанные выше предположения лишили жидкость механизмов возрастания энтропии.

Таким образом, система уравнений сохранения для идеальной жидкости имеет вид:

(7.1.5)

Таким образом, имеется пять уравнений для нахождения семи неизвестных искомых функций (если внешние силы заданы): Для замыкания системы уравнений (7.1.5.) до полной необходимо добавить термическое уравнение состояния:

Внутренняя энергия e_вн также может быть определена из калорического уравнения состояния:

Дата добавления: 2015-08-03