Читайте также:
|
Движение жидкости, при котором во всем занятом движущейся жидкостью пространстве 
, называют потенциальным.
Рассмотрим в качестве массовой силы силу тяжести. Тогда, если ось z направлена в противоположную ускорению силы тяжести сторону, можно записать:
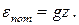
Тогда для стационарного (
) и потенциального (
) движения идеальной несжимаемой среды в поле тяжести из уравнения (7.1.8) следует
(7.2.1)
В любой точке потока последнее равенство может выполняться только тогда, когда выражение в скобках равно некоторой постоянной во всем поле течения среды, не зависящей от координат, т.е.
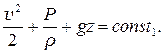
(7.2.2)
Уравнение (7.2.2) есть первый интеграл уравнения движения Эйлера (7.1.2), и его называют уравнением Бернулли для несжимаемой идеальной жидкости. Уравнение Бернулли по физическому смыслу является уравнением сохранения полной энергии единицы массы. Действительно, в нём слагаемые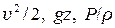 
есть кинетическая энергия, потенциальная энергия и работа сил давления по изменению объема единицы массы, соответственно.
Для сжимаемой среды при изоэнтропическом движении массовая плотность не зависит от радиуса-вектора r и 
Поэтому в соответствии с (7.1.11) можно записать
.
Используя эту замену в (7.2.2), получаем уравнение Бернулли для несжимаемой жидкости при изоэнтропическом движении в форме
(7.2.3)
Дата добавления: 2015-08-03; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Граничные и начальные условия | | | Линии тока и траектории. Трубка тока |