Влияние сжимаемости среды

Как видно из соотношения (7.2.15), давление в критической точке больше, чем давление жидкости вдали от тела, на величину скоростного напора . Таким образом, индивидуальная частица газа или жидкости при движении по критической линии тока испытывает сжатие. При этом её плотность увеличивается. Это явление изменения плотности будет наблюдаться и для частиц, движущихся по другим линиям тока. Однако наиболее значительное изменение, очевидно, будет наблюдаться для частиц на критической линии тока. Поэтому, если учесть сжимаемость среды, то давление в критической точке должно иметь некоторое другое значение, учитывающее, что плотность среды вдали от тела и в критической точке не равны, как это предполагалось при выводе формулы (7.2.15).

Оценим влияние сжимаемости среды на давление в критической точке. Если среда несжимаема, то давление в критической точке определяется согласно (7.2.15). Для сжимаемой среды необходимо воспользоваться уравнением Бернулли в форме (7.2.2) в отсутствии поля тяжести и, учитывая изменение энтальпии единицы массы, запишем его для критической линии тока в виде

(7.3.1)

Будем полагать, что сжатие индивидуальных частиц, движущихся по критической линии тока с достаточно большой скоростью, происходит адиабатически, т.е. без теплообмена с другими частицами. В этом случае, как было показано в п.7.1.1, имеем

Так как адиабатическое сжатие индивидуальной частицы на критической линии тока описывается уравнением Пуассона (или уравнением адиабаты), то очевидны следующие преобразования при вычислении энтальпии h единицы массы:

(7.3.2)

Здесь 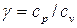- показатель адиабаты. Интегрируя с точностью до несущественной произвольной постоянной интегрирования, получим:

(7.3.3)

Подставляя значение (7.3.3) в уравнение Бернулли (7.3.1), имеем

(7.3.4)

Отношение плотностей возможно найти из уравнения Пуассона, подстановка которого в (7.3.4) позволяет определить :

(7.3.5)

Полагая, что второе слагаемое мало по сравнению с единицей, представим (7.3.5) как бином Ньютона:

.

Следовательно, давление сжимаемой среды в точке полного торможения равно:

(7.3.6)

Сравнивая полученное выражение с формулой (7.2.13), можно сделать следующее заключение: если справедливо соотношение

(7.3.7)

то формула (7.3.6) переходит в формулу (7.2.15) для несжимаемой среды. Таким образом, при выполнении неравенства (7.3.7) необходимо среду (жидкость, газ) рассматривать несжимаемой.

Как показано в п.6.12, скорость адиабатического распространения продольных волн сжатия в ньютоновских средах равна . Но согласно (5.2.7) адиабатический модуль , поэтому имеем:

(7.3.8)

Для идеальной среды в адиабатическом процессе производную можно найти из уравнения адиабаты , после подстановки которой в (7.3.8) получим:

(7.3.9)

Скорость называют скоростью звука, т.е. скорость звука является скоростью распространения продольных волн сжатия в среде. Тогда неравенство (7.3.7) можно записать в следующем виде

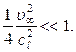(7.3.10)

Таким образом, если скорость движения среды значительно меньше скорости звука в ней, то ее можно рассматривать как среду несжимаемую. Например, если воздух (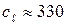 м/сек) движется со скоростью = 70 м/сек, то максимальная поправка к давлению в критической точке составит %, что можно не учитывать в большинстве инженерных расчётов и теоретических рассмотрений.

Дата добавления: 2015-08-03