Линии тока и траектории. Трубка тока

Линия тока - это линия, касательная к которой в точке касания даёт направление скорости индивидуальной частицы. Траектория - это линия или кривая, описываемая индивидуальной частицей при своём движении. При установившемся движении линии тока и траектории совпадают. При неустановившемся движении это, вообще говоря, разные линии.

Для визуализации течения в экспериментах вводят в движущуюся жидкость мелкие, легкие частицы, которые при соответствующем освещении довольно ярко светятся. Если сфотографировать поле течения с небольшой выдержкой, то на фотографии можно наблюдать множество коротких черточек, «прочерчиваемых» за короткое время экспозиции на фотопластинке множеством светящихся частиц порошка. Можно подобрать к некоторому последовательному ряду чёрточек кривые, к которым эти чёрточки являются касательными, эти кривые и будут линиями тока в жидкости в данный момент времени. В другой момент времени неустановившегося движения линии тока могут быть другими. Если же значительно увеличить время экспозиции, то каждая частица «прочертит» на фотопластинке непрерывную линию через всё поле течения, охватываемое объективом. Эти линии и являются траекториями частиц жидкости.

Касательные к линии тока в различных её точках дают направление скорости различных индивидуальных частиц в данный момент времени. Касательные к траектории в различных её точках дают направление скорости одной и той же индивидуальной частицы в различные моменты времени.

Если в жидкости взять некоторый замкнутый контур и через все его точки провести линии тока, то они составят некоторую трубку, которую называют трубкой тока. Трубка тока замечательна тем, что по определению через её боковую поверхность нет потока жидкости. Жидкость в трубку тока может поступать только через её торцы. Элемент длины линии тока dr и скорость частицы u являются векторами коллинеарными, для которых отношение соответствующих компонент есть величина постоянная. Поэтому уравнение линии тока имеет вид

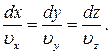(7.2.4)

Рассмотрим стационарное (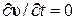), не потенциальное (), изоэнтропическое () движение сжимаемой жидкости в поле потенциальных сил (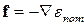). Спроектируем уравнение (7.1.9) на линию тока. Для этого умножим скалярно правую и левую часть уравнения (7.1.9) на единичный вектор l, касательный к линии тока:

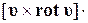l = 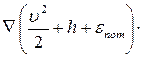l. Но векторное произведение в левой части данного уравнения представляет собой вектор, перпендикулярный вектору , а, следовательно, и l. Поэтому их скалярное произведение равно нулю. Тогда имеем:

l (7.2.5)

Здесь означает производную вдоль направления единичного вектора l. Следовательно, для данной линии тока справедливо уравнение Бернулли вида

(7.2.6)

Это уравнение является уравнением Бернулли для линии тока при стационарном, потенциальном движении идеальной сжимаемой жидкости в поле потенциальных сил тяжести. Уравнение (7.2.6) отличается от уравнения (7.2.2) только тем, что в случае не потенциального () движения жидкости в потенциальном поле силы тяжести константа в правой части уравнения (7.2.2) постоянна во всём поле течения жидкости. Тогда как в уравнении (7.2.6) константа в правой части является постоянной лишь для данной линии тока при не потенциальном движении, когда , в поле потенциальных сил тяжести и может иметь другое значение для другой линии тока. Для несжимаемой же жидкости при не потенциальном движении для линии тока уравнение Бернулли имеет вид:

(7.2.7)

Следует заметить, что возможно получить уравнение Бернулли в виде (7.2.7) каждый раз, когда удаётся выразить слагаемое (1/ r) в виде градиента некоторой функции. Так, для изоэнтропического движения сжимаемой идеальной жидкости 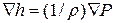, а для несжимаемой идеальной жидкости Очевидно, что это можно сделать и при изотермическом движении, когда Тогда выражение можно выразить в виде градиента некоторой функции Ф(Р) в виде

Такие движения называются баротропными, а функцию Ф (P) называют баротропным потенциалом. Для баротропных движений уравнение Бернулли имеет вид

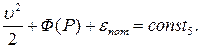(7.2.8)

Дата добавления: 2015-08-03