Обтекание плоской пластинки идеальной несжимаемой жидкостью

Рассмотрим потенциальное ()обтекание неограниченно широкой плоской пластины однородным потоком идеальной несжимаемой жидкости. Очевидно, что картина обтекания будет идентична во всех плоскостях, перпендикулярных пластинке. Поэтому достаточно рассмотреть движение жидкости в одной из плоскостей.

Рис.7.15

Пусть пластинка длиной 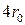(рис.7.15) расположена вдоль оси комплексной плоскости . Пусть далее скорость набегающего потока на пластинку вдали от нее постоянна, равна и направлена вдоль оси . Картина обтекания в данном случае очевидна. Действительно, т.к. идеальная жидкость может беспрепятственно скользить вдоль пластинки, то пластинка вообще не оказывает никакого

воздействия на поток, т.е. потенциальный плоскопараллельный набегающий поток останется таковым вблизи пластинки и после неё. Тогда линии тока (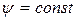) такого обтекания будут линиями, параллельными оси , а линии равного потенциала (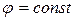) - перпендикулярными к ней. Принимая во внимание вышесказанное, имеем:

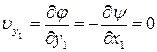, . (7.6.3)

Из первого равенства (7.6.3) имеем:

, . (7.6.4)

Из второго равенства (7.6.3) следует очевидный факт, что потенциал скорости , которая не зависит от , а функция тока , которая не зависит от . Поэтому эти функции не зависят ни от , ни от и несущественны, т.к. определяются лишь началом отсчёта и можно их положить равными нулю.

Составим комплексный потенциал :

, (7.6.5)

Здесь - комплексная переменная в плоскости .

Далее используем конформное отображение точек комплексной плоскости 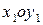в точки комплексной плоскости с переменной в виде

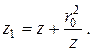(7.6.6)

Из (7.6.6) следует

Рассмотрим, как точки области плоскости преобразуется в точки плоскости . Пластинка в плоскости x ₁ oy ₁ описывается уравнениями 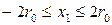. Тогда предыдущее равенство принимает вид:

Таким образом, уравнение пластинки в плоскости xoy имеет вид:

. (7.6.7)

Это уравнение есть уравнение окружности радиуса . Причем, точки плоскости , имеющие 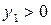или , как нетрудно показать, попадают вне круга.

Таким образом, если в комплексной плоскости имеет место обтекание пластинки шириной 4 r ₀ однородным плоскопараллельным потоком среды, то в плоскости z при помощи конформного отображения (7.6.6) оно преобразуется в поперечное обтекание этим же потоком бесконечного цилиндра радиусом r ₀ Причем, общие свойства конформных отображений гарантируют, что в точках, удалённых на бесконечность, сохраняется направление линий j = const и y = const и их ортогональность в любой точке пересечения.

Дата добавления: 2015-08-03