Метод конформных отображений

В соответствии с определениями потенциала скорости j (7.5.1) и функции тока y (7.5.6) для плоского, потенциального движения идеальной несжимаемой жидкости компоненты и скорости индивидуальной частицы равны:

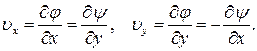(7.6.1)

Но соотношения (7.6.1) для функций j и y представляют собой известные условия Коши - Римана для комплексной функции вида

w = j + iy, w = w (z),

где комплексная функция w является аналитической функцией комплексного аргумента z = x + iy, т.е. функция w (z) в каждой точке комплексной плоскости имеет определенную производную

(7.6.2)

Функцию w (z) называют комплексным потенциалом, а производную - комплексной скоростью.

Таким образом, используя теорию функций комплексного переменного, имеется возможность иметь дело не с двумя функциями j и y от двух аргументов x и y, а лишь с одной комплексной функцией w от одного комплексного переменного z.

Кроме того, начиная с решения какой-либо тривиальной задачи, методами конформных отображений можно получить решение целого ряда более сложных задач, прямое решение которых часто бывает затруднительно.

Дата добавления: 2015-08-03