Читайте также:
|
Движение среды называют плоским, если все характеристики движения зависят только от двух координат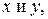 
или плоское движение - это такое движение, при котором во всех плоскостях, параллельных координатной плоскости 
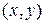, его характеристики одинаковы.
Для описания плоского потенциального движения несжимаемой среды удобно ввести ещё одну функцию - функцию тока. Эту скалярную функцию 
определяют следующим образом:
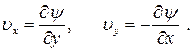(7.5.6)
Можно показать, что функция тока условию несжимаемости удовлетворяет автоматически по ее определению (7.5.6). Действительно, имеем
, 
.
Для плоского потенциального движения имеем:
, 
, 
, 
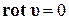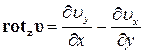(7.5.7)
Таким образом, при плоском потенциальном движении несжимаемой среды, как потенциал скорости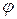 
, так и функция тока должны удовлетворять уравнению Лапласа, т.е. они являются гармоническими функциями. При непотенциальном движении функция тока должна удовлетворять уравнению, которое можно получить, подставляя (7.5.6) в уравнение Громека (7.1.10). Очевидно, что функция тока может быть введена только для плоского движения среды.
Дата добавления: 2015-08-03; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Потенциал скорости. Граничные условия | | | Свойства функции тока |