
|
Читайте также: |
Функция тока обладает рядом свойств, которые оправдывают её введение:
1. Линии тока - это линии, которые удовлетворяют уравнению 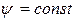 .
.
Действительно, уравнение линии тока имеет вид:
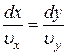 ,
, 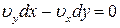 ,
, 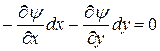 ,
, 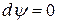 ,
, 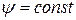 .
.
2. Если на плоскости 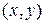 между двумя точками, лежащими на двух различных линиях тока, провести некоторую произвольную кривую, то поток среды через эту кривую будет определяться разностью значений функций тока для этих линий тока.
между двумя точками, лежащими на двух различных линиях тока, провести некоторую произвольную кривую, то поток среды через эту кривую будет определяться разностью значений функций тока для этих линий тока.
Действительно, расход жидкости Q через линию 1-2, а точнее через площадку единичной ширины в направлении оси z со стороной dl в плоскости (x,y) (рис.7.14), равен:
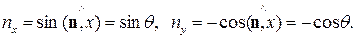
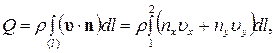


Далее, из рис 7.14 очевидны соотношения: 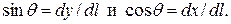 Подставляя полученные соотношения в формулу для расхода Q и используя определение функции тока (7.5.6), получим:
Подставляя полученные соотношения в формулу для расхода Q и используя определение функции тока (7.5.6), получим:
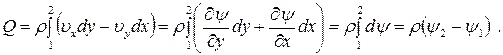 (7.5.8)
(7.5.8)
3. Линии тока 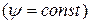 и линии равного потенциала
и линии равного потенциала 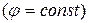 взаимно ортогональны в каждой точке поля течения.
взаимно ортогональны в каждой точке поля течения.
Направления нормальных единичных векторов к этим линиям определяются соотношениями:
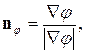
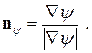
Скалярное произведение этих единичных векторов равно:
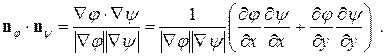
 Рис.7.14 Рис.7.14
| Но согласно определения потенциала скорости j (7.5.1) и функции тока y (7.5.6) легко видеть, что и последнее соотношение равно нулю. Действительно:
 (7.5.9)
Таким образом, линии семейства (7.5.9)
Таким образом, линии семейства 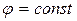 и линии семейства и линии семейства 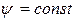 в точках пересечения взаимно ортогональны, т.е. пересекаются под прямым углом под прямым углом. в точках пересечения взаимно ортогональны, т.е. пересекаются под прямым углом под прямым углом.
|
Дата добавления: 2015-08-03; просмотров: 141 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Функция тока для плоского движения идеальной среды | | | Метод конформных отображений |