Потенциал скорости. Граничные условия

Движение идеальной среды называют потенциальным, если в любой точке пространства, занятого движущейся средой, 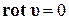. Поэтому скорость может быть представлена в виде градиента некоторой скалярной функции 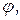называемой потенциалом скорости, т.е.

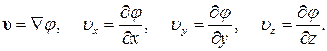(7.5.1)

Действительно, если скорость может быть представлена в виде градиента скалярной функции, то движение потенциально, т.к.

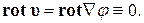
Для потенциального движения 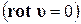циркуляция по любому замкнутому индивидуальному или неиндивидуальному контуру в односвязной области течения равна нулю, т.е.

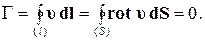
Это означает, что при потенциальном движении не может быть замкнутых линий тока, т.к. в противном случае (линия тока совпадает с замкнутым контуром интегрирования) циркуляция скорости была бы отлична от нуля.

Баротропное нестационарное движение в поле сил тяжести описывается уравнением Эйлера (7.1.9, 7.2.8)

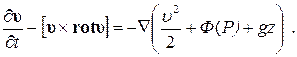(7.5.2)

Но для потенциального движения идеальной среды согласно (7.5.1) имеем

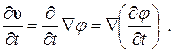
Поэтому из (7.5.2) следует уравнение вида

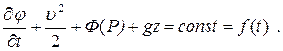(7.5.3)

Постоянная в правой части уравнения (7.5.3) при нестационарном движении может зависеть от времени, однако в данный момент времени она одинакова для всех точек пространства, занятого средой. Поскольку конечной целью является нахождение скорости движения среды, а скорости определяются производными от потенциала 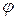по координатам согласно (7.5.1), то любая функция времени, добавленная к потенциалу, не изменит результата при вычислении скоростей. Заменяя 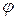на 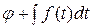в левой части (7.5.3), получаем в правой части уравнения (7.5.3) нуль. Поэтому без ограничения общности рассмотрения можно в уравнении (7.5.3) функцию 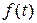положить равной нулю.

Для стационарного движения 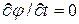и из уравнения (7.5.3) следует обычное уравнение Бернулли с постоянной в правой части, не зависящей ни от координат, ни от времени.

Ранее было показано, что для идеальной среды, которая является несжимаемой, должно выполняться условие div u = 0. Но согласно (7.5.1) это условие дает уравнение

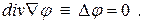(7.5.4)

Таким образом, при стационарном потенциальном движении несжимаемой среды необходимо найти лишь одну скалярную функцию 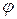, которая удовлетворяет уравнению Лапласа (7.5.4). Поскольку при нестационарном движении потенциал скорости 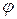должен быть функцией не только координат, но и времени, согласно (7.5.3), а уравнение Лапласа содержит лишь производные по координатам, то отсюда следует, что время в 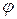может быть введено только через граничные условия.

Граничные условия для идеальной среды в каждой точке поверхности обтекаемого тела имеют вид

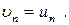
Здесь 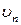- нормальная к поверхности обтекаемого тела компонента скорости среды, 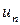- нормальная компонента скорости движения элемента поверхности тела (если поверхность неподвижна, то 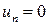). Для потенциального движения граничные условия можно записать в виде:

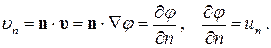(7.5.5)

Величина 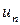должна быть задана как функция координат и времени, т.е.

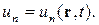
Таким образом, потенциал 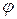в любой точке несжимаемой среды зависит от времени так же, как и потенциал на поверхности обтекаемого тела. Так, если при движении тела в идеальной несжимаемой среде создаваемое им движение является потенциальным, то в каждый момент времени потенциал во всех точках среды зависит лишь от скорости движения тела в тот же момент времени.

Физически это можно понять, если принять во внимание, что возмущение, а следовательно, и взаимодействие между различными частями несжимаемой среды распространяется с бесконечной скоростью. Поэтому изменение скорости в какой-либо точке на поверхности ведёт к мгновенному изменению скоростей во всех точках поля течения идеальной несжимаемой среды.

Дата добавления: 2015-08-03