
|
Читайте также: |
Рассмотрим картину обтекания цилиндра в плоскости xoy (рис.7.16). Най-дём комплексный потенциал w в точке с радиус-вектором r в полярной системе координат ( ):
):
 .
.
Умножая числитель и знаменатель дроби выражения в скобках на комплексно сопряженное число, получаем:

Из этого определения w следуют следующие формулы для 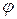 и
и  :
:
 ,
, 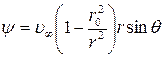 . (7.6.8)
. (7.6.8)
Из любого определения (7.6.8) для 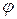 или
или  можно теперь вычислить компоненты
можно теперь вычислить компоненты  и
и 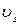 скорости
скорости  в точке
в точке 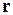 :
:
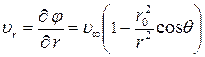 ,
,  (7.6.9)
(7.6.9)
 Рис.7.16
Рис.7.16
| Пользуясь полученными выражениями (7.6.8), нетрудно построить линии тока ( ) и линии равного потенциала - потенциальные линии ( ) и линии равного потенциала - потенциальные линии ( ). Если ввести безразмерный модуль радиус-вектора ). Если ввести безразмерный модуль радиус-вектора 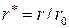 и безразмерный расход и безразмерный расход 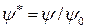 , где , где  есть расход жидкости вдали от обтекаемого цилиндра через площадку высотой есть расход жидкости вдали от обтекаемого цилиндра через площадку высотой  и единичной длины, то второе уравнение (7.6.8) приводится к виду и единичной длины, то второе уравнение (7.6.8) приводится к виду
|
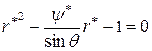 .
.
Задавая величины  , где m и n имеют целочисленные значения, и углы
, где m и n имеют целочисленные значения, и углы  , возможно по известной квадратурной формуле вычислить значения
, возможно по известной квадратурной формуле вычислить значения 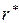 и r, а затем построить линии тока. Аналогично строятся и линии равного потенциала. На рис 7.17 изображена примерная картина расположения линий тока и линий равного потенциала при обтекании цилиндра. В силу симметрии изображена лишь верхняя половина течения.
и r, а затем построить линии тока. Аналогично строятся и линии равного потенциала. На рис 7.17 изображена примерная картина расположения линий тока и линий равного потенциала при обтекании цилиндра. В силу симметрии изображена лишь верхняя половина течения.

Рис. 7.17
Из (7.6.9) видно, что полученное решение удовлетворяет граничным условиям для идеальной жидкости: при  Компоненты скорости
Компоненты скорости  и
и 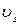 в любой точке поля течения вычисляются по формулам (7.6.9), а значение модуля скорости
в любой точке поля течения вычисляются по формулам (7.6.9), а значение модуля скорости  индивидуальной частицы может быть определено по формуле:
индивидуальной частицы может быть определено по формуле:
 (7.6.10)
(7.6.10)
На поверхности цилиндра  модуль скорости равен
модуль скорости равен  Очевидно, скорость имеет максимальное значение на поверхности цилиндра при углах
Очевидно, скорость имеет максимальное значение на поверхности цилиндра при углах 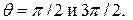 При этом абсолютное значение максимальной скорости равно
При этом абсолютное значение максимальной скорости равно  Из формулы (7.6.10) видно также, что в критических точках на поверхности цилиндра (q = 0, p) модуль скорости равен нулю.
Из формулы (7.6.10) видно также, что в критических точках на поверхности цилиндра (q = 0, p) модуль скорости равен нулю.
Подбирая соответствующее конформное отображение  , можно из простейшей задачи обтекания пластинки получить, например, обтекание эллипса, некоторого профиля крыла и других плоских тел, имеющих более сложную форму. В такой математической формализации и заключается эффективность применения теории функций комплексного переменного к решению задач о плоском, потенциальном движении идеальной жидкости.
, можно из простейшей задачи обтекания пластинки получить, например, обтекание эллипса, некоторого профиля крыла и других плоских тел, имеющих более сложную форму. В такой математической формализации и заключается эффективность применения теории функций комплексного переменного к решению задач о плоском, потенциальном движении идеальной жидкости.
Дата добавления: 2015-08-03; просмотров: 116 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обтекание плоской пластинки идеальной несжимаемой жидкостью | | | Парадокс Даламбера |