
|
Читайте также: |
Вычислим силу, действующую на единицу длины цилиндра со стороны движущейся среды Для этого вычислим распределение давления по его по-
верхности. Воспользуемся уравнением Бернулли для какой-либо линии тока
 . (7.6.11)
. (7.6.11)
Для линии тока, идущей по поверхности цилиндра (r = r 0), с учетом
(7.6. 9) квадрат скорости в любой точке на поверхности цилиндра равен
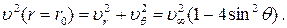 (7.6.11а)
(7.6.11а)
Из (7.6.11) следует распределение давления в любой точке поля течения около цилиндра P (r) и на его поверхности цилиндра P (r = r 0):
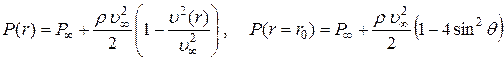 . (7.6.12)
. (7.6.12)
Из формулы (7.6.12) видно, что давление максимально при углах q = 0 и p (см. рис.7.18), т.е. в критических точках А (180°) и В(0°), и равно  (как это и следовало ожидать для точек полного торможения потока).
(как это и следовало ожидать для точек полного торможения потока).
Давление P в точках С и D на поверхности цилиндра равно давлению в набегающем потоке  при условии:
при условии:

т.е. в точках С (150°) и D (30°)  (см.рис.7.18). Если для наглядности
(см.рис.7.18). Если для наглядности
вдоль радиусов, проведённых из центра полукруга под различными углами q, отложить величину  , принимая её положительной и направленной по нормали к внешней стороне поверхности на интервалах 0 < q < 300 и 150 < q < 1800, а на интервале 30 < q < 1500 - отрицательной и направленной по нормали к внутренней стороне поверхности, то получим эпюру распределения относительной разности давлений, изображенную на рис.7.18.
, принимая её положительной и направленной по нормали к внешней стороне поверхности на интервалах 0 < q < 300 и 150 < q < 1800, а на интервале 30 < q < 1500 - отрицательной и направленной по нормали к внутренней стороне поверхности, то получим эпюру распределения относительной разности давлений, изображенную на рис.7.18.
Таким образом, на участках АС и ВД единичные площадки на поверхности испытывают сжатие под действием сил давления, а на участке СД - растяжение, т.е. силы давления, действующие на поверхность цилиндра, стремятся
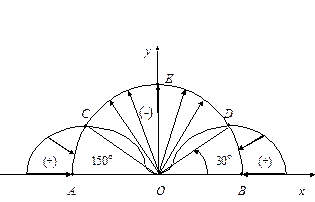 Рис.7.18 Рис.7.18
| деформировать (растянуть) его вдоль оси, перпендикулярной набегающему потоку. Если бы для измерения скорости воспользоваться цилиндром вместо трубки Пито, то отверстие, которое должно воспринимать давление в набегающем потоке вдали от тела, должно быть сделано в одной из точек  или или  . .
|
Вычислим силу F, с которой поток идеальной среды действует на единицу длины цилиндра в направлении оси z, перпендикулярной скорости набегающего потока, или силу лобового сопротивления. Для этого достаточно просуммировать силы давления, действующие на элементы поверхности цилиндра. По определению (3.2.1) имеем:
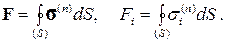
Но для идеальной среды  . Если ось i совпадает с осью x, то сила лобового сопротивления Fx равна:
. Если ось i совпадает с осью x, то сила лобового сопротивления Fx равна:
 (7.6.13)
(7.6.13)
Данный результат и составляет содержание парадокса Даламбера. Полученный вывод справедлив не только для цилиндра, но и для тела произвольной формы. При обтекании тел идеальной несжимаемой средой, если движение среды потенциально, сила лобового сопротивления равна нулю. Из симметрии движения очевидно, что и подъёмная сила  также равна нулю,
также равна нулю,
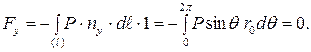 (7.6.14)
(7.6.14)
Этот удивительный результат был предметом длительной дискуссии Даламбера и Эйлера. Даламбер говорил в 1744 г.: «Странный парадокс, объяснение которого предоставляю математикам». Слово «парадокс» (по-гречески неожиданный) в науке означает неожиданное явление, не соответствующее обычным представлениям. Объясняя этот парадокс, русский ученый Эйлер предполагал в 1755 г., что реальная жидкость не похожа на идеальную. Эйлер писал: «Если некоторые люди увлекутся и будут думать, что можно продвигать тела через жидкость, не встречая сопротивления, т.к. сила, с которой жидкость действует на переднюю часть тела, будет уничтожаться действием такой же силы на заднюю часть, что не имеет места при движении действительных жидкостей, то такой вывод будет неправилен». Уже в то время Эйлер отмечал влияние трения реальных жидкостей на происхождение сопротивления тел. Таким образом, парадокс Даламбера не должен иметь места при движении реальных, хотя бы и маловязких жидкостей.
В каких случаях идеальной жидкости парадокс Даламбера не имеет места?
1. В общем случае сила сопротивления может возникать при движении тела в идеальной среде с разрывом скоростей на некоторых поверхностях, отходящих от поверхности обтекаемого тела. Так, при обтекании цилиндра модель идеальной среды допускает существование за телом некоторой застойной зоны неподвижной среды, ограниченной линиями АВ и СD разрыва скорости (рис. 7.19).
 Рис. 7. 19 Рис. 7. 19
| Очевидно, что для существования застойной зоны идеальной среды давление в ней должно быть однородным и равным неизменному давлению вдоль линий разрыва АС на рис.7. 19. Тогда давление в застойной зоне должно быть равно давлению на поверхности тела в точке возникновения разрыва А или С. Но, как следует из предыдущего параграфа давление в точке А или С меньше давления в любой точке передней |
части обтекаемого тела. Поэтому сила, с которой среда действует на переднюю часть тела, больше, чем сила, действующая на его заднюю часть, т.е. возникает некоторая сила сопротивления. Этот прием, т.е. рассмотрение некоторых разрывных течений идеальной жидкости, используется при вычислении подъемной силы и силы сопротивления крыла самолета, а также в других задачах гидродинамики.
2. Парадокс Даламбера не имеет места при движениях тела в среде с образованием волны. Например, при движении частично погруженного тела на поверхности среды, находящейся в поле тяжести, образуются волны, которые являются источниками так называемого волнового сопротивления.
3. Парадокс Даламбера отсутствует и при движении тела со сверхзвуковыми скоростями в сжимаемой идеальной среде, когда в ней образуются ударные волны (см. раздел «Газовая динамика»).
Дата добавления: 2015-08-03; просмотров: 186 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обтекание цилиндра идеальной несжимаемой жидкостью | | | Обтекание бесконечного цилиндра с циркуляцией |