Читайте также:
|
• Основное уравнение динамики идеальной жидкости (уравнение Эйлера):
р d v/dt = f - Vp, (1.7a)
где р — плотность жидкости, f - объемная плотность массовых сил (в случае силы тяжести f = pg), Vp — градиент давления.
• Уравнение Бернулли. В стационарном потоке идеальной жидкости вдоль
любой линии тока
р u2/2 + p gh +p = const. (1.76)
• Сила трения между двумя слоями жидкости:
где t) — вязкость жидкости.
• Формула Пуазейля. Поток жидкости через поперечное сечение трубы (в единицах мэ/с)
где R и / — радиус и длина трубы, P\~Pi ~ разность давлений на ее концах.
• Число Рейнольдса, определяющее характер течения вязкой жидкости:
где / — некоторый характерный размер.
* Формула Стокса. Сила сопротивления движению шарика радиусом г в вязкой жидкости:
| V-/ |
| Рис- |
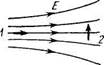
1367. Идеальная жидкость течет по
плоской трубе одинакового сечения,
расположенной в горизонтальной плос
кости и изогнутой, как показано на
рис. 1.76 (вид сверху). Поток стацио
нарный. Одинаковы ли давления и
скорости жидкостей в точках / и 2?
Какой вид имеют линии тока?
1368. Две манометрические трубки
установлены на горизонтальной трубе
переменного сечения в местах, где
сечения трубы равны St и 52
(рис. 1.77). По трубе течет вода. Найти объем воды, протекающий в единицу времени через сечение трубы, если разность уровней воды в манометрических трубках равна ДА.
 |  |
|
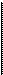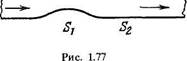
Рис. 1.78
1369. Трубка Пито (рис. 1.78) установлена по оси газопрово
да, площадь внутреннего сечения которого равна S. Пренебре
гая вязкостью, найти объем газа, проходящего через сечение
трубы в единицу времени, если разность уровней в жидкостном
манометре равна ДА, а плотность жидкости и газа — соответ
ственно р0 и р.
1370. Вертикальная струя идеальной жидкости вытекает из
горизонтального отверстия радиуса г0 со скоростью v0. Найти
радиус струи на расстоянии А ниже отверстия.
1371. Идеальная жидкость течет стационарным потоком по
наклонной плоскости. Глубина потока уменьшается в т] = 2,0 ра
за на расстоянии /. На каком расстоянии V глубина потока
уменьшится в ц' = 4,0 раза.
, 1372. На столе стоит широкий цилиндрический сосуд высоты А = 50 см. Сосуд наполнен водой. Пренебрегая вязкостью, найти, на какой высоте от дна сосуда следует сделать небольшое отверстие, чтобы струя из него била в поверхность стола на максимальное расстояние 1МХС от сосуда. Чему равно /макс?
| I |
| Рис. 1.79 |
1373. Какую работу необходимо совершить, чтобы, действуя посто-=? янной силой на поршень (рис. 1.79), выдавить из горизонтально расположенного цилиндра всю воду за время t? Объем воды в цилиндре равен V, площадь сечения отверстия s, причем s значительно меньше площади поршня. Трение и вязкость пренебрежимо малы.
1374. Из отверстия в дне высокого цилиндрического сосуда вытекает вода. Площадь сечения сосуда в ц = 100 раз больше сечения отверстия. Найти ускорение, с которым перемещается уровень воды в сосуде.
1375. Цилиндрический сосуд высоты h с площадью
основания S наполнен водой. В дне сосуда открыли отверстие
площадью s«S. Пренебрегая вязкостью воды, определить,
через сколько времени вся вода вытечет из сосуда.
1376. Тонкостенный цилиндрический сосуд погрузили в
идеальную жидкость до верхнего (открытого) основания. В
нижнем, закрытом торце имеется малое отверстие. Известны
высота сосуда А, а также отношение ц площади сечения
отверстия к площади сечения сосуда, причем ц« 1. Найти
время, за которое наполнится сосуд.
1377. Горизонтально рас
положенная трубка АВ дли- д g
ны / вращается с постоян
ной угловой скоростью со
вокруг неподвижной верти- ^ ~*
кальной оси О, проходящей
через конец А (рис. 1.80). В Рис- 1В0
трубке находится идеальная
жидкость. Конец А трубки открыт, а в закрытом конце В
имеется очень малое отверстие. Найти, с какой скоростью
относительно трубки будет вытекать жидкость в зависимости от
"высоты" ее столба А.
1378. Показать, что в случае стационарного потока идеаль
ной жидкости уравнение (1.7а) приводит к уравнению Бернулли.
1379. С противоположных сторон широкого вертикального
сосуда, наполненного водой, открыли два одинаковых отвер
стия, каждое площадью 5 = 0,50 см2. Расстояние между ними по
высоте ДА = 51 см. Найти результирующую силу реакции
вытекающей воды.
1380. В боковой стенке широкого цилиндрического верти
кального сосуда высоты А = 75 см сделана узкая вертикальная
щель, нижний конец которой упирается в дно сосуда. Длина
щели / = 50 см, ширина Ь = 1,0 мм. Закрыв щель, сосуд
наполнили водой. Найти результирующую силу реакции
вытекающей воды непосредственно после того, как щель
открыли.
1381. Вода течет со скоростью v по U-образной трубке,
лежащей в горизонтальной плоскости. Площадь сечения трубки
S, радиус закругления R. Найти:
а) суммарный импульс воды в закругленной части трубки;
б) модуль силы, действующей со стороны текущей воды на
стенки изогнутой части трубки.
| Рис. 1.81 |
1382. Вода вытекает из большого бака по изогнутой под прямым углом трубке, внутренний радиус которой г = 0,50 см (рис. 1.81). Длина горизонтальной части трубки / = 22 см. Расход воды Q = 0,50 л/с. Найти момент сил реакции воды на стенки этой трубки относительно точки О, обусловленный течением воды.
1383. Сечение ствола гидромонитора (рис. 1.82) меняется
| V///A |
| Рис. 1.82 |
от ^ = 50 см2 до 52 = 5,0 см2. Найти модуль и направление горизонтальной силы, возникающей в креплении ствола (сечение 1), если скорость струи на выходе v0 = 25 м/с. Вязкостью пренебречь.
1384. Цилиндрический сосуд с водой вращают вокруг его
вертикальной оси с угловой скоростью <о. Найти:
а) форму свободной поверхности воды;
б) распределение давления воды на дне сосуда вдоль его
радиуса, если давление в центре дна равно р0.
1385. Тонкий горизонтальный диск радиуса Я = 10 см рас
положен в цилиндрической полости с маслом, вязкость
| SCO |
которого т] = 8мПас (рис. 1.83). Зазоры между диском и горизонтальными торцами полости одинаковы и равны Л = 1,0 мм.
у уу_ ,. - Найти мощность, которую раз-
| Рис. 1.83 |
У///////////////////////////////////У/ вивают силы вязкости, действующие на диск при вращении его с w =60 рад/с. Краевыми эффектами пренебречь.
1386. Длинный цилиндр радиуса Rx перемещают вдоль его
оси с постоянной скоростью v0 внутри коаксиального с ним
неподвижного цилиндра радиуса £j. Пространство между
цилиндрами заполнено вязкой жидкостью. Найти скорость
жидкости как функцию расстояния г от оси цилиндров.
Течение ламинарное.
1387. Жидкость с вязкостью т\ находится между двумя
длинными коаксиальными цилиндрами с радиусами R, и R-,
причем Rl<R2. Внутренний цилиндр неподвижен, а внешний вращают с угловой скоростью ы2. Движение жидкости ламинарное. Имея в виду, что сила трения, действующая на единицу площади цилиндрической поверхности радиуса г, равна а = т)г (ды/дг), найти:
а) угловую Скорость вращающейся жидкости как функцию
радиуса г;
б) момент сил трения, действующих на единицу длины
внешнего цилиндра.
1388. По трубе радиуса R течет стационарный поток вязкой
жидкости. На оси трубы ее скорость равна v0. Найти скорость
жидкости как функцию расстояния г от оси трубы.
1389. По трубе длины / и радиуса R течет стационарный
поток жидкости, плотность которого р и вязкость т). Скорость
течения жидкости зависит от расстояния г до оси трубы как
v=vo(l -r2/R2). Найти:
а) объем жидкости, протекающий через сечение трубы
ежесекундно;
б) кинетическую энергию жидкости в объеме трубы;
в) разность давлений на концах трубы.
1390. Жидкость, плотность которой р и вязкость т), те
чет плоским стационарным потоком по наклонной плоскости,
составляющей угол а с горизонтом. Толщина потока равна h.
Найти объем жидкости, протекающей за единицу времени через
поперечное сечение потока в расчете на единицу его ширины.
1391. В системе (рис. 1.84) из широкого сосуда А по трубке
вытекает вязкая жидкость, плотность которой р = 1,0 г/см3.
Найти скорость вытекающей жидкости, если hx = 10 см,
А2 = 20 см и А3 = 35см. Расстояния I одинаковы.
| —Т ----- 71. | i 1 | i |
| hz | ||
| Е/1Е.- | ||
| —-- |
\\\
Рис. 1.84
1392. Радиус сечения трубопровода монотонно уменьшается
по закону г = гое"вх, где а = 0,50 м"1, х — расстояние от начала трубопровода. Найти отношение чисел Рейнольдса в сечениях, отстоящих друг от друга на Дх = 3,2 м.
1393. При движении шарика радиуса тг = 1,2 мм в глицерине
ламинарное обтекание наблюдается при скорости шарика, не
превышающее Uj = 23cm/c. При какой минимальной скорости
v2 шара радиуса г2 = 5,5 см в воде обтекание станет турбулентным? Вязкости глицерина и воды равны соответственно
tij= 1,39 Пас и ц2= 1,1 мПа-с.
1394. Свинцовый шарик равномерно опускается в глицерине,
вязкость которого т) = 1,39 Па*с. При каком наибольшем
диаметре шарика его обтекание еще ламинарное? Переход к
турбулентному обтеканию соответствует числу Re = 0,5 (это
значение Re, при котором за характерный размер взят диаметр
шарика).
1395. Стальной шарик диаметра d = 3,0 мм опускается с
нулевой начальной скоростью в прованском масле, вязкость
которого т]=90мПас. Через сколько времени после начала
движения скорость шарика будет отличаться от установившего
ся значения на л = 1,0%?
1.8. Релятивистская механика
* Лоренцево сокращение длины и замедление хода движущихся часов:
-. (1
/l - (We)2
где Ц — собственная длина, Дс0 — собственное время движущихся часов. • Преобразования Лоренца:
| У'У |
. f. jzxgcL. (1.8б)
\Д - (У/с)2 й-(У1с?
• Интервал sn — инвариантная величина:
где t12 — промежуток времени между событиями 1 и 2, 1п — расстояние между точками, где произошли эти события.
* Преобразование скорости:
v-V,
и = v = —'
' l-uxV/c2 ' l-vxVlc2
• Релятивистский импульс:
где»!,.=----------- — релятивистская масса, m — масса (покоя).
Vi - («/<о2
• Релятивистское уравнение динамики частицы:
где j> — релятивистский импульс частицы.
• Полная и кинетическая энергии релятивистской частицы:
Е = тгс2 = тс2 + К, К = (тг-т)с2.
• Связь между энергией и импульсом релятивистской частицы:
• При рассмотрении столкновения частиц полезно использовать инвариантную величину:
£2-/>V = mV, (1.8и)
где Е и р — полная энергия и импульс системы до столкновения, т — масса образовавшейся частицы (или системы).
1396. Стержень движется в продольном направлении с
постоянной скоростью v относительно инерциальнои Х-системы
отсчета. При каком значении v длина стержня в этой системе
отсчета будет на т) = 0,50 % меньше его собственной длины?
1397. Имеется прямоугольный треугольник, у которого катет
а = 5,00 м и угол между этим катетом и гипотенузой а = 30°.
Найти в системе отсчета К', движущейся относительно этого
треугольника со скоростью v =0,866 с вдоль катета а:
а) соответствующее значение угла а';
б) длину /' гипотенузы и ее отношение к собственной
длине.
1398. Найти собственную длину стержня, если в А^-системе
отсчета его скорость v=cj2, длина £ = 1,00 м и угол между ним
и направлением движения д = 45°.
1399. Стержень движется равномерно в продольном
направлении мимо двух меток А и В, расположенных на
расстоянии Ах друг от друга. Сначала в момент гх напротив
метки А оказался передний конец стержня. Затем напротив
метки В в моменты t2 и f3 оказались соответственно передний
и задний концы стержня. Найти его собственную длину.
1.400. С какой скоростью двигались в А^-системе отсчета
часы, если за время t = 5,0 с (в Х-системе) они отстали от
часов этой системы на Д* = О,1Ос?
1.401. Стержень пролетает с постоянной скоростью мимо
метки, неподвижной в А'-системе отсчета. Время пролета
At = 20 не в ^-системе. В системе же отсчета, связанной со
стержнем, метка движется вдоль него в течение Д/' = 25нс.
Найти собственную длину стержня.
1.402. Собственное время жизни некоторой нестабильной
частицы Дго=10нс. Какой путь пролетит эта частица до
распада в лабораторной системе отсчета, где ее время жизни
Д* = 20 не?
1.403. В /^-системе отсчета мюон, движущийся со скоростью
v =0,990 с, пролетел от места своего рождения до точки
распада расстояние / = 3,0 км. Определить:
а) собственное время жизни этого мюона;
б) расстояние, которое пролетел мюон в А~-систсме отсчета
с "его точки зрения".
1.404. Две частицы, двигавшиеся в лабораторной системе
отсчета по одной прямой с одинаковой скоростью и = Зс/4,
попали в неподвижную мишень с промежутком времени
Д* = 50нс. Найти собственное расстояние между частицами до
попадания в мишень.
1.405. Стержень движется вдоль линейки с некоторой по
стоянной скоростью. Если зафиксировать положение обоих кон
цов данного стержня одновременно в системе отсчета, связан
ной с линейкой, то разность отсчетов по линейки A*j = 4,0 м.
Если же положение обоих концов зафиксировать одновременно
в системе отсчета, связанной со стержнем, то разность отсчетов
по этой же линейке Ajc2 = 9,0m. Найти собственную длину
стержня и его скорость относительно линейки.
1.406. Два стержня одинаковой собственной длины /0
движутся навстречу друг другу параллельно общей горизонталь
ной оси. В системе отсчета, связанной с одним из стержней,
промежуток времени между моментами совпадения левых и
правых концов стержней оказался равным Д*. Какова скорость
одного стержня относительно другого?
1.407. Две нестабильные частицы движутся в А"-системе
отсчета по некоторой прямой в одном направлении со
скоростью v = 0,990 с. Расстояние между ними в этой системе
отсчета / = 120м. В некоторый момент обе частицы распались
одновременно в системе отсчета, связанной с ними. Какой
промежуток времени между моментами распада обеих частиц
наблюдали в А-системе? Какая частица распалась позже в ЛГ-системе?
1.408. Стержень А В, ориентированный вдоль оси х /^-систе
мы отсчета, движется с постоянной скоростью v в положитель
ном направлении оси х. Передним концом стержня является
точка А, задним — точка В. Найти:
а) собственную длину стержня, если в момент ХА координа
та точки А равна хл, а в момент tB координата точки В
равна хв;
б) через какой промежуток времени надо зафиксировать
координаты начала и конца стержня в ^-системе, чтобы
разность координат оказалась равной собственной длине
стержня.
1.409. Стержень А'В' движется а' В'
с постоянной скоростью v отно- Q ^
сительно стержня АВ (рис. 1.85).
Оба стержня имеют одинаковую
собственную длину /0 и на кон- Рис- 185
цах каждого из них установлены
синхронизированные между собой часы: А с В и А' с В'.
Пусть момент, когда часы В' поравнялись с часами А, взят
за начало отсчета времени в системах отсчета, связанных с
каждым из стержней. Определить:
а) показания часов В и В' в момент, когда они окажутся
напротив друг друга;
б) то же для часов А и А'.
1.410. Имеются две группы синхронизированных часов 1С и
К', движущихся одна относительно другой со скоростью и, как
показано на рис. 1.86. Возьмем за начало отсчета времени мо
мент, когда часы А' окажутся напротив часов А. Изобразить
примерное расположение стрелок всех часов в этот момент с
"точки зрения" Х-часов; К '-часов.
оо©оо
к1
Рис. 1.86
1.411. if'-система отсчета движется в положительном направ
лении оси х iC-системы со скоростью V относительно послед
ней. Пусть в момент совпадения начал координат О и О'
показания часов обеих систем в этих точках равны нулю.
Найти в ^-системе скорость х перемещения точки, в которой
показания часов обеих систем отсчета будут все время
одинаковы. Убедиться, что x<V.
1.412. В двух точках iC-системы произошли события,
разделенные промежутком времени At. Показать, что если эти
события причинно связаны в iC-системе (например, выстрел и
попадание в мишень), то они причинно связаны и в любой
другой инерциальной К '-системе отсчета).
| Ct,M б |
| В | |||||||
| С | |||||||
| А | |||||||
1.413. На диаграмме пространство - время (рис. 1.87) показаны три события А, В и С, которые произошли на оси х некоторой инерциальной системы отсчета. Найти:
а) промежуток времени между событиями А и В
в той системе отсчета, где оба события произошли в одной точке;
| О 1 2 3 4 5 6 7 х,м |
б) расстояние между точками, где произошли
| Рис. 1.87 |
события Л и С, в той системе отсчета, где они одновременны.
1.414. В плоскости ху iC-системы отсчета движется частица,
проекции скорости которой равны vx и и. Найти скорость и'
этой частицы в.К'-системе, которая перемещается со скоростью
V относительно ^-системы в положительном направлении ее
оси х.
1.415. Две частицы движутся навстречу друг другу со
скоростями Uj = O,5Oc и v2 = 0,75c по отношению к лаборатор
ной системе отсчета. Найти:
а) скорость, с которой уменьшается расстояние между
частицами в лабораторной системе отсчета;
б) относительную скорость частицы.
1.416. Два стержня одинаковой собственной длины 10
движутся в продольном направлении навстречу друг другу па
раллельно общей оси с одной и той же скоростью v относи-
тельно лабораторной системы отсчета. Чему равна длина каждого стержня в системе отсчета, связанной с другим стержнем?
1.417.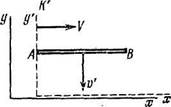 
Две релятивистские частицы движутся под прямым
углом друг к другу в лабораторной системе отсчета, причем
одна со скоростью vt, а другая со скоростью v2. Найти их
относительную скорость.
1.418. Некоторая нестабильная частица движется со ско
ростью i/ в К '-системе отсчета вдоль ее оси у'.. К'-система в
свою очередь перемещается относительно iC-системы со
скоростью V в положительном направлении ее оси х. Оси х'
и х обеих систем отсчета совпадают, оси у' и у параллельны
друг другу. Найти путь, который частица пролетит в ^-системе,
если ее собственное время жизни равно Д»о.
1.419. Частица движется в А"-системе со скоростью и под
углом Ь к оси х. Найти соответствующий угол в ^'-системе,
перемещающейся со скоростью V относительно iC-системы в
положительном направлении ее оси х, если оси х и х' обеих
систем совпадают.
1.420. Стержень А В ориенти- К
рован параллельно оси х'. К'-сис
темы отсчета и движется в этой
системе со скоростью v' вдоль
ее оси у'. А"'-система в свою
очередь движется со скоростью V
относительно ^-системы, как
показано на рис. 1.88. Найти
угол Ь между стержнем и осью Рис- 188
х в iC-системе.
1.421..К'-система перемещается с постоянной скоростью V
относительно Х-системы. Найти ускорение а' частицы в
if'-системе, если в iC-системе она движется со скоростью v и
ускорением а по прямой:
а) в направлении вектора V;
б) перпендикулярно вектору V.
1.422. Стартовавшая с Земли воображаемая космическая
ракета движется с ускорением a' = 10g, одинаковым в каждой
инерциальной системе, мгновенно сопутствующей ракете. Разгон
продолжался по земному времени х = 1,0 год. Найти, на сколько процентов отличается скорость ракеты от скорости света в конце разгона. Каков путь, пройденный ракетой к этому моменту?
1.423. Используя данные предыдущей задачи, определить
время разгона ракеты х0 в системе отсчета, связанной с самой
Т
ракетой. Иметь в виду, что T0=J\/l -(v/c)2dt, где х - время
О
разгона в системе Земли.
1.424. Во сколько раз релятивистская масса частицы,
скорость которой отличается от скорости света на ц= 0,010 %,
превышает ее массу покоя?
1.425. Плотность покоящегося тела равна р0. Найти
скорость системы отсчета относительно данного тела, в которой
его плотность будет на tj = 25% больше р0.
1.426. Протон движется с импульсом р = 10,0 ГэВ/с, где с -
скорость света. На сколько процентов отличается скорость этого
протона от скорости света?
1.427. Найти скорость при которой релятивистский импульс
частицы в г\ = 1,4 раза превышает ее ньютоновский импульс.
1.428. Какую работу надо совершить, чтобы увеличить
скорость частицы с массой т от 0,60 с до 0,80с? Сравнить
полученный результат со значением, вычисленным по нереля
тивистской формуле.
1.429. При какой скорости кинетическая энергия частицы
равна ее энергии покоя?
1.430. При каких значениях отношения кинетической
энергии частицы к ее энергии покоя относительная погреш
ность при расчете ее скорости по нерелятивистской формуле
не превышает ti = 0,010?
1.431. Найти зависимость импульса частицы с массой т от
ее кинетической энергии. Вычислить импульс протона с
кинетической энергией 500 МэВ.
1.432. Найти скорость частицы, кинетическая энергия
которой К = 500 МэВ и импульс р = 865 МэВ/с, где с - скорость
света.
1.433. Пучок релятивистских частиц с кинетической энергаеи
К падает на поглощающую мишень. Сила тока в пучке равна
/, заряд и масса каждой частицы равны е и т. Найти силу
давления пучка на мишень и выделяющуюся в ней мощность.
1.434. Сколько энергии (в расчете на единицу массы)
необходимо затратить, чтобы сообщить первоначально покоив
шемуся космическому кораблю скорость и =0,980 с?
1.435. Частица массы т в момент t = 0 начинает двигаться
под действием постоянной силы F. Найти скорость частицы
и пройденный ею путь в зависимости от времени г.
1.436. Частица массы т движется вдоль оси х А'-системы
отсчета по закону х = <Jd2 + c2t2, где d - некоторая постоянная, с - скорость света, t - время. Найти силу, действующую на частицу в этой системе отсчета.
1.437. Исходя из уравнения (1.8е), найти:
а) в каких случаях ускорение частицы совпадает по
направлению с действующей на нее силой F;
б) коэффициенты пропорциональности между силой F и
ускорением а, когда Fxv и F||v, где v - скорость частицы.
1.438. Релятивистская частица с импульсом р и полной
энергией Е движется вдоль оси х А'-системы отсчета. Показать,
что в А"'-системе, движущейся с постоянной скоростью V
относительно А'-системы в положительном направлении ее оси
х, импульс и полная энергия данной частицы определяются
формулами (Р = V/c)
1.439. Энергия фотона в Х-системе отсчета равна е.
Воспользовавшись формулами преобразования, проведенными
в предыдущей задаче, найти энергию е' этого фотона в
А"'-системе, перемещающейся со скоростью V относительно
А'-системы в направлении движения фотона. При каком
значении V энергия е'=е/2?
1.440. Показать, что величина Е2-р2сг есть инвариант, т.е.
имеет одно и то же значение во всех инерциальных системах
отсчета. Каково значение этого инварианта?
1.441. Две частицы, каждая массы т, летят навстречу друг
другу с одинаковой скоростью v. Найти v, если масса
образовавшейся при столкновении частицы равна М.
1.442. Нейтрон с кинетической энергией К = 2тс2, где т —
его масса, налетает на другой, покоящийся нейтрон. Найти в
системе их центра масс:
а) суммарную кинетическую энергию К нейтронов;
б) импульс р каждого нейтрона.
1.443. Релятивистская частица массы т с кинетической
энергией К налетает на покоящуюся частицу той же массы.
Найти массу и скорость составной частицы, образовавшейся в
результате соударения.
1.444. Какова должна быть кинетическая энергия протона,
налетающего на другой, покоящийся протон, чтобы их суммар-
ная кинетическая энергия в системе центра масс была такая же, как у двух протонов, движущихся навстречу друг другу с кинетическими энергиями К = 25,0 ГэВ?
1.445. Неподвижная частица массы т распадается на три
частицы масс /я,, т2, т3. Найти наибольшую полную энергию,
которую может иметь, например, частица т1.
1.446. Релятивистская ракета выбрасывает струю газа с
нерелятивистской скоростью и, постоянной относительно
ракеты. Найти зависимость скорости v ракеты от ее массы т,
если в начальный момент масса ракеты равна т0.
Часть 2 ЭЛЕКТРОМАГНЕТИЗМ
2.1. Постоянное электрическое поле в вакууме
• Напряженность и потенциал поля точечного заряда д:
E^-1-^r, <Р=-±-4. (2.1а)
4яе0 г3 4пг0 г
• Связь между напряженностью поля и потенциалом:
£,= -Э(р/Э/, E = -V(p. (2.16)
• Теорема Гаусса и циркуляция вектора Е:
• Потенциал и напряженность поля точечного диполя с электрическим моментом р:
<Р
4пг0 Гз 4л е0 г3
где в - угол между векторами г и р.
• Энергия W диполя р во внешнем электрическом поле и момент сил N,
действующих на диполь:
W=-pE, N = [pE]. (2-1д)
• Сила F, действующая на диполь, и ее проекция Fx:
F = рЭЪ/dl, FX =?VEX. (2. le)
где дВ/dl — производная вектора Е по направлению диполя.
2.1. Найти отношение электрической и гравитационной сил взаимодействия между двумя электронами; двумя протонами. При каком значении удельного заряда q/m частицы эти силы будут равными?
22. Два одинаковых небольших металлических шарика с зарядами q1 и q2 находясь на расстоянии / = 200 м друг от друга, притягиваются с силой F0 = 36mH. После того, как шарики привели в соприкосновение и опять развели на то же
расстояние I, они стали отталкиваться с силой F = 64mH. Найти qt и q2.
23. Два положительных заряда qt и q2 находятся в точках с радиусами-векторами rt и tj. Найти отрицательный заряд qi и радиус-вектор г3 точки, в которую его надо поместить, чтобы сила, действующая на каждый из этих трех зарядов, была равна нулю.
2.4. Три небольших одинаково заряженных шарика массы
от = 9,0 г подвешены к одной точке на шелковых нитях длины
/ = 250 м. Найти заряд каждого шарика, если углы между
разошедшимися нитями равны 2а = 60°.
2.5. Два небольших одинаково заряженных шарика массы
т = 5,0 г подвешены к одной точке на шелковых нитях,
образующих между собой малый угол 0, и находятся на одном
уровне. Найти скорость утечки заряда dq/dt с каждого шарика
в момент, когда ft = 5,0°, если скорость сближения шариков
постоянна и равна v =0,55 мм/с
2.6. Три небольших шарика, каждый массы то = 6,0 г и с
зарядом q = 1,0 мкКп, соединены шелковыми нитями, образуя
равносторонний треугольник со стороной / = 200 мм. Одну нить
пережгли. Найти ускорение среднего шарика сразу после этого.
Сил тяжести нет.
2.7. Тонкое проволочное кольцо радиуса R = 100 мм имеет
электрический заряд ^ = 50мкКл. Каково будет приращение
силы, растягивающей проволоку, если в центре кольца помес
тить точечный заряд qQ = 7,0 мкКл?
2.8. Положительный точечный заряд 50 мкКл находится на
плоскости ху в точке с радиусом-вектором ro = 2i + 3j, где i и
j - орты осей х и у. Найти напряженность электрического
поля и ее модуль в точке с радиусом-вектором r = 8i-5j. Здесь
г0 и г даны в метрах.
2.9. В вершинах квадрата с диагональю 2/ = 100 мм находятся
одинаковые по модулю (#=2,5мкКл) точечные заряды, знаки
которых при обходе квадрата расположены в порядке +, +,
—, -. Найти напряженность Е электрического поля в точке, отстоящей на расстояние х = 50 мм от центра квадрата и расположенной симметрично относительно его вершин.
2.10. Тонкий стержень А В длины / = 100 см имеет заряд
q = 37 нКл, распределенный так, что его линейная плотность
пропорциональна квадрату расстояния от конца А. Найти
напряженность электрического поля в точке А.
2.11. Тонкое полукольцо радиуса R = 20 см заряжено равно
мерно зарядом д = 0,70нКл. Найти модуль напряженности
электрического поля в центре кривизны этого полукольца.
2.12. Кольцо радиуса R из тонкой проволоки имеет заряд q.
Найти модуль напряженности электрического поля на оси
кольца как функцию расстояния I до его центра. Исследовать
Е(1) при I»R. Определить максимальное значение напряжен
ности и соответствующее расстояние I. Изобразить примерный
график функции Е(1).
2.13. Полубесконечный круглый цилиндр радиуса R заряжен
равномерно по поверхности так, что на единицу его длины
приходится заряд Я. Найти напряженность электрического поля в центре основания цилиндра.
2.14. Найти напряженность электрического поля в центре
основания полусферы, заряженной равномерно с поверхностной
плотностью а = 60 нКл/м2.
2.15. Плоскость с круглым отверстием радиуса R равномерно
заряжена с поверхностной плотностью а. Найти напряженность
Е электрического поля на оси отверстия как функцию расстоя
ния / до его центра.
2.16. Система состоит из тонкого заряженного проволочного
кольца радиуса R и очень длинной равномерно заряженной
нити, расположенной по оси кольца так, что один из ее концов
совпадает с центром кольца. Последнее имеет заряд q. На
единицу длины нити приходится заряд X. Найти силу взаимо
действия кольца и нити.
2.17. Тонкое непроводящее кольцо радиуса R заряжено с
линейной плотностью А = A0coscp, где Ао - постоянная, ср —
азимутальный угол. Найти модуль напряженности электрическо
го поля:
а) в центре кольца;
б) на оси кольца в зависимости от расстояния х до его
центра. Исследовать полученное выражение при x»R.
2.18. Находящийся в вакууме тонкий прямой стержень длины
2а заряжен равномерно зарядом q. Найти модуль напряженно
сти электрического поля как функцию расстояния г от центра
стержня до точки прямой,
а) перпендикулярной стержню и проходящей через его
центр;
б) совпадающий с осью стержня, если т>а.
Исследовать полученные выражения при г»а.
2.19. Длинная прямая равномерно заряженная нить имеет заряд А на единицу длины. Найти модуль и направление электрического поля в точке, которая отстоит от нити на расстояние у и находится на перпендикуляре к нити, проходящем через один из ее концов.
220. Равномерно заряженная нить, на единицу длины которой
приходится заряд X, имеет конфигурации, показанные на
рис. 2.1. Радиус закругления R
R значительно меньше длины нити.
" Воспользовавшись результатом
О 6 решения предыдущей задачи,
найти модуль напряженности
ис" ' электрического поля в точке О
для конфигураций а и б.
221. Сфера радиуса г заряжена с поверхностной плотностью
а = аг, где а — постоянный вектор, t — радиус-вектор точки
сферы относительно ее центра. Найти напряженность электри
ческого поля в центре сферы.
222. Поверхностная плотность заряда на сфере радиуса R
зависит от полярного угла Ь как о = er0 cos Ь, где <т0 - положи
тельная постоянная. Показать, что такое распределение заряда
можно представить как результат малого сдвига относительно
друг друга двух равномерно заряженных шаров радиуса R,
заряды которых одинаковы по модулю и противоположны по
знаку. Воспользовавшись этим представлением, найти напряжен
ность электрического поля внутри данной сферы.
2.23. Найти напряженность электрического поля в центре шара радиуса R, объемная плотность заряда которого р = аг, где а — постоянный вектор, t — радиус-вектор относительно центра шара.
224. Пространство между двумя плоскостями, отстоящими
друг от друга на расстояние 2а, заполнено зарядом, объемная
плотность которого зависит только от координаты х оси,
перпендикулярной этим плоскостям, как р = ах, где а -
постоянная. Начало координат (х = 0) находится посередине
между этими плоскостями. Найти зависимости от х напряжен
ности электрического поля, точнее Ех(х) и Е(х). Изобразить их
примерные графики.
225. Две длинные параллельные нити равномерно заряжены,
каждая с линейной плотностью Я = 0,50 мкКл/м. Расстояние
| О |
| R |
/7.
между нитями / = 45 см. Найти максимальное значение напряженности электрического поля в плоскости симметрии этой системы.
226. Две скрещивающиеся взаимно перпендикулярные нити бесконечной длины заряжены равномерно с линейной плотностью Я. Найти силу их взаимодействия.
2.27. Бесконечно длинная цилиндрическая поверхность
круглого сечения заряжена равномерно по длине с поверхнос
тной плотностью о = а0 cos ср, где ср - полярный угол цилин
дрической системы координат, ось z которой совпадает с осью
данной поверхности. Найти модуль и направление напряженнос
ти электрического поля на оси г.
2.28. Грани полого куба заряжены равномерно с поверхнос
тной плотностью а. Найти силу, которая действует на каждую
грань со стороны:
а) точечного заряда q, если его поместить в центр куба;
б) остальных граней, если ребро куба равно /.
229. Имеется аксиально-симметричное электрическое поле,
напряженность которого зависит от расстояния г до его оси как Е = аг/г2, где а — постоянная. Найти заряд внутри сферы радиуса R с центром на оси этого поля.
2-30. Напряженность электрического поля В = агт, где а -постоянная, г - расстояние от центра поля. Найти плотность зарядов р (г), создающих это поле.
231. Шар радиуса R имеет положительный заряд, объемная
плотность которого зависит только от расстояния г до его
центра как р = р0 (1 - r/R), где р0 — постоянная. Пренебрегая
влиянием вещества шара, найти:
а) модуль напряженности электрического поля внутри и вне
шара как функцию г;
б) максимальное значение модуля напряженности £макс и
соответствующее ему значение rm.
232. Система состоит из шара радиуса R, заряженного
сферически-симметрично, и окружающей среды, заполненной
зарядом с объемной плотностью р = а/г, где а - постоянная,
г - расстояние от центра шара. Пренебрегая влиянием
вещества, найти заряд шара, при котором модуль напряженнос
ти электрического поля вне шара не зависит от г. Чему равна
эта напряженность?
233. Внутри шара, заряженного равномерно с объемной
плотностью р, имеется сферическая полость. Центр полости
смещен относительно центра шара на расстояние а. Пренебрегая влиянием вещества шара, найти напряженность Е поля внутри полости.
|
| Рис. 2.2 |
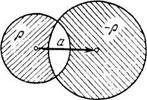
234. Найти напряженность Е элек
трического поля в области пересече
ния двух шаров, равномерно запо
лненных разноименными по знаку
зарядами с объемной плотностью р
и - р, если расстояние между центра
ми шаров равно а (рис. 2.2).
235. Три одинаковых шарика,
расположенные в вершинах равносто
роннего треугольника со стороной а,
соединены друг с другом нитями. Заряд и масса каждого шарика равны q и т. Одну из нитей пережгли. Найти максимальную скорость среднего шарика. Сил тяжести нет.
2.36. Имеются два тонких проволочных кольца радиуса R каждое, оси которых совпадают. Заряды колец равны q и -q. Найти разность потенциалов между центрами колец, отстоящими друг от друга на расстояние /, если R - 30 см, 7 = 52 см и q - 0,40 мкКл.
237. Бесконечно длинная прямая нить заряжена равномерно
с линейной плотностью Л = 0,40 мкКл/м. Вычислить разность
потенциалов точек 1 и 2, если точка 2 находится дальше от
нити, чем точка 1, в ц = 2,0 раза.
238. Тонкое кольцо радиуса R = 25 см имеет заряд q =
= 5,0 мкКл, неравномерно распределенный по кольцу. Найти
работу электрических сил при перемещении точечного заряда
q' = 10 мкКл из центра кольца по произвольному пути в точку,
находящуюся на оси кольца на расстоянии I = 50 см от его центра.
239. Круглая тонкая пластинка радиуса R равномерно
заряжена с поверхностной плотностью а. Найти потенциал и
модуль напряженности электрического поля на оси пластинки
как функцию расстояния I от ее центра. Рассмотреть также
случаи / - 0 и / » R.
2.40. Коническая поверхность с основанием радиуса R
равномерно заряжена с поверхностной плотностью а. Найти
потенциал в вершине конуса.
2.41. Найти потенциал на краю тонкого диска радиуса
R = 20 см, по которому равномерно распределен заряд с
поверхностной плотностью а = 0,25 мкКл/м2.
2.42. Заряд q распределен равномерно по объему шара
радиуса R. Пренебрегая влиянием вещества шара, найти
потенциал:
а) в центре шара;
б) внутри шара как функцию расстояния г от его центра.
2.43. Найти напряженность электрического поля, потенциал
которого имеет вид ср = аг, где & - постоянный вектор, ж —
радиус-вектор точки поля.
2.44. Определить напряженность электрического ноля,
потенциал которого зависит от координат х, у по закону:
а) (р = а (х2-у2); б) <р = аху,
где а — постоянная. Изобразить примерный вид этих полей с помощью линий вектора Е (в плоскости ху),
2.45. Потенциал электрического поля имеет вид <р =
= a(xy~zl), где с - постоянная. Найти проекцию напряженно
сти электрического поля в точке М{2, 1, -3} на направление
вектора a = i + 3k.
2.46. Показать, что потенциал поля диполя с электрическим
моментом р (рис. 2.3) может быть представлен как <р = рг/4яеог*,
где г — радиус-вектор. Найти с помощью этого выражения модуль напряженности электрического ноля диполя как функцию г и Ь.
| Рыс 2з |
|
| Рис. 2.4 |
| а(2х-1), где а - |
2.47. Точечный электрический диполь с
моментом р находится во внешнем одно
родном электрическом поле, напряженность
которого равна Ео, причем рИЕ0. В этом
случае одна из эквипотенциальных повер
хностей, охватывающих диполь, является
сферой. Найти ее радиус.
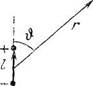
2.48. Две параллельные тонкие нити
равномерно заряжены с линейной плот
ностью А и -А. Расстояние между нитями
/. Найти потенциал и модуль напряженнос
ти электрического поля на расстоянии
г» I под углом Ь к вектору I (рис. 2.4).
2.49. Найти электрический момент р
тонкого стержня длины /, линейная илот-
ность заряда которого зависит от расстоя
ния х до одного из его концов как \ =
положительная постоянная.
|
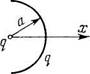
2.50. Система состоит из заряда q>0, равномерно распределенного по полуокружности радиуса а, в центре которой находится точечный заряд -q (рис. 2.5). Найти:
а) электрический дипольный момент этой
системы;
| Рис. 2.5 |
б) модуль напряженности электрического
поля на оси х системы на расстоянии г»а
от нее.
| Рис. 2.6 |
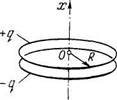2.51. Два коаксиальных кольца радиуса R из тонкой проволоки находятся на малом расстоянии I друг от друга (/«R) и имеют заряды q и -q. Найти потенциал и напряженность электрического поля на оси системы как функции координаты х (рис. 2.6). Изобразить примерные графики этих зависимостей. Исследовать эти
функции при |*|» Я.
|
| Рис. 2.7 |
2.52. Какую работу против сил электричес
кого поля надо совершить, чтобы перенести
диполь с электрическим моментом р из
положения 1, где напряженность поля равна
Ех, в положение 2 с напряженностью Е2
(рис. 2.7)?
2.53. Диполь с электрическим моментом
р находится на расстоянии г от длинной
прямой нити, заряженной равномерно с линейной плотностью Я. Найти силу F, действующую на диполь, если вектор р ориентирован:
а) вдоль нити;
б) по радиусу-вектору г;
в) перпендикулярно нити и радиусу-вектору t.
2.54. Найти силу взаимодействия двух молекул воды,
отстоящих друг от друга на / = 10 нм, если их электрические
моменты расположены вдоль одной и той же прямой. Момент
каждой молекулы р = 0,62 • 1<Г29 Клм.
2.55. Найти потенциал следующих электрических полей:
а) E = a(yi+xj);
б) E = 2axyi + a(x2-y2)j;
в) Е = ау\ + (ах + bz)j + byk.
Здесь а и Ь - постоянные, i, j, k - орты осей х, у, z.
2.56. Потенциал поля в некоторой области пространства
зависит только от координаты х как ф = -ах3 + Ь, где а и Ь — некоторые постоянные. Найти распределение объемного
заряда р(х).
2.57. Между двумя большими параллельными пластинами,
отстоящими друг от друга на расстояние d, находится равно
мерно распределенный объемный заряд. Разность потенциалов
пластин равна Дер. При каком значении объемной плотности
р заряда напряженность поля вблизи одной из пластин будет
равна нулю? Какова будет при этом напряженность поля у
другой пластины?
2.58. Потенциал поля внутри заряженного шара зависит
только от расстояния до его центра как ф = аг2 + Ь, где а и Ъ — постоянные. Найти распределение объемного заряда р (г) внутри шара.
Дата добавления: 2015-08-02; просмотров: 824 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Динамика твердого тела | | | Проводники и диэлектрики в электрическом поле |