Упругие волны. Акустика 3 страница

4.24. Трехгранная призма с преломляющим углом 60° дает угол наименьшего отклонения в воздухе 37°. Какой угол наименьшего отклонения даст эта призма в воде?

425. Луч света, содержащий две монохроматические
составляющие, проходит через трехгранную призму с преломля­
ющим углом 8 = 60". Определить угол Д а между обеими
составляющими луча после призмы, если показатели преломле­
ния для них равны 1,515 и 1,520 и призма ориентирована на
угол наименьшего отклонения.

426. Вывести с помощью принципа Ферма законы отраже­
ния и преломления света на плоской границе раздела.

427. Открытый сверху сосуд, на дне которого находится
точечный монохроматический источник света, заполняют снизу
водой так, что ее уровень поднимается со скоростью
v= 9,0 мм/с. Найти относительный сдвиг частоты А ы/w света,
который наблюдают над поверхностью воды вдоль вертикали,
проходящей через источник. Наблюдатель предполагается
неподвижным.

428. Найти построением ход луча после отражения в вогнутом и выпуклом сферических зеркалах (рис. 4.4 и рис. 4.5, где F - фокус, ОСУ - оптическая ось).

О-

F

Рис. 4.4

Рис. 4.5

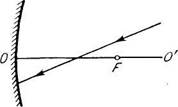
429. Найти построением положение зеркала и его фокуса для случаев, показанных на рис. 4.6 и 4.7, где Р и Р' -сопряженные точки.

0-

*р

о'

О

-О'

Рис. 4.6.

Рис. 4.7

430. Определить фокусное расстояние вогнутого зеркала,
если:

а) при расстоянии между предметом и изображением
/ = 15 см поперечное увеличение р = -2,0;

б) при одном положении предмета поперечное увеличение
Pj = -0,50, а при другом положении, смещенном относительно
первого на расстояние / = 5,0 см, поперечное увеличение
Р₂ = -0,25.

431. Точечный источник, сила света которого /₀ = 100 кд,
помещен на расстоянии s = 20,0 см от вершины вогнутого
зеркала с фокусным расстоянием /=25,0 см. Определить силу
света в отраженном пучке, если коэффициент отражения
зеркала р =0,80.

432. Вывести с помощью принципа Ферма формулу
преломления параксиальных лучей на сферической поверхности
радиуса R, разделяющей среды с показателями преломления л
и л'.

п

Рис. 4.8

Рис. 4.9

433. 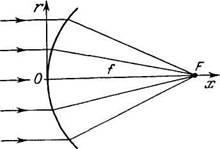Параллельный пу­
чок света падает из вакуу­
ма на поверхность, которая
ограничивает область с
показателем преломления
л (рис. 4.8). Найти форму
этой поверхности - урав­
нение х(г), при которой
пучок будет сфокусирован
в точке F на расстоянии
/ от вершины О. Пучок
какого максимального ра­
диуса сечения может быть
сфокусирован?

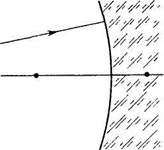
434. Луч света падает из воздуха на сферическую повер­
хность стекла (на рис. 4.9 точками отмечены положения
фокусов). Найти построением ход преломленного луча, считая
лучи параксиальными.

435. Точечный источник распо­
ложен на расстоянии 20 см от
передней поверхности стеклянной
симметричной двояковыпуклой
линзы. Толщина линзы 5,0 см,
радиус кривизны поверхностей 5,0
см. На каком расстоянии от задней
поверхности линзы образуется изо­
бражение источника?

436. Перед выпуклой поверх­
ностью стеклянной выпукло-плоской
линзы толщины ^ = 9,0см находит­
ся предмет. Его изображение обра­
зуется на плоской поверхности

линзы, которая служит экраном. Определить:

а) поперечное увеличение, если радиус кривизны выпуклой
поверхности линзы R = 2,5 см;

б) освещенность изображения, если яркость предмета
L = 7700 кд/м² и диаметр входного отверстия линзы D = 5,0 мм;
потерями света пренебречь.

437. Определить оптическую силу и фокусные расстояния
тонкой стеклянной линзы и жидкости с показателем преломле­
ния л_о = 1,7, если ее оптическая сила в воздухе Ф_о =-5,0 дптр.

438. Вычислить оптическую силу и фокусные расстояния
тонкой симметричной двояковыпуклой стеклянной линзы, с

одной стороны которой находится воздух, а с другой - вода, если оптическая сила этой линзы в воздухе Ф_о = +10 дптр.

439. Найти построением ход луча за собирающей и рассеивающей тонкими линзами (рис. 4.10 и 4.11, где ОО' -оптическая ось, F и F' — передний и задний фокусы).

о-

F

F'

-о¹

о-

F

-О'

Рис. 4.10

Рис. 4.11

4.40. Определить построением положение тонкой линзы и ее
фокусов, если известно положение оптической оси ОО' и
положение пары сопряженных точек Р и Р' (см. рис. 4.6 и 4.7).
Среды по обе стороны линз одинаковы.

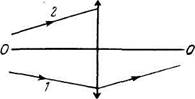
4.41. Найти построением ход луча 2 за собирающей и
рассеивающей тонкими линзами (рис. 4.12 и 4.13), если
известны положение линзы, ее оптической оси ОО' и ход луча
1. Среды по обе стороны линзы одинаковы.

О

-О'

Рис. 4.12

Рис. 4.13

4.42. Тонкая собирающая линза с фокусным расстоянием
/=25 см проецирует изображение предмета на экран, отстоящий
от линзы на 1 = 5,0 м. Экран придвинули к линзе не AZ = 18cm.
На сколько сантиметров следует переместить предмет, чтобы
опять получить четкое изображение его на экране?

4.43. Источник света находится на I = 90 см от экрана.
Тонкая собирающая линза, помещенная между источником
света и экраном, дает четкое изображение источника при двух
ее положениях. Найти фокусное расстояние линзы, если:

а) расстояние между обоими положениями А / = 30 см;

б) поперечные размеры изображения при одном положении
линзы в л =4,0 раза больше, чем при другом.

4.44. Между предметом и экраном поместили тонкую
собирающую линзу. Перемещением линзы нашли два положе­
ния, при которых на экране образуется четкое изображение
предмета. Найти поперечный размер предмета, если при одном
положении линзы размер изображения Л' = 2,0 мм, а при другом

А" = 4,5 мм.

4.45. Тонкая собирающая линза, у которой отношение ее

диаметра к фокусному расстоянию D:f= 1:3,5, дает изображение удаленного предмета на фотопленке. Яркость предмета L = 260 кд/м², потери света в линзе а =0,10. Найти освещенность изображения.

4.46. Как зависит от диаметра D тонкой собирающей линзы
яркость действительного изображения, если его рассматривать:

а) непосредственно;

б) на белом экране, рассеивающем по закону Ламберта?

4.47. Имеются две тонкие симметричные линзы: одна
собирающая с показателем преломления п_х = 1,70, другая
рассеивающая с и₂ = 1,51. Обе линзы имеют одинаковый радиус
кривизны поверхностей R = 10 см. Линзы сложили вплотную и
погрузили в воду. Каково фокусное расстояние этой системы в
воде?

4.48. Найти фокусное расстояние зеркала, представляющего
собой тонкую симметричную двояковыпуклую стеклянную линзу
с посеребренной одной поверхностью. Радиус кривизны

поверхностей линзы R = 40 см.

4.49. Система, состоящая из трех тонких линз (рис. 4.14),
находится в воздухе. Оптическая сила каждой линзы 10,0 дптр.
Определить:

а) положение точки схождения параллельного пучка, падающего слева, после прохождения через систему;

5,0 см

5,0см

о-

Рис. 4.14

б) расстояние от первой линзы до точки на оси слева от системы, при котором эта точка и ее изображение будут расположены симметрично относительно системы.

4.50. Галилеева труба 10-кратного увеличения при установке
на бесконечность имеет длину 45 см. Найти:

а) фокусные расстояния объектива и окуляра трубы;

б) на какое расстояние надо передвинуть окуляр трубы,
чтобы ясно видеть предметы на расстоянии 50 м.

4.51. Найти увеличение зрительной трубы кеплеровского
типа, установленной на бесконечность, если D - диаметр
оправы ее объектива, ad — диаметр изображения этой оправы,
образуемого окуляром трубы.

4.52. При прохождении светового потока через зрительную

трубу его интенсивность увеличивается в т] =4,0-10* раз. Найти угловой размер удаленного предмета, если при наблюдении в эту трубу угловой размер его изображения ф' = 2,0°.

4.53. Зрительную трубу кеплеровского типа с увеличением
Г = 15 погрузили в воду, которая заполнила и ее внутреннюю
часть. Чтобы система при тех же размерах стала опять
телескопической, объектив заменили другим. Каково стало после
этого увеличение трубы в воде? Показатель преломления стекла
окуляра п = 1,50.

4.54. При каком увеличении Г зрительной трубы с диамет­
ром объектива D = 6,0 см освещенность изображения объекта на
сетчатке глаза будет не меньше, чем в отсутствие трубы?
Диаметр зрачка глаза считать равным d₀ = 3,0 мм. Потерями
света в трубе пренебречь.

4.55. Оптические силы объектива и окуляра микроскопа
равны 100 и 20 дптр. Увеличение микроскопа равно 50. Каково
будет увеличение этого микроскопа, если расстояние между
объективом и окулярном увеличить на 2,0 см?

4.56. Микроскоп имеет числовую апертуру sin a =0,12, где
а - угол полураствора конуса лучей, падающих на оправу
объектива. Полагая диаметр зрачка глаза d₀ = 4,0 мм, определить
увеличение микроскопа, при котором диаметр светового пучка,
выходящего из микроскопа, равен диаметру зрачка глаза.

4.57. Исходя из условий предыдущей задачи, определить, при
каком увеличении микроскопа освещенность изображения на
сетчатке глаза не будет зависеть от увеличения. Считать, что
световой пучок, проходящий через систему "микроскоп - глаз",
ограничен оправой объектива.

4.58. Найти положение главных плоскостей, фокусов и
узловых точек двояковыпуклой тонкой симметричной стеклян-

ной линзы с радиусом кривизны поверхностей R - 7,50 см, если с одной стороны ее находится воздух, а с другой - вода.

4.59. Найти с помощью построения положение фокусов и главных плоскостей центрированных оптических систем, показанных на рис. 4.15:

0-

-О' 0-

d ф

------- *

-О'

N

■О'

ф,

ф₂

Рис. 4.15

а) телеобъектив — система из собирающей и рассеивающей
тонких линз (/j = \,5d, f₂ = -1,5*/);

б) система из двух собирающих тонких линз (./j = 1,5*/,
/а = 0,5rf);

в) толстая выпукло-вогнутая линза (d = 4cM, и = 1,5 Ф1 =
= +50дптр, Ф₂ = - 50 дптр).

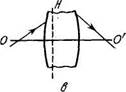
4.60. Оптическая система находится в воздухе. Пусть ОО' -ее оптическая ось, F и F - передний и задний фокусы, Н и Н' — передняя и задняя главные плоскости, Р и Р' — сопряженные точки. Найти построением:

а) положение F' и Н' (рис. 4.16а);

б) положение точки S', сопряженной с точкой S (рис. 4.166);

в) положение F,F' и Н' (рис. 4.16е, где показан ход луча
до и после прохождения системы).

О-

F

-0' О-

Н

-0'

.Р'

Рис. 4.16

4.61. Пусть F,F' - передний и задний фокусы оптической системы, Н и Я' - ее передняя и задняя главные точки. Найти

построением положение изображения S' точки S для следую­щих относительных расположений точек S,F,F,H,H': a) FSHH'F; б) HSFFH'; в) H'SF'FH; г) F'H'SHF.

4.62. Телеобъектив состоит из двух тонких линз — передней
собирающей и задней рассеивающей с оптическими силами
Ф, = +10 дптр иФ₂ = -Юдптр. Найти:

а) фокусное расстояние и положение главных плоскостей
этой системы, если расстояние между линзами d = 4,0 см;

б) расстояние d между линзами, при котором отношение
фокусного расстояния / системы к расстоянию I между
собирающей линзой и задним главным фокусом будет макси­
мальным. Чему равно это отношение?

4.63. Рассчитать положение главных плоскостей и фо­
кусов толстой выпукло-вогнутой стеклянной линзы, если ра­
диус кривизны выпуклой поверхности Л, = 10,0 см, вогнутой
/?2 = 5,0 см и толщина линзы d = 3,0 см.

4.64. Центрированная оптическая система состоит из двух
тонких линз с фокусными расстояниями /j и f₂, причем

расстояние между линзами равно d. Данную систему требуется заменить одной тонкой линзой, которая при любом положении объекта давала бы такое же поперечное увеличение, как и предыдущая система. Каким должно быть фокусное расстояние этой линзы и ее положение относительно системы из двух линз?

4.65. Система состоит из собирающей тонкой симметричной
стеклянной линзы с радиусом кривизны поверхностей Л = 38 см
и плоского зеркала, расположенного перпендикулярно оптичес­
кой оси линзы. Расстояние между линзой и зеркалом / = 12 см.
Какова будет оптическая сила этой системы, если пространство
между линзой и зеркалом заполнить водой?

4.66. При какой толщине выпукло-вогнутая толстая стеклян­
ная линза в воздухе будет:

а) телескопической, если радиус кривизны ее выпуклой
поверхности больше, чем радиус кривизны вогнутой поверхнос­
ти, на AR = 1,5 см;

б) иметь оптическую силу, равную -1,0 дптр, если радиусы
кривизны ее выпуклой и вогнутой поверхностей равны соответ­
ственно 10,0 и 7,5 см?

4.67. Найти положение главных плоскостей, фокусное
расстояние и знак оптической силы выпукло-вогнутой толстой
стеклянной линзы, у которой:

а) толщина равна d, а радиусы кривизны поверхностей одинаковы и равны R;

б) преломляющие поверхности концентрические с радиусами кривизны Л_х и /Jj (/^>/?j).

4.68. Телескопическая система образована из двух стеклян­
ных шаров, радиусы которых R_t = 5,0 см и R^ = 1,0 см. Каковы
расстояние между центрами этих шаров и увеличение системы,
если объективом является больший шар?

4.69. При распространении света в изотропной среде с
медленно изменяющимся от точки к точке показателем
преломления л радиус кривизны R луча определяется форму­
лой IfR = 3(lnn)/3iV, где производная берется по направлению
главной нормали к лучу. Получить эту формулу, имея в виду,
что в такой среде справедлив закон преломления n sin ft = const,
где Ь — угол между лучом и направлением gradn в данной
точке.

4.70. Найти радиус кривизны светового луча, распространяю­
щегося вдоль поверхности Земли, где градиент показателя

преломления воздуха dnjdN-Ъ 10~⁸ м"¹ (см. предыдущую задачу). При каком значении этого градиента луч света распространялся бы по окружности вокруг Земли?

42. Интерференция света

• Ширина интерференционной полосы:

Дх-X/q», (4.2 а)

где <р — угловое расстояние между источниками.

• Длина и радиус когерентности:

X, p_OT*A/4». (4.2 6)

где ф — угловой размер источника.

• При отражении света от оптически более плотной среды световой
вектор Б испытывает скачок фазы на я.

• Условие максимумов при интерференции света, отраженного от тонкой
пластинки толщины Ь

2fc^/n²-sin²f>=(* + l/2)A, (4.2 в)

где Ь — угол падения, к — целое число.

• Кольца Ньютона при отражении света от поверхностей воздушной
прослойки, образованной между стеклянной пластинкой и соприкасающейся с
ней выпуклой поверхностью линзы с радиусом кривизны R. Радиусы колец:

(4.2 г)

причем кольца светлые, если к= 1,3,5,..., и темные, если 4 = 2,4,6,... • Эффект Вавилова - Черенкова:

cosft =c/nv, (4.2 д)

где Ь - угол между направлением распространения излучения и скоростью V

частицы.

4.71. Показать, что при сложении двух гармонических
колебаний средняя по времени энергия результирующего
колебания равна сумме энергий каждого из них, если оба
колебания:

а) имеют одинаковое направление и некогерентны, причем
все значения их разности фаз равновероятны;

б) взаимно перпендикулярны, имеют одну и ту же частоту
и произвольную разность фаз.

4.72. Найти графически амплитуду колебания, которое
возникает в результате сложения следующих трех колебаний
одного направления:

л/3).

4.73. Некоторое колебание возникает в результате сложения N когерентных колебаний одного направления, имеющих следующий вид Ъ_к = acos[a>t + (к - 1) а], где к — номер колеба­ния (к = 1,2,... ,N), a — разность фаз между ifc-м и (£-1)-м колебаниями. Найти амплитуду результирующего колебания.

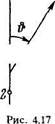4.74. Система (рис. 4.17) состоит из двух точеч­
ных когерентных излучателей 1 и 2, которые распо­
ложены в некоторой плоскости так, что их диполь-
ные моменты перпендикулярны этой плоскости.
'\ / Расстояние между излучателями d, длина волны

излучения X. Имея в виду, что колебания излучате­ля 2 отстают по фазе на а (а < п) от колебаний излучателя 1, найти:

а) углы Ь, в которых интенсивность излучения максимальна;

б) условия, при которых в направлении Ь = л интенсивность излучения будет максимальна, а в противоположном направле­нии - минимальна.

4.75. Найти примерный вид полярной диаграммы направлен­ности излучения в экваториальной плоскости системы, состоя­щей из двух одинаковых излучателей 1 и 2, дипольные моменты которых расположены параллельно друг другу на расстоянии d = к/2 и

а) совпадают по фазе;

б) противоположны по фазе.

4.76. То же, что в предыдущей задаче, но излучатели 1 и 2
находятся на расстоянии Я друг от друга.

4.77. То же, что в задаче 4.75, но излучатели / и 2 отстоят
друг от друга на расстояние d = XIА и колеблются со сдвигом

фаз я / 2.

4.78. Неподвижная излучающая система состоит из линейной
цепочки параллельных вибраторов, отстоящих друг от друга на
расстояние d, причем фаза колебаний вибраторов линейно
меняется вдоль цепочки. Найти зависимость от времени
разности фаз Д а между соседними вибраторами, при которой
главный максимум излучения системы будет совершать
круговой "обзор" местности с постоянной угловой скоростью «.

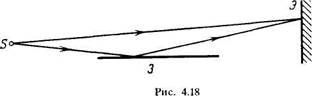
4.79. В опыте Ллойда (рис. 4.18) световая волна, исходящая
непосредственно из источника S (узкой щели), интерферирует
с волной, отраженной от зеркала 3. В результате на экране Э
образуется система интерференционных полос. Расстояние от
источника до экрана / = 100 см. При некотором положении
источника ширина интерференционной полосы на экране
Ад; = 0,25 мм, а после того, как источник отодвинули от
плоскости зеркала на ДЛ =0,60 мм, ширина полос уменьшилась
в г] = 1,5 раза. Найти длину волны света.

4.80. Две когерентные плоские световые волны, угол между

направлениями распространения которых <р<<1, падают почти нормально на экран. Амплитуды волн одинаковы. Показать, что

расстояние между соседними максимумами на экране Дд; = Я./<р, где Я — длина волны.

4.81. На рис. 4.19 показана интерференционная схема с
бизеркалами Френеля. Угол между зеркалами а = 12', расстоя­
ния от линии пересечения зеркал до узкой щели S и экрана
Э равны соответственно г = 10,0 см и Ъ = 130 см. Длина волны
света Я = 0,55 мкм. Определить:

а) ширину интерференционной полосы на экране и число возможных максимумов;

б) сдвиг картины на экране при смещении щели на
Ы = 1,0 мм по дуге радиуса г с центром в точке О;

в) при какой ширине щели А_маю интерференционные
полосы на экране будут наблюдаться еще достаточно отчетливо.

1-5"

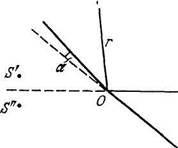
Рис. 4.19

4.82. Плоская световая волна падает на бизеркала Френеля,
угол между которыми а = 2,0'. Определить длину волны света,
если ширина интерференционной полосы на экране
Ах = 0,55 мм.

4.83. Линзу диаметром 5,0 см и с фокусным расстоянием
/=25,0 см разрезали по диаметру на две одинаковые половины,
причем удаленным оказался слой толщины а = 1,00 мм. После
этого обе половины сдвинули до соприкосновения и в фокаль­
ной плоскости полученной таким образом билинзы поместили
узкую щель, испускающую монохроматический свет с
Я = 0,64 мкм. За билинзой расположили экран на расстоянии
Ъ = 50 см от нее. Определить:

а) ширину интерференционной полосы на экране и число
N возможных максимумов;

б) ширину щели h_utKC, при которой полосы на экране будут
наблюдаться еще достаточно отчетливо.

4.84. Расстояния от бипризмы Френеля до узкой щели и
экрана равны соответственно а = 25 см и Ь = 100см. Бипризма
стеклянная с преломляющим углом 6 = 20'. Найти длину волны
света, если ширина интерференционной полосы на экране
Ад; = 0,55 мм.

4.85. Плоская световая волна с X = 0,70 мкм падает нормаль­
но на основание бипризмы, сделанной из стекла (л = 1,520) с
преломляющим углом 6 = 5,0°. За бипризмой (рис. 4.20)

находится плоскопараллельная стек- _ лянная пластинка, и пространство -, между ними заполнено бензолом -* (л'= 1,500). Найти ширину интерфе- ^ ренционной полосы на экране Э, _, расположенном за этой системой.

Рис. 4.20

4.86. Плоская монохроматическая
световая волна падает нормально на

диафрагму с двумя узкими щелями, отстоящими друг от друга на d = 2,5 мм. На экране, расположенном за диафрагмой на I = 100 см, образуется система интерференционных полос. На какое расстояние и в какую сторону сместятся эти полосы, если одну из щелей перекрыть стеклянной пластинкой толщины

А = 10 мкм?

4.87. На рис. 4.21 показана схема интерферометра для
измерения показателей преломления прозрачных веществ. Здесь
S - узкая щель, освещаемая монохроматическим светом
Я = 589 нм, 1 я 2 — две одинаковые трубки с воздухом, длина
каждой из которых / = 10,0 см, Д - диафрагма с двумя щелями.
Когда воздух в трубке 1 заменили аммиаком, то интерференци­
онная картина на экране Э сместилась вверх на N =11 полос.
Показатель преломления воздуха п = 1,000277. Определить
показатель преломления аммиака.

Д

Рис. 4.21

4.88. На поверхности стекла находится пленка воды. На нее
падает свет с Я = 0,68 мкм под углом Ь = 30° к нормали. Найти
скорость, с которой уменьшается толщина пленки (из-за
испарения), если интенсивность отраженного света меняется так,
что промежуток времени между последовательными максимума­
ми отражения Д* = 15мин.

4.89. На тонкую пленку (л = 1,33) падает параллельный пучок
белого света. Угол падения ft_x =52°. При какой толщине пленки
зеркально отраженный свет будет наиболее сильно окрашен в
желтый цвет (Х=0,60мкм)?

4.90. Найти минимальную толщину пленки с показателем
преломления 1,33, при которой свет с длиной волны 0,64 мкм
испытывает максимальное отражение, а свет с длиной волны
0,40 мкм не отражается совсем. Угол падения света равен 30°.

4.91. Для уменьшения потерь света из-за отражения от
поверхности стекла последнее покрывают тонким слоем

вещества с показателем преломления п'={п, где л - показа­тель преломления стекла. В этом случае амплитуды световых колебаний, отраженных от обеих поверхностей такого слоя, будут одинаковыми. При какой толщине этого слоя отражатель­ная способность стекла в направлении нормали будет равна нулю для света с длиной волны Я?

4.92. Рассеянный монохроматический свет с Я = 0,60 мкм
падает на тонкую пленку вещества с показателем преломления
п - 1,5. Определить толщину пленки, если угловое расстояние
между соседними максимумами, наблюдаемыми в отраженном
свете под углами с нормалью, близкими к Ь = 45°, равно
5 Ь = 3,0°.

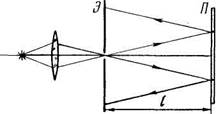
Рис. 4.22

4.93. Монохроматический свет проходит через отвер­стие в экране Э (рис. 4.22) и, отразившись от тонкой плос­копараллельной стеклянной пластинки 77, образует на экране систему интерферен­ционных полос равного на­клона. Толщина пластинки Ь, расстояние между ней и экраном /, радиусы i -го и

к-го темных колец r_t и г_к. Учитывая, что г._к«1, найти длину

волны света.

4.94. Плоская монохроматическая световая волна длины А
падает на поверхность стеклянного клина, угол между гранями
которого а < < 1. Плоскость падения перпендикулярна ребру
клина, угол падения t_t. Найти расстояние между соседними
максимумами интерференционных полос на экране, располо­
женном перпендикулярно отраженному свету.

4.95. Свет с X = 0,55 мкм от удаленного точечного источника
падает нормально на поверхность стеклянного клина. В
отраженном свете наблюдают систему интерференционных
полос, расстояние между соседними максимумами которых на
поверхности клина Ах = 0,21 мм. Найти:

а) угол между гранями клина;

б) степень монохроматичности света (Д Я/Я), если исчезно­вение интерференционных полос наблюдается на расстоянии

/ «1,5 см от вершины клина.

Дата добавления: 2015-08-02