Ffl, ffU

F = i-±-±. (1.4a)

г²

• Квадраты периодов обращения планет вокруг Солнца относятся как
кубы больших полуосей их орбит (Кеплер):

Г² <м а³. (1.46)

• Потенциал гравитационного поля точечной массы:

<р =-ути/г. (1-4в)

• Первая и вторая космические скорости:

, 1/2=1/,,/2. (1.4г)

1237. Некоторая планета массы А/ движется по окружности вокруг Солнца со скоростью v = 34,9 км/с (относительно гелиоцентрической системы отсчета). Найти период обращения этой планеты вокруг Солнца.

1238. Период обращения Юпитера вокруг Солнца в 12 раз
больше соответствующего периода для Земли. Считая орбиты
планет круговыми, найти:

а) во сколько раз расстояние от Юпитера до Солнца
превышает расстояние от Земли до Солнца;

б) скорость и ускорение Юпитера в гелиоцентрической
системе отсчета.

1239. Планета массы М движется вокруг Солнца по эллипсу
так, что минимальное расстояние между ней и Солнцем равно
r_v а максимальное г₂, Найти с помощью (1.46) период
обращения ее вокруг Солнца.

1240. Два спутника движутся вокруг Земли по касающимся
траекториям. Один спутник движется по окружности радиуса г,
другой — по эллипсу с периодом обращения, в ц раз боль­
шим, чем у первого спутника. Найти с помощью (1.46)
максимальное расстояние между вторым спутником и центром
Земли.

1.241. Небольшое тело начинает падать на Солнце с расстояния, равного радиусу земной орбиты. Найти с помощью (1.46) продолжительность падения.

1242. Спутник Луны, двигавшийся по круговой орбите
радиуса г, после кратковременного торможения стал двигаться
по эллиптической орбите, касающейся поверхности Луны,
Найти с помощью (1.46) время падения спутника на Луну.

1243. Представим себе, что мы создали модель Солнечной
системы, к Ti раз меньшую натуральной величины, но из
материалов той же самой средней плотности, что у Солнца и
планет. Как изменятся при этом периоды обращения моделей
планет по своим орбитам?

1.244. Двойная звезда — это система из двух звезд, движу­
щихся вокруг ее центра масс. Известны расстояние / между
компонентами двойной звезды и период Т ее вращения.
Считая, что / не меняется, найти массу системы.

1.245. Планета массы m движется по эллипсу вокруг Солнца
так, что наименьшее и наибольшее расстояния ее от Солнца
равны соответственно г_х и г₂. Найти момент импульса М этой
планеты относительно центра Солнца.

1246. Доказать с помощью законов сохранения, что полная
механическая энергия Е планеты массы т, движущейся вокруг
Солнца по эллипсу, зависит только от его большой полуоси а.
Найти зависимость Е(а).

1247. Планета А движется по эллиптической орбите вокруг
Солнца. В момент, когда она находилась на расстоянии г₀ от

Солнца, ее скорость равнялась v₀ и угол между радиусом-вектором 1$ и вектором скорости v₀ составлял а. Найти наибольшее и наименьшее расстояния, на которые удаляется от Солнца эта планета при своем движении.

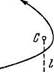
1248. Космическое тело А дви­
жется к Солнцу С, имея вдали от
него скорость v₀ и прицельный
параметр / — плечо вектора v₀
относительно центра Солнца
(рис. 1.48). Найти наименьшее рас- д
стояние, на которое это тело при­
близится к Солнцу. "

1249. Частица массы т нахо- Рис. 1.48
дится вне однородного шара массы

М на расстоянии г от его центра. Найти:

а) потенциальную энергию гравитационного взаимодействия
частицы и шара;

б) силу, с которой шар действует на частицу.

1250. Доказать, что сила тяготения, действующая на частицу
Л внутри однородного сферического слоя вещества, равна нулю.

Имеется однородный шар массы М и радиуса R. Найти напряженность G и потенциал ср гравитационного поля этого шара как функции расстояния г от его центра (при r<R и r>R). Изобразить примерные графики зависимостей G(r) и q>(r).

1.252. Внутри однородного шара плотности р имеется
сферическая полость, центр которой находится на расстоянии
1 от центра шара. Найти напряженность G поля тяготения
внутри полости.

1253. Однородный шар имеет массу М и радиус R. Найти
давление р внутри шара, обусловленное гравитационным
сжатием, как функцию расстояния г от его центра. Оценить р
в центре Земли, считая, что Земля является однородным
шаром.

1254. Найти собственную потенциальную энергию гравитаци­
онного взаимодействия вещества, образующего:

а) тонкий однородный сферический слой массы т и
радиуса R;

б) однородный шар массы т и радиуса R (воспользоваться
ответом к задаче 1.251).

1255. Вычислить отношение следующих ускорений: ускоре­
ния а_х, вызываемого силой тяготения на поверхности Земли;

ускорения a_z, обусловленного центробежной силой инерции на экваторе Земли; ускорения а_г, сообщаемого телами на Земле Солнцем.

1256. На какой высоте над полюсом Земли ускорение
свободного падения убывает на т\ = 1,0 %? в п = 2,0 раза?

1257. Телу сообщили на полюсе Земли скорость v₀,
направленную вертикально вверх. Зная радиус Земли и
ускорение свободного падения на ее поверхности, найти высоту,
на которую поднимается тело.

1.258. Найти период обращения спутника, движущегося вокруг некоторой планеты вблизи ее поверхности, если средняя

плотность планеты р = 3,3 г/см³.

1259. Спутник вывели на круговую орбиту со скоростью v
над полюсом Земли. Найти расстояние от спутника до
поверхности Земли.

1260. Спутник Земли массы m движется по круговой
орбите, радиус которой вдвое больше радиуса Земли. Какой
дополнительный импульс и в каком направлении следует
кратковременно сообщить спутнику, чтобы плоскость его
орбиты повернулась на угол а без изменения радиуса орбиты?

1261. Вычислить радиус круговой орбиты стационарного
спутника Земли, который остается неподвижным относительно
ее поверхности. Какова его скорость в инерциальной системе
отсчета, связанной в данный момент с центром Земли?

1262. Система, которая состоит из двух одинаковых
спутников, соединенных тонким тросом длины / = 150 м,
движется по круговой орбите вокруг Земли. Масса каждого
спутника m = 1000 кг, масса троса пренебрежимо мала, расстоя­
ние от центра Земли до этой системы составляет х\ = 1,2
радиуса Земли. Найти силу натяжения троса в момент, когда
трос направлен по радиусу Земли.

1263. Найти массу Земли, если спутник, движущийся в ее
экваториальной плоскости с запада на восток по круговой

орбите радиуса R = 2,00 • 10⁴ км, появляется над некоторым пунктом на экваторе через каждые т = 11,6 ч.

1264. Спутник движется в экваториальной плоскости Земли

с востока на запад по круговой орбите радиуса Л = 1,00 -10* км. Найти относительно поверхности Земли: а) скорость спутника; б) его ускорение.

1265. Какую скорость необходимо сообщить телу в горизон­
тальном направлении вблизи поверхности Земли у ее полюса,
чтобы вывести его на эллиптическую орбиту с большой
полуосью а?

1266. Искусственный спутник Луны движется по круговой
орбите, радиус которой в ц раз больше радиуса Луны. Считая,
что небольшая сила сопротивления, испытываемая спутником
со стороны космической пыли, зависит от его скорости как

F = а и², где а — постоянная, найти время движения спутника до падения на поверхность Луны.

1267. Вычислить первую и вторую космические скорости для
запусков с Луны. Сравнить с соответствующими скоростями
для Земли.

1268. Космический корабль подлетает к Луне по параболи­
ческой траектории, почти касающейся ее поверхности. В
момент максимального сближения с Луной на короткое время
был включен тормозной двигатель, и корабль перешел на
круговую орбиту. Найти приращение модуля скорости корабля
при торможении.

1269. Космический корабль вывели на круговую орбиту
вблизи поверхности Земли. Какую дополнительную скорость в
направлении его движения необходимо кратковременно сооб­
щить кораблю, чтобы он смог преодолеть земное тяготение?

1270. Космический корабль движется вокруг Земли по
круговой орбите, радиус которой в ц = 2,5 раза больше ра­
диуса Земли. Какую дополнительную скорость надо кратко­
временно сообщить кораблю в направлении от центра Земли
по ее радиусу, чтобы он смог покинуть поле тяготения
Земли?

1271. Найти приближенно третью космическую скорость
v₃ — наименьшую скорость, которую необходимо сообщить

телу относительно поверхности Земли, чтобы оно могло покинуть Солнечную систему. Вращением Земли вокруг ее оси пренебречь.

Дата добавления: 2015-08-02