
Читайте также:
|
• Магнитное поле точечного заряда q, движущегося с нерелятивистской
скоростью v:
B = (iK)/4«)g[vr]/r3. (2.5а)
• Закон Био —Савара:
(2,б)
Циркуляция вектора В (в вакууме) и теорема Гаусса:
JBdt = v0I, fbdS = 0. (2.5в)
Сила Лоренца:
F = «E + «|yB]. (2.5г)
Сила Ампера:
dV-l[dl,B]. (2.5д)
• Сила и момент сил, действующие на магнитный диполь pm = /5n:
Г=ртдВ/дп, N = [pBB], (2.5e)
где ЭВ/Эп - производная вектора В по направлению диполя.
• Элементарная работа амперовых сил при перемещении контура с током:
6А=1ЫФ. (2.5ж)
• Циркуляция намагниченности I:
jjdt = l', (2.5з)
где /' — ток намагничения (молекулярный ток).
• Вектор Н и его циркуляция:
H-B/|»o-J, jndt = l, (2.5и)
где / - алгебраическая сумма макроскопических токов.
• Условия на границе раздела двух магнетиков:
Ви=В2»> HU = HU. (2.5к)
• Для магнетиков, у которых J = xH:
В=цц„Н, ц=1 + Х- (2.5л)
2225. Точечный заряд движется со скоростью v = 900 м/с.
В некоторый момент в точке Р напряженность поля этого
заряда £ = 600 В/м, а между векторами Е и v угол а = 30°.
Найти индукцию В магнитного поля данного заряда в точке Р
в этот момент.
2226. По круговому витку радиуса R = 100 мм из тонкого про
вода циркулирует ток 7=1,00 А. Найти магнитную индукцию:
а) в центре витка;
б) на оси витка на расстоянии х = 100 мм от его центра.
2227. Кольцо радиуса R - 50 мм из тонкого провода согнули
по диаметру под прямым углом. Найти магнитную индукцию
в центре кривизны полуколец при токе / = 2,25 А.

|
| Рис. 2.60 |
2228. Ток / течет по плоскому кон
туру, показанному на рис. 2.60, где г =
= го(1 + «р). Найти магнитную индукцию В
в точке О.
2229. Ток / течет по тонкому провод
нику, который имеет вид правильного
я-угольника, вписанного в окружность
радиуса R. Найти магнитную индукцию в
центре данного контура. Исследовать
случай п - оо.

|
2230. Найти машитную индукцию в
центре контура, имеющего вид прямоу
гольника, если его диагональ d = 16 см,
угол между диагоналями <р = 30е и ток
7 = 5,0 А.
| Рис. 2.61 |
2.231. Ток / = 5,0 А течет по тонкому замкнутому проводнику (рис. 2.61). Радиус изогнутой части R = 120 мм, угол 2ф = 90". Найти магнитную индукцию в точке О.
2232. Найти индукцию магнитного поля в точке О контура с током /, который показан:
а) на рис. 2.62; радиусы а и Ъ, а также угол ср известны;
б) на рис. 2.63; радиус а и сторона b известны.

|

|
Рис. 2.62
Рис. 2.63
2.233. Ток / течет вдоль длинной тонкостенной трубы радиуса R, имеющей по всей длине продольную прорезь ширины h. Найти индукцию магнитного поля внутри трубы, если h «R.

|
2234. Ток /=11,0 А течет по длинному
прямому проводнику, сечение которого имеет
форму тонкого полукольца радиуса R = 5,0 см
(рис. 2.64). Найти магнитную индукцию на
оси О.
| Рис. 2.64 |
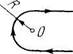
2235. Определить магнитную индукцию в
точке О, если проводник с током / имеет
вид, показанный:
а) на рис. 2.65; б) на рис. 2.66; в) на рис. 2.67.
|

|

|
Рис. 2.66
Рис. 2.67
Радиус изогнутой части проводника равен R, прямолинейные участки проводника очень длинные.
|
2236. Длинный проводник с током
/ изогнут, как показано на рис. 2.68.
Расстояние а известно. Найти магнит
ную индукцию:
а) в точке 1; б) в точке 2.
| Рис. 2.68 |
| Рис. 2.69 |
2237. Длинный проводник с током
1 = 5,0 А изогнут под прямым углом.
Найти магнитную индукцию в точке,
которая отстоит от плоскости проводни
ка на /= 35 см и находится на перпен
дикуляре, проходящем через точку
изгиба.
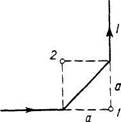
2238. Длинный провод с током /
изогнут под прямым углом. Найти маг
нитную индукцию в точках 1 и 2,
находящихся на биссектрисе этого угла
на расстоянии / от точки изгиба
(рис. 2.69).
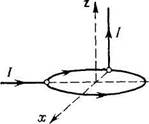
2239. Найти магнитную индукцию в
точке О, если проводник с током
7=8,0 А имеет вид, показанный:
а) на рис. 2.70; б) на рис. 2.71.
Радиус изогнутой части проводника R = 100 мм, прямолинейные участки проводника очень длинные.

|

|
| У |
Рис. 2.70
Рис. 2.71
|
2.240. Ток / течет по длинным прямым проводникам, которые подключены к двум точкам однородного проводника, имеющего вид кольца радиуса R (рис. 2.72). Найти магнитную
индукцию в точке О.
| Рис. 2.72 |
2241. Определить индукцию
магнитного поля тока, равномер
но распределенного:
а) по плоскости с линейной
плотностью i;
б) по двум параллельным плоскостям с линейными плот
ностями i и - i.
2242. Однородный ток плотности j течет внутри неограни
ченной пластины толщины Id параллельно ее поверхности.
Пренебрегая влиянием вещества пластины, найти индукцию
магнитного поля этого тока как функ
цию расстояния х от средней плоскос
ти пластины.
| А |
| Рис. 2.73 |
2.243.  Постоянный ток / течет по
Постоянный ток / течет по
длинному проводу и далее растекается
радиально-симметрично по проводя
щей плоскости, перпендикулярной
проводу. Найти индукцию магнитного
поля во всех точках пространства.
2.244. Ток / течет по длинному
проводу и затем растекается равно
мерно по всем направлениям в одно
родной проводящей среде (рис. 2.73).
Пренебрегая влиянием вещества сре-
ды, найти индукцию магнитного поля в точке А, отстоящей от точки О на расстояние г под углом Ь.
2.245. Имеется круговой виток с током /. Найти интеграл
\Bxdx вдоль оси витка в пределах от -«> до +оо.
2246. По прямому проводу, радиус сечения которого R,
течет постоянный ток плотности j. Пренебрегая влиянием
вещества провода, найти индукцию магнитного поля этого тока
в точке, положение которой относительно оси провода опреде
ляется радиусом-вектором г.
2247. Внутри длинного прямого провода круглого сечения
имеется длинная круглая цилиндрическая полость, ось которой
параллельна оси провода и смещена относительно последней
на расстояние 1. По проводу течет постоянный ток плотности
j. Пренебрегая влиянием вещества провода, найти индукцию
магнитного поля внутри полости.
2248. Найти плотность тока как функцию расстояния г от
оси аксиально-симметричного параллельного потока электронов,
если индукция магнитного поля внутри потока В - Ьгл, где Ь и а — положительные постоянные.
2249. Однослойный соленоид имеет длину /, радиус сечения
R и число витков на единицу длины и. Найти индукцию
магнитного поля в центре соленоида, если ток в обмотке
равен /.
2250. Длинный соленоид имеет радиус сечения R и и
витков на единицу длины. По нему течет постоянный ток /.
Найти индукцию магнитного поля на оси как функцию коорди
наты х, отсчитываемой вдоль оси соленоида от его торца.
Изобразить примерный график зависимости индукции В от
отношения xjR.
2251. Обмоткой длинного соленоида с радиусом сечения
R = 2,5 см служит тонкая лента-проводник ширины h = 5,0 см,
намотанная в один слой практически вплотную. По ленте течет
ток / = 5,0 А. Найти индукцию магнитного поля внутри и вне
соленоида как функцию расстояния г от его оси.
2252. На деревянный тороид малого поперечного сечения
намотано равномерно # = 2,5-10* витков провода, по которому течет ток /. Найти отношение х\ магнитной индукции внутри тороида к индукции в его центре.
2253. Ток / = 10 А течет по длинному прямому проводнику
круглого сечения. Пренебрегая влиянием вещества проводника,
найти магнитный поток через одну из половин осевого сечения
проводника в расчете на единицу его длины.

|
| Рис. 2.74 |

|
| Рис. 2.75 |

|
2254. Имеется длинной соленоид с током /. Площадь его
поперечного сечения S, число витков на единицу длины и.
Найти магнитный поток через торец соленоида.
2255. На рис. 2.74 показан
кольцевой соленоид прямоуголь
ного сечения. Найти магнитный
поток через это сечения, если
ток в обмотке / = 1,7 А, полное
число витков N = 1000, отно
шение внешнего диаметра к
внутреннему х\ = 1,6 и толщина
А =5,0 см.
2256. Найти магнитный мо
мент тонкого кругового витка с
током, если радиус витка R =
= 100 мм и индукция магнит
ного поля в его центре В =
= 6,0 мкТл.
2257. Вычислить магнитный
момент тонкого проводника с
током / = 0,8 А, плотно навитого
на половину тора (рис. 2.75).
Диаметр сечения тора d = 5,0 см, число витков JV = 500.
2258. Тонкий провод (с изо
ляцией) образует плоскую спи
раль из N = 100 плотно располо
женных витков, по которым
течет ток / = 8мА. Радиусы
внутреннего и внешнего витков
(рис. 2.76) равны а = 50 мм, Ъ =
= 100 мм. Найти:
| Рис. 2.76 |
а) индукцию В магнитного
поля в центре спирали;
б) магнитный момент спира
ли при данном токе.
2259. Равномерно заряженное зарядом q тонкое непроводя
щее кольцо массы т вращается с большой угловой скоростью
вокруг своей оси во внешнем однородном магнитном поле с
индукцией В. Найти угловую скорость прецессии ы', если ось
кольца составляет некоторый угол с вектором В.
2260. Непроводящий тонкий диск радиуса R, равномерно
заряженный с одной стороны с поверхностной плотностью а,
вращается вокруг своей оси с угловой скоростью со. Найти:
а) индукцию магнитного поля в центре диска;
б) магнитный момент диска.
2261. Непроводящая сфера радиуса R = 50 мм, заряженная
равномерно с поверхностной плотностью а = 10,0 мкКл/м2,
вращается с угловой скоростью со = 70 рад/с вокруг оси, проходя
щей через ее центр. Найти магнитную индукцию в центре
сферы.
2262. Заряд q равномерно распределен по объему однород
ного шара массы т и радиуса R, который вращается вокруг
оси, проходящей через его центр, с угловой скоростью со.
Найти соответствующий магнитный момент и его отношение
к механическому моменту.
2263. Длинный диэлектрический цилиндр радиуса R
статически поляризован так, что во всех его точках поляризо-
ванность Pwr, где г — расстояние от оси. Цилиндр привели во вращение вокруг его оси с угловой скоростью со. Найти индукцию магнитного поля на оси цилиндра.
2.264. Два протона движутся параллельно друг другу с одинаковой скоростью v = 300 км/с. Найти отношение сил магнитного и электрического взаимодействия данных протонов.
 2265. Найти модуль и направление силы,
2265. Найти модуль и направление силы,
действующей на единицу длины тонкого
п \ проводника с током 1 = 8,0 А в точке О, —т. <—1 если проводник изогнут, как показано:
а) на рис. 2.77, и радиус закругления
R = 10 см;
| п |
б) на рис. 2.78, и расстояние между длин
ными параллельными друг другу участками
проводника / = 20 см.
2266. Два длинных прямых взаимно пер-
Рис. 2.78 пендикулярных провода отстоят друг от
друга на расстояние а. В каждом проводе течет ток /. Найти максимальное значение силы Ампера на единицу длины провода в этой системе.
2267. Катушку с током / = 10 мА поместили в однородное магнитное поле так, что ее ось совпала с направлением поля. Обмотка катушки однослойная из медного провода диаметром d = 0,10 мм, радиус витков Я = 30 мм. При каком значении индукции внешнего поля обмотка катушки может быть разорвана?
2.268. Соленоид с током / и числом витков и на единицу длины находится в аксиально-симметричном магнитном поле, ось симметрии которого совпадает с осью соленоида. Найти модуль силы, действующей на соленоид, если магнитные потоки, входящий и выходящей через торцы соленоида, равны Ф1 и Ф2.
2269. Имеется длинный соленоид, у которого радиус
R = 30 мм и число витков на единицу длины п =20 см"1. С какой магнитной силой одна половина этого соленоида действует на другую половину, если ток в соленоиде / = 1,3 А?

|
2270. Медный провод сечением S =
= 2,5 мм2, согнутый в виде трех сторон квадрата, может поворачиваться вокруг
горизонтальной оси ОО' (рис. 2.79). Провод находится в однородном вертикально направленном магнитном поле. Найти индукцию поля, если при пропускании по данному проводу тока / = 16 А угол отклонения 0 = 20°.
| Рис. 2.79 |
2271. Замкнутый контур с током /
находится в поле длинного прямого провод
ника с током Jo. Плоскость контура перпен
дикулярна прямому проводнику. Найти
момент сил Ампера, действующих на замкнутый контур, если он имеет вид:
а) как на рис. 2.80; б) как на рис. 2.81.
Необходимые размеры системы указаны на рисунке.

|

|
Рис. 2.80
Рис. 2.81
2.272. Укрепленную на конце коромысла весов небольшую катушку К с числом витков N = 200 поместили в зазор между полюсами магнита (рис. 2.82). Площадь сечения катушки
| у////, S = 1,0 см2, длина плеча
J\_______ ОЛ коромысла / = 30 см. В \ отсутствие тока через ка- _________ \ тушку весы уравновешены.
После того как через ка-
К (fflH |
 v/ // //X, х весия пришлось изменить
v/ // //X, х весия пришлось изменить
груз на чаше весов на
Д/й = 60мг. Найти индук-
Рис. 2.82 цИЮ магнитного поля в
месте нахождения катушки.
2273. Квадратная рамка с током / = 0,90 А расположена в
одной плоскости с длинным прямым проводником, по которо
му течет ток /0 = 5,0 А. Сторона рамки а = 8,0 см. Проходящая
через середины противоположных сторон ось рамки параллель
на проводу и отстоит от него на расстояние, которое в
т| = 1,5 раза больше стороны рамки. Найти:
а) амперову силу, действующую на рамку;
б) механическую работу, которую нужно совершить при
медленном повороте рамки вокруг ее оси на 180°.
2274. Два параллельных длинных провода с током / = 6,0 А
в каждом (токи направлены в одну сторону) удалили друг от
друга так, что расстояние между ними стало в ц = 2,0 раза
больше первоначального. Какую работу на единицу длины
проводов совершили при этом силы Ампера?
2275. Два длинных параллельных провода с пренебрежимо
малым сопротивлением с одного конца замкнуты на сопротив
ление R, а с другого конца подключены к источнику постоян
ного напряжения. Расстояние между осями проводов в
т| = 20 раз больше радиуса сечения каждого провода. При каком
R сила взаимодействия между проводами обратится в нуль?
2276. Постоянный ток / = 14 А течет по длинному прямому
проводнику, сечение которого имеет форму тонкого полукольца
радиуса Я = 5,0 см. Такой же ток течет в противоположном
направлении по тонкому проводнику, расположенному на "оси"
первого проводника (точка О на рис. 2.64). Найти силу магнит
ного взаимодействия данных проводников на единицу их длины.
2.277. Внутри длинного цилиндрического сосуда радиуса а параллельно его оси расположен проводящий стержень радиуса Ъ с тонкой изоляцией. Расстояние между осями стержня и сосуда равно /. Сосуд заполнили электролитом и пустили вдоль оси ток /, возвращающийся обратно по стержню. Найти
модуль и направление магнитной силы, действующей на единицу длины стержня.
| h |

|
| Рис. 2.83 |
2278. По двум длинным тонким параллельным проводникам, вид которых показан на рис. 2.83, текут постоянные токи /t и /2., Расстояние между проводниками а, ширина ; правого проводника Ъ. Имея в виду, что оба проводника лежат в одной плоскости, найти силу магнитного взаимодействия между ними в расчете на единицу их длины.
2219. Система состоит из двух параллельных друг другу плоскостей с токами, которые создают между плоскостями однородное магнитное поле с индукцией В. Вне этой области магнитное поле отсутствует. Найти магнитную силу, действующую на единицу поверхности каждой плоскости.
2280. Проводящую плоскость с током поместили во внешнее однородное магнитное поле. В результате индукция магнитного поля с одной стороны плоскости оказалась Вх, ас другой стороны В2. Найти магнитную силу, действующую на единицу поверхности плоскости в случаях, показанных на рис. 2.84. Выяснить, куда направлен ток в плоскости в каждом случае.
 |

|
| В, |
в,
6
Рис.2.84

|
2281, В электромагнитном насосе для перекачки расплавленного металла участок трубы с металлом находится в однородном магнитном поле с индукцией В (рис. 2.85). Через этот участок трубы в перпендикулярном вектору В и оси трубы направлении пропускают равномерно распределенный ток /. Найти избыточ-
Рис. 2.85
ное давление, создаваемое насосом при В = 0,10Тл, 7=100 А и а = 2,0 см.
2282. Вдоль длинного тонкостенного круглого цилиндра
радиуса R = 5,0 см течет ток 7 = 50 А. Какое давление испытывают стенки цилиндра?
2283. Какое давление испытывает боковая поверхность
длинного прямого соленоида, содержащего п =20 виток/см, когда
по нему течет ток / = 20 А?
2284. Ток / течет по длинному однослойному соленоиду,
радиус сечения которого Л =5,5 см. Число витков на единицу
длины соленоида и = 15 см"1. Найти предельную силу тока, при которой может наступить разрыв обмотки, если предельная нагрузка на разрыв проволоки обмотки Fnp=100 H.
2285. Плоский конденсатор, площадь каждой пластины
которого S и расстояние между ними d, поместили в поток
проводящей жидкости с удельным сопротивлением р. Жидкость
движется со скоростью v параллельно пластинам. Система
находится в однородном магнитном поле с индукцией В,
причем вектор В параллелен пластинам и перпендикулярен
направлению потока. Пластины конденсатора замкнули на
внешнее сопротивление R. Какая мощность Р выделяется на
этом сопротивлении? При каком R мощность Р максимальна?
Чему равна Рыт?
2286. Вдоль медного прямого проводника радиуса R = 5,0 мм
течет ток / = 50 А. Найти разность потенциалов между осью
проводника и его поверхностью. Концентрация электронов
проводимости у меди и = 0,9-10м см"3.
2287. При измерении эффекта Холла в натриевом проводни
ке напряженность поперечного поля оказалась Е = 5,0 мкВ/см
при плотности тока j = 200 А/см2 и индукции магнитного поля
В = 1,00 Тл. Найти концентрацию электронов проводимости и ее
отношение к концентрации атомов в данном проводнике.
2288. Найти подвижность электронов проводимости в
медном проводнике, если при измерении эффекта Холла в
магнитном поле с индукцией В = 100 мТл напряженность
поперечного электрического поля у данного проводника
оказалась в л = 3,1 • 103 раз меньше напряженности продольного электрического поля.
2289. Небольшой виток с током находится на расстоянии г
от длинного прямого проводника с током /. Магнитный
момент витка равен рт. Найти модуль и направление силы,
действующей на виток, если вектор р:
а) параллелен прямому проводнику;
б) направлен по радиусу-вектору г;
в) совпадает по направлению с магнитным полем тока /
и месте расположения витка.
2290. Небольшая катушка с током, имеющая магнитный
момент рт, находится на оси кругового витка радиуса R, по
которому течет ток /. Найти модуль силы, действующей на
катушку, если ее расстояние от центра витка равно х, а вектор
Рщ совпадает по направлению с осью витка.
2291. Найти силу взаимодействия двух катушек с магнитны
ми моментами />lm = 4,0 мАм2 и р2т= 6,0 мА ■ и2, если их оси
лежат на одной прямой и расстояние между катушками
/ = 20 см значительно превышает их линейные размеры.
2292. Постоянный магнит имеет форму достаточно тонкого
диска, намагниченного вдоль его оси. Радиус диска R = 1,0 см.
Оценить значение молекулярного тока /', текущего по ободу
диска, если индукция магнитного поля на оси диска в точке,
отстоящей на х = 10 см от центра, составляет В = 30мкТл.
2293. Индукция магнитного поля в вакууме вблизи плоской
поверхности однородного изотропного магнетика равна В,
причем вектор В составляет угол а с нормалью к поверхности.
Магнитная проницаемость магнетика ц. Найти индукцию В'
магнитного поля в магнетике

|
вблизи поверхности.
| Рис. 2.86 |
2294. Индукция магнит
ного поля в вакууме вбли
зи плоской поверхности маг
нетика равна В, и вектор
В составляет угол Ь с нор
малью п к поверхности
(рис. 2.86). Магнитная про
ницаемость магнетика \i.
Найти:
| R, центр которой лежит на |
а) поток вектора Н через
поверхность сферы S радиуса
поверхности магнетика;
б) циркуляцию вектора В по квадратному контуру Г со
стороной /, расположенному, как показано на рисунке.
2.295. Постоянный ток / течет вдоль длинного цилиндрического провода круглого сечения. Провод сделан из парамагнетика с восприимчивостью %. Найти:
а) поверхностный молекулярный ток /'ПОЕ;
б) объемный молекулярный ток Г^.
Как эти точки направлены друг относительно друга?
2296. Длинный соленоид заполнен неоднородным парамагне
тиком, восприимчивость которого зависит только от расстояния
г до оси соленоида как % = аг2, где а — постоянная. На оси соленоида индукция магнитного поля равна Во. Найти зависимость от г:
а) намагниченности магнетика У (г);
б) плотности молекулярного тока j'(r) в магнетике.
2297. Длинный соленоид с током наполовину заполнен
парамагнетиком (рис. 2.87). Изобразить примерные графики

|
индукции В, напряженности Н и намагниченности J на оси соленоида в зависимости ОТ X.
Рис' г87 2298. Прямой бесконеч-
но длинный проводник с
током / лежит в плоскости раздела двух непроводящих сред с магнитными проницаемостями \ix и ^2. Найти индукцию В магнитного поля во всем пространстве в зависимости от расстояния г до провода. Известно, что линии В являются окружностями с центром на оси проводника.
2299. Круговой контур с током лежит на плоской поверхности магнетика с проницаемостью ц. Найти индукцию В магнитного поля в некоторой точке на оси контура, если в отсутствие магнетика индукция в этой точке равна Во. Обобщить полученный результат на все поле.
2.300. Известно, что внутри шара, намагниченного однородно и статически, напряженность магнитного поля H' = -J/3, где J - намагниченность. Имея в виду это соотношение, найти индукцию магнитного поля в шаре из однородного магнетика с проницаемостью ц, помещенного во внешнее однородное магнитное поле с индукцией Во (при этом шар намагнитится однородно).
2301. Имеется бесконечная пластина из однородного ферромагнетика с намагниченностью J. Найти векторы В и Н внутри и вне пластины, если вектор J направлен относительно поверхности пластины:
а) перпендикулярно; б) параллельно.
| Jt |
| Н |
| Рис. 2.88 |
2302.  На постоянный магнит, имеющий форму тонкого
На постоянный магнит, имеющий форму тонкого
цилиндра длины / = 15 см, намотали равномерно N = 300 витков
провода. При пропускании по нему тока / = 3,0 А поле вне
магнита исчезло. Найти коэрцитивную силу Но материала
магнита.
2303. Постоянный магнит имеет вид кольца с узким зазором
между полюсами. Средний диаметр кольца d = 20cM. Ширина
зазора Ь=2,0 мм, индукция магнитного поля в чазоре В =
= 40мТл. Пренебрегая рассеянием магнитного поля на краях
зазора, найти модуль напряженности магнитного поля внутри
магнита,
2304. Постоянный магнит имеет вид
кольца с узким поперечным зазором
ширины Ъ = 2,5 мм. Средний радиус
кольца а =5,0 см. Остаточная намагничен
ность материала магнита Jr= 1000 кА/м,
его коэрцитивная сила #с = 25 кА/м.
Считая, что зависимость / (Я) на участке
от Нс до нуля (рис. 2.88) является линей
ной и рассеяния магнитного поля на
краях зазора нет, найти индукцию маг
нитного поля в зазоре.
2305. На железном сердечнике в виде
тора со средним радиусом R = 250 мм
имеется обмотка с числом витков N =
= 1000. В сердечнике сделана поперечная прорезь ширины Ъ = 1,00 мм. При токе / = 0,85 А через обмотку индукция магнитного поля в зазоре 5 = 0,75 Тл. Пренебрегая рассеянием магнитного поля на краях зазора, найти магнитную проницаемость железа в этих условиях.
2306. На рис. 2.89 показана основная кривая намагничива
ния технически чистого железа. Построить с помощью этого
графика кривую зависимости магнитной проницаемости \х от
напряженности Н магнитного поля. При каком значении Н \i
максимально? Чему равно цмакс?
2307. Тонкое железное кольцо со средним диаметром
d = 50 см несет на себе обмотку из N = 800 витков с током
7 = 3,0 А. В кольце имеется поперечная прорезь ширины
6 = 2,0 мм. Пренебрегая рассеянием магнитного поля на краях
зазора, найти с помощью рис. 2.89 магнитную проницаемость
железа в этих условиях.
BJji
| 1,5 | |||||||||
| = ----•= = | |||||||||
| 1,0- | z | ||||||||
| / | |||||||||
| 2 | |||||||||
| г | |||||||||
| пи - | |||||||||
| U,J | OCHL me | агничива 1 железа. | |||||||
| 1бная приоая нам хнически uucmozL | 'ния | ||||||||
| i | |||||||||
| 7 | |||||||||
| * |
О 0,1 0,2 0,3 Ofi 0,5 0,6 Н,нА/м
Рис. 2.89
2.308. Длинный тонкий стержень из парамагнетика с восприимчивостью % и площадью поперечного сечения 5 расположен вдоль оси катушки с током. Один конец стержня находится в центре катушки, где индукция магнитного поля равна В, а другой конец - в области, где магнитное поле практически отсутствует. С какой силой катушка действует на стержень?

|
2309. В установке (рис. 2.90) измеряют с помощью весов силу, с которой парамагнитный шарик объема 7 = 41 мм3 притягивается к полюсу электромагнита М. Индукция магнитного поля на оси полюсного наконечника зависит от высоты х как В =В0ехр(-ад:2), где 50= 1,50 Тл, а = 100 м"2. Найти:
а) на какой высоте хт надо поместить
шарик, чтобы сила притяжения была мак-
Рис 2.90 симальной;
б) магнитную восприимчивость парамагнетика, если максимальная сила притяжения Fuu.c= 160 мкН.

|
2310. Небольшой шарик объема V из парамагнетика с
магнитной восприимчивостью % медленно переместили вдоль
оси катушки с током из точки, где индукция магнитного поля
равна В, в область, где магнитное поле практически отсутству
ет. Какую при этом совершили работу против магнитных сил?
2311. Длинный прямой соленоид, содер
жащий и витков на единицу длины, погру
зили наполовину в парамагнитную жид
кость (рис. 2.91). Найти магнитную силу,
действующую на единицу поверхности
жидкости, если ее магнитная восприимчи
вость равна % и через соленоид течет ток
/. Куда эта сила направлена?
Рис 291
2312. Круговой виток радиуса ас
током / расположен параллельно плоской
поверхности сверхпроводника на расстоянии / от него. Найти с помощью метода зеркальных изображений магнитную индукцию в центре витка.
2313. Тонкий прямой провод с током / расположен над
плоской поверхностью сверхпроводника на расстоянии h от
последнего. Найти с помощью метода зеркальных изображений:
а) линейную плотность тока на поверхности сверхпроводни
ка как функцию расстояния г от провода;
б) магнитную силу, действующую на единицу длины
провода.
2.6. Электромагнитная индукция. Уравнения Максвелла
• Закон электромагнитной индукции Фарадея:
g, = -d<5>ldt. (2.6а)
• В случае соленоида и тороида:
Ф = #Ф,, (2.66)
где N — число витков, Ф, — магнитный поток через каждый виток.
• Индуктивность соленоида:
2 (2.6в)
• Собственная энергия тока и взаимная энергия двух токов:
(2.6г)
• Объемная плотность энергия магнитного поля:
Плотность тока смещения:
(2.6е)
Уравнения Максвелла в дифференциальной форме:
VB-0,
где Vx = rot (ротор) и V' = div (дивергенция).
• Плотность потока электромагнитной энергии (вектор Пойнтинга) и
объемная плотность энергии электромагнитного поля:
S - [EH], w - ED/2 + ВН/2. (2.бз)
• Формулы преобразования полей при переходе от ЛГ-системы отсчета к
движущейся по отношению к ней со скоростью v0 ЛГ'-системе.
При и„ «с
| (2.6и) |
' = B-[veE]/c2.
В общем случае
Е!ГЕН»
(2.6к)
где символами II и ± отмечены составляющие полей, параллельные и перпендикулярные вектору v0.
• Инварианты электромагнитного поля:
EB = inv, E2-c2B1 = inv. (2.6л)

|
| 0_ |
Рис. 2.92
2314. Контур находится в однородном магнитном поле с индукцией В (рис. 2.92). Верхнюю часть контура -провод в виде полуокружности радиуса а - вращают с постоянной угловой скоростью ы вокруг оси ОО'. В момент t = 0 магнитный поток через контур максимальный. Найти ЭДС индукции в контуре как функцию времени t.

|
2.315. Провод, имеющий форму параболы у = кхг, находится в однородном магнитном поле с индукцией В (рис. 2.93). Из вершины параболы в момент t = 0 начали перемещать перемычку 12. Найти ЭДС индукции в образовавшемся контуре как функцию у, если перемычку перемещают:
| о |
а) с постоянной скоростью ь;
| Рис. 2.93 |
б) с постоянным ускорением а, при
чем в момент t = 0 скорость перемычки
была равна нулю.
2316. Металлический диск радиуса а = 25 см вращают с
постоянной угловой скоростью о = 130 рад/с вокруг его оси.
Найти разность потенциалов между центром и ободом диска,
если:
а) внешнего магнитного поля нет;
| —>- | |||
| — *-u | |||
б) имеется перпендикулярное диску
внешнее однородное магнитное поле с
индукцией В = 5,0 мТл.
2317. Длинный прямой проводник с
током / и П-образный проводник с
подвижной перемычкой расположены в
одной плоскости (рис. 2.94). Перемычку,
длины которой /, перемещают вправо с Рис. 2.94
| X | а |
постоянной скоростью v. Найти ЭДС индукции в контуре как функцию расстояния г.
2318. Квадратная рамка со стороной
а и длинный прямой провод с током / /
находятся в одной плоскости (рис. 2.95).
Рамку поступательно перемещают вправо
с постоянной скоростью v. Найти ЭДС
индукции в рамке как функцию расстоя- Рис. 2.95
ния х.
2319. По двум гладким вертикальным проводам, отстоящим
друг от друга на расстояние I, скользит под действием силы
тяжести проводник-перемычка массы т. Вверху провода
замкнуты на сопротивление R (рис. 2.96). Система находится в
однородном магнитном поле с индукцией В, перпендикулярном
плоскости, в которой перемещается перемычка. Пренебрегая
сопротивлением проводов, перемычки и скользящих контактов,
| R |
а также магнитным полем индукционного тока, найти установившуюся скорость перемычки.
2320. Система отличается от рассмотренной
в предыдущей задаче (см. рис. 2.96) лишь
тем, что вместо сопротивления R к концам
вертикальных проводов подключен конденса
тор емкости С. Найти ускорение перемычки.
2321. В системе, рассмотренной в задаче
2.314 (см. рис. 2.92), сопротивление контура
| Рис. 2.96 |
равно R. Пренебрегая магнитным полем индукционного тока, найти среднюю за период вращения тепловую мощность в контуре.
2322. Круговой контур, имеющий площадь S и сопротивле
ние R, вращают с постоянной угловой скоростью ы вокруг его
диаметра, который перпендикулярен однородному магнитному
полю с индукцией В. Пренебрегая магнитным полем индукци
онного тока, найти, каким моментом силы N(t) надо действо
вать на контур в этих условиях. В момент t = 0 плоскость
контура перпендикулярна направлению магнитного поля.
2323. Между полюсами электромагнита находится небольшая
катушка, ось которой совпадает с направлением магнитного
поля. Площадь поперечного сечения катушки S = 3,0 мм2, число витков N = 60. При повороте катушки на 180° вокруг ее диаметра через подключенный к ней баллистический гальванометр протекает заряд q = 4,5 мкКл. Найти индукцию магнитного поля между полюсами, если сопротивление электрической цепи R = 40 Ом.
 2324. Квадратная проволочная рам
2324. Квадратная проволочная рам
ка со стороной а и прямой проводник
с постоянным током / лежат в одной
-—. плоскости (рис. 2.97). Сопротивление I рамки R. Ее повернули на 180° вокруг оси ОО', отстоящей от проводника с током на расстояние Ъ. Найти количество электричества, протекшее в рамке.
| Рис. 2.97 |
2325. На расстояниях а и Ъ от
длинного прямого проводника с посто
янным током /0 расположены два
параллельных ему провода, замкнутых на одном конце сопротивлением R (рис. 2.98). По проводам без трения перемещают с постоянной скоростью v стержень-перемычку. Пренебре-

|
гая сопротивлением проводов и стержня, а также магнитным полем индукционного тока, найти:
а) индукционный ток в стержне;
б) силу, нужную для поддержания постоянства Скорости.
2326. Стержень 12 массы т скользит без трения по двум
длинным рельсам, расположенным на расстоянии I друг от
| 1 |
друга (рис. 2.99). На левом конце рельсы
замкнуты сопротивлением R. Система
находится в вертикальном однородном Г~
магнитном поле с индукцией В. В мо- £>\
| -е- |
мент t = О стержню сообщили вправо М
начальную скорость v0. Пренебрегая
| Рис. 2.99 |
сопротивлением рельсов и стержня, а также магнитным полем индукционного тока, найти:
а) расстояние, пройденное стержнем до остановки;
б) количество теплоты, выделенной при этом на сопротив
лении.
2327. По П-образному проводнику, расположенному в
горизонтальной плоскости, может скользить без трения пере
мычка 12 (рис. 2.100). Она имеет длину /, массу т и сопро
тивление R. Вся система находится в
вертикальном однородном магнитном поле ^
| В ® |
| г Рис. 2.100 |
с индукцией В. В момент г = 0 на перемычку стали действовать постоянной горизонтальной силой F, и перемычка начала перемещаться вправо. Найти скорость перемычки как функцию времени. Магнитное поле индукционного тока и сопротивление П-образного проводника пренебрежимо малы.
2328. Плоский контур (рис. 2.101), имеющий вид двух
квадратов со сторонами а = 20 см и Ь = 10см, находится в

|
однородном магнитном поле, перпендикулярном его плоскости. Индукцию поля меняют по закону B=Bosin<ut, где
В0=10 мТл и о) = 100 с"1. Найти амплитуду индукционного тока в контуре, если сопротивление единицы длины его р=50мОм/м. Магнитным полем этого тока пренебречь.
Рис 2Ш 2329. Плоская спирать с большим
числом витков N, плотно прилегающих
друг к другу, находится в однородном магнитном поле, перпендикулярном плоскости спирали. Наружный радиус витков спирали равен а. Индукция поля изменяется во времени но закону В =Bosina>t, где Во и «- постоянные. Найти амплитудное значение ЭДС индукции в спирали.
2330. П-образный проводник находится в однородном
магнитном поле, перпендикулярном плоскости проводника и
изменяющемся со скоростью 5=0,10Тл/с. Вдоль параллельных сторон этого проводника перемещают покоившийся
проводник-перемычку с ускорением а = 10 см/с2. Длина перемычки 1 = 20 см Найти ЭДС индукции в контуре через (= 2,0 с после начала перемещения, если в момент f = 0 площадь контура и индукция магнитного поля равны нулю.
2331. Внутри длинного соленоида находится катушка из А'
витков с площадью поперечного сечения S. Катушку поворачи
вают с постоянной угловой скоростью «вокруг оси, совпадаю
щей с ее диаметром и перпендикулярной оси соленоида. Найти
ЭДС индукции в катушке, если индукция магнитного поля в
соленоиде меняется со временем как В = Bosmc->t и в момент
t = 0 ось катушки совпадала с осью соленоида.
2332. В длинном соленоиде с радиусом сечения а и числом
витков в на единицу длины изменяют ток с постоянной
скоростью / А/с. Найти напряженность вихревого электрического
поля как функцию расстояния г от оси соленоида. Изобразить
примерный график этой зависимости.
2333. На длинный соленоид, имеющий диаметр сечения
d = 5 см и содержащий и = 20 витков на 1 см длины, плотно
надет круговой виток из медного провода сечением S = 1,0 мм2. Найти ток в витке, если ток в обмотке соленоида увеличивают
с постоянной скоростью /= 100 А/с. Магнитным полем индукционного тока пренебречь.
2334. Непроводящее тонкое кольцо массы т, имеющее
заряд q, может свободно вращаться вокруг своей оси. В
момент г = 0 включили однородное магнитное поле, перпендику
лярное плоскости кольца. Индукция поля начала нарастать по
некоторому закону В (Г). Найти угловую скорость о> кольца как
функцию В.
2335. Магнитный поток через неподвижный контур с
сопротивлением R изменяется в течение времени т по закону
Ф =at{x -t). Найти количество теплоты, выделенной в контуре
за это время. Магнитным полем индукционного тока прене
бречь.
2336. В середине длинного соленоида находится коаксиаль
ное кольцо прямоугольного сечения из проводящего материала
с удельным сопротивлением р. Толщина кольца А, его
внутренний и внешний радиусы а и Ъ. Индукцию магнитного
поля соленоида изменяют со временем по закону В = р t, где
Р - постоянная. Найти индукционный ток в кольце, пренебре
гая его магнитным полем.
2337. Сколько метров тонкого провода надо взять для
изготовления соленоида длины /0 = 100 см с индуктивностью
L = 1,0 мГн, если диаметр сечения соленоида значительно меньше его длины?
2338. Найти индуктивность соленоида длины /, обмоткой
которого является медная проволока массы т. Сопротивление
обмотки R. Диаметр соленоида значительно меньше его длины.
2339. Катушку индуктивности L = 300 мГн с сопротивлением
R = 140 мОм подключили к постоянному напряжению. Через
сколько времени ток через катушку достигает л = 50 % устано
вившегося значения?
2340. Вычислить постоянную времени т соленоида длины
/ = 100 см, имеющего однослойную обмотку из медного провода
массы т = 1,0 кг. Предполагается, что диаметр сечения соленои
да значительно меньше его длины.
Примечание. Постоянная времени т = LjR, где L -индуктивность, R - активное сопротивление.
2341. Найти индуктивность единицы длины кабеля, представ
ляющего собой два тонкостенных коаксиальных металлических
цилиндра, если радиус внешнего цилиндра в ц = 3,6 раза
больше внутреннего. Магнитную проницаемость среды между
цилиндрами считать равной единице.
2342. Определить индуктивность тороидального соленоида из
N витков, внутренний радиус которого равен Ь, а поперечное
сечение имеет форму квадрата со стороной а. Пространство внутри соленоида заполнено парамагнетиком с магнитной проницаемостью ц.

|
| Рис. 2.102 |
2.343. Вычислить индуктивность единицы длины двухпроводной ленточной линии (рис. 2.102), если расстояние между лентами h значительно меньше их ширины Ъ, а именно b/h = 50. 2344. Найти индуктивность единицы длины двухпроводной линии, если радиус каждого провода в г\ раз меньше расстояния между
их осями. Полем внутри проводов пренебречь, магнитную проницаемость всюду считать равной единицы и ц» 1.
2345. Кольцо радиуса а = 50 мм из тонкой проволоки
индуктивности L = ОДб мкГн поместили в однородное магнитное
поле с индукцией В = 0,50 мТл так, что его плоскость стала
перпендикулярной направлению поля. Затем кольцо охладили
до сверхпроводящего состояния и выключили магнитное поле.
Найти ток в кольце.
2346. Сверхпроводящее круглое кольцо радиуса а, имеющее
индуктивность L, находится в однородном магнитном поле с
индукцией В. Плоскость кольца параллельна вектору В, и ток
в кольце равен нулю. Затем плоскость кольца повернули на 90°
в положение, перпендикулярное полю. Найти:
а) ток в кольце после поворота;
б) работу, совершенную при этом.
2347. Ток /0 = 1,9 А течет по длинному замкнутому сверхпро
водящему соленоиду. Найти ток в соленоиде после того, как его
растянули, увеличив длину на ц = 5 %.
2348. Замкнутая цепь состоит из последовательно включен
ных источника постоянной ЭДС & и дросселя индуктивности
L. Активное сопротивление всей цепи равно R. В момент
t = 0 индуктивность дросселя скачком уменьшили в ц раз.
Найти ток в цепи как функцию времени X.
Указание. При скачкообразном изменении индуктивности полный магнитный поток (потокосцепление) остается неизменным.
| ■ К |
| ■± R\ R |
2349. Найти закон изменения во вк мени тока, текущего через индуктивнос'1 L в схеме (рис. 2.103) после замыкания ключа К в момент Г = 0.
| Рис. 2.103 |

|
2.350. В схеме (рис. 2.104) известны ЭДС % источника, сопротивление R и индуктивности катушек L, и L2. Внутреннее сопротивление источника и сопротивления катушек пренебрежимо малы. Найти установившиеся токи в катушках после замыкания ключа К.
| Рис. 2.104 |

|
| I |
2351. Два длинных коаксиальных со
леноида содержат пх и пг витков на
единицу длины. Внутренний соленоид,
имеющий площадь поперечного сечения
S, заполнен магнетиком проницаемости ц.
Найти взаимную индуктивность соленои
дов в расчете на единицу их длины.
2352. Вычислить взаимную индуктив
ность длинного прямого провода и прямо
угольной рамки со сторонами а и Ъ. Рамка и прямой провод
лежат в одной плоскости, причем ближайшая к проводу
сторона рамки длины Ъ параллельна проводу и отстоит от него
на расстояние I.
2353. Определить взаимную индуктивность тороидальной
катушки и проходящего по ее оси бесконечного прямого
провода. Катушка имеет прямоугольное сечение, ее внутренний
радиус а, внешний Ь. Длина стороны поперечного сечения то
ра, параллельная проводу, равна h. Число витков катушки N.
Система находится в однородном магнетике проницаемости ц.
2354. На поверхность тора квадратного
сечения равномерно навито JVj витков
тонкой проволоки. На эту обмотку в свою
очередь навито N2 витков, как показано на
рис. 2.105. Внутренний и внешний радиусы
тора равны а и Ъ. Найти взаимную индук
тивность обеих обмоток.
2355. Два концентрических тонких про
водника в форме окружностей с радиусами а
и Ъ лежат в одной плоскости. Имея в виду,
что а «Ь, найти:
| Рис. 2.105 |
а) из взаимную индуктивность;
б) магнитный поток через поверхность, натянутую на внешний проводник, если по внутреннему проводнику течет ток /. 2356. Два одинаковых контура в виде равносторонних треугольников (из тонких проводов с изоляцией) одной

|
стороной совмещены, а расстояние между противоположными вершинами равно стороне треугольников. Индуктивность каждого контура!. Найти их взаимную индуктивность.
| Рис, 2.1(16 |
2357. Ток / течет по рамке в виде квадратного контура со стороной а. Найти магнитный поток через полуплоскость Р (рис. 2.106), граница которой 00' отстоит от ближайшей стороны рамки на расстояние Ь. Полуплоскость Р и рамка лежат в одной плоскости.
Указание. Воспользоваться теоремой взаимности: L12 = L21.
2358. Имеется тонкое кольцо радиуса а с током /. Найти индукцию магнитного поля в плоскости кольца в точке, находящейся на расстоянии г от его центра, если г»а.

|
| Рис 2.107 |
2.359. Небольшой цилиндрический магнит М (рис. 2.107) находится в центре тонкой катушки радиуса а, состоящей из N витков. Катушка подключена к баллистическому гальванометру. Сопротивление всей
цепи равно R. Найти магнитный момент магнита, если при его удалении из катушки через гальванометр прошло количество электричества q.
Дата добавления: 2015-08-02; просмотров: 1514 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| А) 1-7; б) 1-2; в) 1-3. Сопротивление каждого ребра каркаса равно R. | | | Механические колебания |