
Читайте также:
|
где
Затухающие колебания контура:
q =^me"''cos((i) t + а),
(3.2 a)
• Логарифмический декремент затухания А. и добротность Q контура определяются формулами (3.1 г). При слабом затухании:
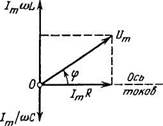
• Установившиеся вынужденные колебания при последовательном включении в контур напряжения V= Umcosu)f.
/ = /mCOS(wf -ф), (3.2 в)
где
| о>С |
ыЬ - ■
(3.2 г)
Соответствующая векторная диаграмма напряжений показана на рис. 3.26. • Полное сопротивление (импеданс):
|
z=v/F7F, (з.2 д)
где X = XL - Хс — реактивное сопротивление. • Мощность, выделяемая в цепи пере-
менного тока:
(3.2 е)
где U и 1 — действующие (эффективные) значения напряжения и тока:
| Рис. 3.26 |
U=UJs/2, I'Ims/2. (3.2ж)
3.111. Небольшой шарик массы т=21 г, подвешенный на
нерастяжимой изолирующей нити на высоте А = 12 см от
горизонтальной проводящей плоскости, совершает малые
колебания. После того как ему сообщили заряд q, период
колебаний изменился в т) = 2,0 раза. Найти q.
3.112. Небольшая магнитная стрелка совершает малые
колебания вокруг оси, перпендикулярной направлению внешнего
магнитного поля. При изменении индукции этого поля период колебаний стрелки уменьшился в ц =5,0 раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний пренебрежимо мало.
|
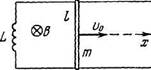
3.113. Контур (рис. 3.27) обра
зован двумя параллельными про
водниками, замыкающим их соле
ноидом с индуктивностью L и
проводящим стержнем массы т,
который может без трения сколь-
Рис 3.27 зить по проводникам. Проводники
расположены в горизонтальной
плоскости в однородном вертикальном магнитном поле с индукцией В. Расстояние между проводниками I. В момент г = 0 стрежню сообщили начальную скорость vg. Найти закон его движения x(t). Сопротивление контура пренебрежимо мало.
3.114. Катушка индуктивности L соединяет верхние концы
двух вертикальным медных шин, отстоящих друг от друга на
расстояние /. Вдоль шин падает без начальной скорости
горизонтальный проводник-перемычка массы т (без нарушения
контакта с шинами). Вся система находится в однородном
магнитном поле с индукцией В, перпендикулярном плоскости
шин. Найти закон движения проводника x(t). Сопротивление
всех проводников пренебрежимо мало.
3.115. Ток в колебательном контуре зависит от времени как
/ = /msin(wfl0., где 1т = 9,0 мА, ыо =4,5 -104с''. Емкость конденсатора С = 0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент t = Q.
3.116. В контуре, состоящем из конденсатора емкости С и
катушки индуктивности L, совершаются свободные незатухаю
щие колебания, при которых амплитуда напряжения на
конденсаторе равна Um. Найти связь между током / в контуре
и напряжением U на конденсаторе.
3.117. Колебательный контур состоит из конденсатора
емкости С, катушки индуктивности L с пренебрежимо малым
сопротивлением и ключа. При разомкнутом ключе конденсатор
зарядили до напряжения Um и затем в момент f = 0 замкнули
ключ. Найти:
а) ток в контуре как функцию времени;
б) ЭДС самоиндукции в катушке в моменты, когда электрическая энергия конденсатора равна энергии тока в катушке.
3.118. Найти максимальный ток в цепи (рис. 2.28) и
максимальное напряжение на конденсаторе после замыкания
ключа К. Активное сопротивление цепи пренебрежимо мало.
3.119. В контуре, состоящем из плоского конденсатора и
катушки индуктивности с пренебрежимо малым активным
сопротивлением, происходят колебания с энергией W. Пласти
ны конденсатора медленно раздвинули так, что частота
колебаний увеличилась в т) раз. Какую работу совершили при
этом против электрических сил?
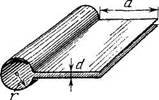
3.120. Найти собственную частоту ы0 резонатора (рис. 3.29),
считая, что его плоская часть является конденсатором, а
цилиндрическая - индуктивностью. Необходимые размеры
указаны на рисунке.
К
Рис. 3.28
Рис. 3.29

|
| Рис. 3.30 |
3.121. На рис. 3.30 показано
сечение тороидального резонато
ра, используемого во многих
микроволновых генераторах.
Считая, что центральная часть
резонатора является плоским
конденсатором, а тороидальная
полость — индуктивностью, оце
нить собственную частоту резо
натора. Необходимые размеры даны на рисунке.
3.122. В колебательном контуре (рис. 3.31) индуктивность
катушки L - 2,5 мГн, а емкости конденсаторов Ct = 2,0 мкФ и
С2 = 3,Омкф. Конденсаторы зарядили до напряжения (7=1805
и замкнули ключ К. Найти:
а) период собственных колебаний;
б) амплитудное значение тока через катушку.
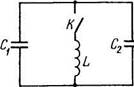
3.123. Электрическая цепь (рис. 3.32) имеет пренебрежимо малое активное сопротивление. Левый конденсатор зарядили до напряжения Uo и затем - в момент t = 0 - замкнули ключ
К. Найти зависимость от времени Г напряжений на обоих конденсаторах.

|
|
Рис. 3.31
Рис. 3.32
3.124. Контур состоит из катушки индуктивности L и
конденсатора емкости С. Сопротивление катушки и проводов
пренебрежимо мало. Катушка находится в постоянном магнит
ном поле, так что суммарный поток, пронизывающий все витки
катушки, равен Ф. В момент t = 0 магнитное поле выключили.
Считая время выключения очень малым по сравнению с
периодом собственных колебаний контура, найти ток в контуре
как функцию времени t.
3.125. В контуре совершаются свободные затухающие
колебания, при которых напряжение на конденсаторе меняется
во времени по закону U = l/me'prcosw Г. Найти моменты времени, когда модуль напряжения на конденсаторе достигает:
а) амплитудных значений;
б) максимальных (экстремальных) значений.
3.126. Контур содержит конденсатор емкости С, катушку с
индуктивностью L и активным сопротивлением R, а также
ключ. При разомкнутом ключе конденсатор зарядили, после
чего ключ замкнули, и начались колебания. Найти отношение
напряжения на конденсаторе к его амплитудному значению в
момент непосредственно после замыкания ключа.
3.127. В контуре с емкостью С и индуктивностью L
происходят свободные затухающие колебания, при которых ток
меняется во времени по закону / = /me"^'sinwf. Найти напряжение на конденсаторе в зависимости от времени и в момент
3.128. Контур состоит из конденсатора емкости С = 4,0 мкФ и
катушки с индуктивностью L = 2,0 мГн и активным сопро
тивлением R = 10 Ом. Найти отношение энергии магнитного
поля катушки к энергии электрического поля конденсатора в
момент максимума тока.
3.129. Контур содержит две последовательно соединенные
катушки с активными сопротивлениями Rt и ^ и индуктив-
ностями L, и L2, причем взаимная индуктивность их пренебре
жимо мала. Эти катушки надо заменить одной так, чтобы
частота и добротность контура не изменились. Найти индуктив
ность и активное сопротивление такой катушки.
3.130. Найти время, за которое амплитуда колебаний тока в
контуре с добротностью Q = 5000 уменьшится в т) = 2,0 раза,
если частота колебаний v = 2,2 МГц.
3.131. Колебательный контур имеет емкость С = 10 мкФ,
индуктивность L = 25 мГн и активное сопротивление R = 1,0 Ом.
Через сколько колебаний амплитуда тока в этом контуре
уменьшится в е раз?
3.132. На сколько процентов отличается частота ы свобод
ных колебаний контура с добротностью Q = 5,0 от собственной
частоты ы0 колебаний этого контура?
3.133. Проводник в форме квадратной рамки
со стороной а, подвешенный на упругой нити,
находится в однородном горизонтальном маг
нитном поле с индукцией В. В положении
равновесия плоскость рамки параллельна
вектору В (рис. 3.33). Будучи выведана из
положения равновесия, рамка совершает малые ■
колебаний вокруг вертикальной оси, проходящей
через ее центр. Момент инерции рамки относи
тельно этой оси /, ее электрическое сопротивле- Рис. з.зз
ние R. Пренебрегая индуктивностью рамки,
найти время, через которое амплитуда ее углового поворота уменьшится в е раз.
3.134. В схеме (рис. 3.34) ЭДС элемента #"=2,0 В, его
внутреннее сопротивление г = 9,0 Ом, емкость конденсатора
С = 10 мкФ, индуктивность катушки L = 100 мГн и активное
сопротивление R = 1,0 Ом. В некоторый момент ключ К
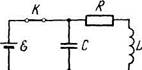
|
разомкнули. Найти энергию колебаний в контуре:
а) непосредственно после размыка
ния ключа;
б) через t = 0,30 с после размыка
ния ключа.
Рис. 3.34 3.135. В контуре, добротность кото-
рого Q = 50 и собственная частота
колебаний v0 = 5,5 кГц, возбуждаются затухающие колебания. Через сколько времени энергия, запасенная в контуре, уменьшится в т) =2,0 раза?
3.136. Колебательный контур содержит конденсатор с утечкой.
Емкость конденсатора С, его активное сопротивление R.
Индуктивность катушки L. Сопротивление катушки и проводов
пренебрежимо мало. Найти:
а) частоту затухающих колебаний такого контура;
б) его добротность.
3.137. Найти добротность контура с емкостью С = 2,0 мкФ и
индуктивностью L = 5,0 мГн, если на поддержание в нем
незатухающих колебаний с амплитудой напряжения на конден
саторе Um ■ 1,0 В необходимо подводить мощность {Р) = 0,10 мВт.
Затухание колебаний в контуре достаточно мало.
3.138. Какую среднюю мощность должен потреблять колеба
тельный контур с активным сопротивлением R = 0,45 Ом, чтобы
в нем поддерживались незатухающие гармонические колебания
с амплитудой тока /м = 30 мА?
3.139. Колебательный контур содержит конденсатор емкостью
С = 1,2 нФ и катушку с индуктивностью L = 6,0 мкГн и активным
сопротивлением Л =0,50 Ом. Какую среднюю мощность нужно
подводить к контуру, чтобы поддерживать в нем незатухающие
гармонические колебания с амплитудой напряжения на
конденсатора Um = 10 В?
3.140. Найти частоту затухающих колебаний контура,
показанного на рис. 3.35. Емкость С, индуктивность L и
активное сопротивление R предполагаются известными.
3.141. Имеются два колебательных контура (рис. 3.36) с
конденсаторами одинаковой емкости. При каком соотношении
между индуктивностями и активными сопротивлениями катушек
частоты и затухания свободных колебаний в обоих контурах
будут одинаковыми? Взаимная индуктивность катушек левого контура пренебрежимо мала.
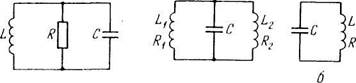
А
Рис. 3.35 Рис. 3.36
3.142. Контур состоит из последовательно включенных
конденсатора емкости С, катушки индуктивности L, ключа и
сопротивления, равного критическому для данного контура. При
разомкнутом ключе конденсатор зарядили до напряжения Uo
и в момент t = 0 ключ замкнули. Найти ток 1 в контуре как
функцию времени t. Чему равен /макс?
3.143. Катушку с активными сопротивлением R и индуктив
ностью L подключили в момент t = 0 к источнику напряжения
U = UMcosu>t. Найти ток в катушке l(t).
3.144. Цепь, состоящую из последовательно соединенных
конденсатора емкости С и сопротивления R, подключили к
неременному напряжению J7=f/Mcoswf в момент f = 0. Найти
ток в цепи как функцию времени t.
3.145. Длинный однослойный соленоид из проволоки с
удельным сопротивлением р имеет на единицу длины п
плотно расположенных витков. Толщина изоляции провода
пренебрежимо мала. Радиус сечения соленоида равен а. Найти
разность фаз между током и переменным напряжением частоты
v, которое подключено к концам соленоида.
3.146. Концы цепи, состоящей из последовательно включен
ных конденсатора и активного сопротивления R = 110 Ом,
подсоединили к переменному напряжению с амплитудой
Um = ПО В. При этом амплитуда установившегося тока в цепи
1т = 0,50 А. Найти разность фаз между током и подаваемым
напряжением.
R
| I X |
| и' |
| U |
3.147. На рис. 3.37 показана простейшая схема сглаживающего фильтра. На вход подают напряжение Uo = [1 + cos <of]. Найти:
а) выходное напряжение V (О;
| Рис. 3.37 |
б) значение RC, при котором амплитуда
переменной составляющей напряжения на
выходе будет в т) = 7,0 раз меньше постоян
ной составляющей, если «= 314с"1.
3.148. Колебательный контур с индуктивностью L подключен
последовательно к внешнему синусоидальному напряжению с
амплитудой Un. Контур настроен в резонанс, при котором
амплитуда установившегося тока равна 1т. Найти промежуток
времени х, за который амплитуда тока уменьшится в е раз, если процесс будет происходить в режиме свободных затухающих колебаний.
3.149. Изобразить примерные векторные диаграммы напряже
ний в электрических цепях, показанных на рис. 3.38 а, б.
Внешнее напряжение U предполагается гармоническим с
частотой ы.
|
| L.R |
ш<ш0
А
Рис. 3.38
3.150. Цепь из последовательно соединенных конденсатора
емкости С = 22 мкФ и катушки с активным сопротивлением
R = 20 Ом и индуктивностью L = 0,35 Гн подключена к сети
переменного напряжения с амплитудой Um = 180 В и частотой
w =314 с"1. Найти:
а) амплитуду тока в цепи;
б) разность фаз между током и внешним напряжением;
в) амплитуды напряжения на конденсаторе и катушке.
3.151. Цепь из последовательно соединенных конденсатора
емкости С, катушки индуктивности L (без активного сопротив-
ления) и резистора с сопротивлением R подключили к источнику гармонического напряжения, частоту ы которого можно менять, не изменяя его амплитуды. Найти частоту ы, при которой становится максимальным напряжение:
а) на конденсаторе; б) на катушке.
Убедиться, что эти частоты связаны соотношениями
ЫСР«. < Wtp«И WCpM ' WLp«= «О-
3.152. Переменное напряжение с частотой ы=314с"1 и
амплитудой Um = 180 В подключено к концам цепи, состоящей
из последовательно соединенных конденсатора и катушки с
активным сопротивлением R = 40 Ом и индуктивностью
L = 0,36 Гн. При каком значении емкости конденсатора амплиту
да напряжения на катушке будет максимальной? Чему равна
эта амплитуда и соответствующая амплитуда напряжения на
конденсаторе?
3.153. Конденсатор емкости С, пространство между обкладка
ми которого заполнено слабо проводящей средой с активным
сопротивлением R, подключили к источнику переменного
напряжения U = Umcoswt. Найти установившийся ток в
подводящих проводах в зависимости от времени. Сопротивле
ние проводов пренебрежимо мало.
3.154. Колебательный контур содержит конденсатор емкости
С и соленоид с индуктивностью L,. Соленоид индуктивно
связан с короткозамкнутой катушкой, имеющей индуктивность
L2 и пренебрежимо малое активное сопротивление. Их взаим
ная индуктивность L12. Найти собственную частоту данного
колебательного контура.
3.155. Найти добротность колебательного контура, в который
последовательно включен источник переменной ЭДС, если при
резонансе напряжение на конденсаторе в п раз превышает
напряжение на источнике.
3.156. Цепь переменного тока, состоящая из последовательно
соединенных катушки и конденсатора, подключена к источнику
переменной ЭДС, причем индуктивность катушки подобрана так,
что ток в цепи максимален. Найти добротность системы, если
известно, что при увеличении индуктивности в п раз ток в
цепи уменьшается в т) раз.
3.157. Последовательно соединенные конденсатор емкости
С = 45 мкФ и катушка с активным сопротивлением подключены
к источнику гармонического напряжения, частоту которого
можно менять, не изменяя его амплитуды. При частотах
vx = 1,50 кГц и v2= 2,50 кГц амплитуда тока оказалась одинако
вой. Найти индуктивность катушки.
3.158. Показать, что при малом затухании добротность
контура, в котором совершаются вынужденные колебания,
Q»(д>0/ Д W, где (д>0 — собственная частота колебаний, Ды -
ширина резонансной кривой /(ы) на "высоте", в \J2 раз меньшей амплитуды тока при резонансе.
3.159. К концам цепи, состоящей из последовательно
соединенных конденсатора и катушки, подают поочередно два
переменных напряжения одинаковой амплитуды, но разной
частоты. Частота одного напряжения равна собственной частоте
(ы0), другого - в Ti раз больше. Найти отношение амплитуд
токов /0//, возбуждаемых обоими напряжениями, если доброт
ность системы равна Q. Вычислить это отношение для<? = 10
и 100, если ц =1,10.
3.160. Для зарядки аккумулятора постоянным током /0
требуется t0 часов. Сколько времени понадобится для зарядки
такого аккумулятора от сети через однополупериодныи выпря
митель, если действующее значение тока тоже равно /0.
|
3.161. Найти действующее значение тока, если среднее значение его равно /0, а сам ток зависит от времени по закону:
а) показанному на рис. 3.39;
б) /*?|sin(cdr)|-
Рис. 3.39 3.162. Соленоид с индуктив-
ностью 1 = 7 мГн и активным сопротивлением R = 44 Ом подключили сначала к источнику постоянного напряжения Uo, а затем к генератору синусоидального напряжения с действующим значением U = U0. При какой частоте генератора мощность, потребляемая соленоидом, будет в rj = 5,0 раза меньше, чем в первом случае?
3.163. К сети с действующим напряжением U = 100 В подключили катушку, индуктивное сопротивление которой 3^ = 30 Ом и импеданс Z = 50Om. Найти разность фаз между
током и напряжением, а также тепловую мощность, выделяемую в катушке,
3.164. Катушка с индуктивностью L = 0,70 Гн и активным
сопротивлением г = 20 Ом соединена последовательно с безын
дукционным сопротивлением R, и между концами этой цепи
приложено переменное напряжение е действующим значением
£/ = 220 13 и частотой «=314с"1. При каком значении сопротивления R в цепи будет выделяться максимальная тепловая мощность? Чему она равна?
3.165. Цепь, состоящая из последовательно соединенных
конденсатора и катушки, подключена к сети. Изменив емкость
конденсатора, добились увеличения выделяемой тепловой
мощности в катушке в л = 1,7 раза. На сколько процентов
изменилось при этом значение cos<p?
3.166. В колебательный контур с добротностью Q = 100
включен последовательно источник синусоидальной ЭДС с
постоянной амплитудой напряжения. При некоторой частоте
внешнего напряжения тепловая мощность, выделяемая в
контуре оказывается максимальной. На сколько процентов
следует изменить эту частоту, чтобы выделяемая мощность
уменьшилась в п =2,0 раза?
3.167. Цепь, состоящую из последовательно соединенных
безындукционного сопротивления R =0,16 кОм и катушки с
активным сопротивлением, подключили к сети с действующим
напряжением U ■- 220 В. Найти тепловую мощность, выделяемою
па катурже, если действующие напряжения, на сопротивлении/?
и катушке равны соответственно Ul = 80 В и Ь\ - 180 В.
3.168. Катушка и безындукционное сопротивление R -25 Ом
подключены параллельно к сети передюнного напряжения.
Найти тепловую мощность, выделяемую в катушке, если из
сети потребляется ток /-0,90 А, а через катушку и сопротивле
ние R текут токи соответственно. 7,-0,50 А и /2=О,6ОА.
3.169. Найти полное сопротивление участка цени, состоящего
из параллельно включенного конденсатора емкости С-73мкФ
и активного сопротивления R ■- 100 Ом, для переменного тока
частоты «= 314 с"1.
3.170. Изобразить примерные векторные диаграммы токов в
электрических контурах, показанных на рис. 3.40. Предполагает
ся, что подаваемое между точками Л и В напряжение синусои-
дальное и параметры каждого контура подобраны так, что суммарный ток /0 через контур отстает по фазе от внешнего напряжения на угол <р.
|
|
С
Hh
L.R
6 Рис. 3.40
В
3.171. Конденсатор емкости С = 1,0 мкФ и катушку с актив
ным сопротивлением R = 0,10 Ом и индуктивностью L = 1,0 мГн
подключили параллельно к источнику синусоидального напря
жения с действующим значением U = 31 В. Найти:
а) частоту w, при которой наступает резонанс;
б) действующее значение подводимого тока при резонансе
и соответствующие токи через катушку и конденсатор.
3.172. К источнику синусоидального напряжения с частотой о
подключили параллельно конденсатор емкости С и катушку с
активным сопротивлением R и индуктивностью L. Найти
разность фаз между подводимым к контуру током и напряжени
ем на источнике.
3.173. Участок цепи состоит из параллельно включенных
конденсатора емкости С и катушки с активным сопротивлением/?
и индуктивностью L. Найти полное сопротивление этого участка
для переменного напряжения с частотой w.
3.174. Кольцо из тонкого провода с активным сопротивлени
ем R и индуктивностью L вращают с постоянной угловой
скоростью W во внешнем однородном магнитном поле,
перпендикулярном к оси вращения. При этом поток магнитной
индукции внешнего поля через кольцо изменяется во времени
по закону Ф = Ф0созо>*. Показать, что индукционный ток в
кольце зависит от времени как / = /msin(wf - <p), где
 1т = и> Фо/yR2 + u>2L2, причем tg<p=u>L/R.
1т = и> Фо/yR2 + u>2L2, причем tg<p=u>L/R.

|
| Рис. 3.41 |
3.175. Найти среднюю механическую мощность, развиваемую
внешними силами для поддержания вращения кольца из
предыдущей задачи с постоянной угловой скоростью.
3.176. На деревянный сердеч
ник (рис. 3.41) надеты две ка
тушки: катушка 1 с индуктив
ностью L, и замкнутая накорот
ко катушка 2 с активным сопро
тивлением R и индуктивностью
L2. Взаимная индуктивность
катушек зависит от расстояния
х между ними по закону Ln{x),
Найти среднее значение силы взаимодействия между катушками, когда по катушке 1 течет ток /j=/0coswf.
Дата добавления: 2015-08-02; просмотров: 1250 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Механические колебания | | | Упругие волны. Акустика 1 страница |