
|
Читайте также: |
• Напряженность электрического поля у поверхности проводника в вакууме:
£„=о/е0. (2.2а)
• Поток поляризованности Р через замкнутую поверхность:
$PdS = -q', (2.26)
где q' — алгебраическая сумма связанных зарядов внутри этой поверхности.
• Вектор D (электрическое смещение) и теорема Гаусса для него:
D = eeB + P, fl)dS = q, (2.2в)
где q — алгебраическая сумма сторонних зарядов внутри замкнутой поверхности.
• Условия на границе раздела двух диэлектриков:
'«.-Л.-»'. D7n-Dln=o, E2,*EU, (2.2г)
где а' и о — поверхностные плотности связанных и сторонних зарядов, а орт нормали и направлен из среды 1 в среду 2.
• Для изотропных диэлектриков:
Р = хе0Е, D = se0E, г=1 + х. (2.2д)
• В случае изотропного однородного диэлектрика, заполняющего все
пространство между эквипотенциальными поверхностями:
В = Е0/е. (2.2е)
2.59. Небольшой шарик висит над горизонтальной проводя
щей плоскостью на изолирующей упругой нити жесткости х.
После того, как шарик зарядили, он опустился на х см, и его
расстояние от проводящей плоскости стало равным /. Найти
заряд шарика.
2.60. Электрон вылетел по нормали с плоской поверхности
проводника в вакуум, где создано однородное ускоряющее
электрическое иоле с напряженностью £=100 В/м. Имея в виду
силы электрического изображения, найти, на каком расстоянии/
от поверхности проводника скорость электрона минимальна.
2.61. Точечный заряд q = 100 мкКл находится на расстоянии
/ = 1,5 см от проводящей плоскости. Какую работу надо совер
шить против электрических сил, чтобы медленно удалить этот
заряд на очень большое расстояние от плоскости?
2.62. Два точечных заряда, q n -q, расположены на рас
стоянии / друг от друга и на одинаковом расстоянии //2 от
проводящей плоскости с одной стороны от нее. Найти модуль
электрической силы, действующей на
4°------------ 1~^ каждый заряд.
| \ I___ |
2.63. Три разноименных точечных
О j заряда расположены в вершинах квадрата
с диагональю / = 50 см, как показано на
рис. 2.8, где точка О - центр квадрата,
7 АОВ — прямой угол, образованный двумя
о проводящими полуплоскостями. Найти
силу, действующую на заряд -q, если
Рис. 2.8 |, Тг
q = 11 мкКл.
2.64. Точечный заряд q = 2,00 мкКл находится между двумя
проводящими взаимно перпендикулярными полуплоскостями.
Расстояние от заряда до каждой полуплоскости 1 = 5,0 см. Найти
модуль силы, действующей на заряд.
2.65. Точечный диполь с электрическим моментом р на
ходится на расстоянии I от проводящей плоскости. Найти силу,
действующую на диполь, если вектор р перпендикулярен
плоскости.
2.66. Точечный заряд q находится на расстоянии / от
проводящей плоскости. Определить поверхностную плотность
зарядов, индуцированных на плоскости, как функцию расстоя
ния г от основания перпендикуляра, опущенного из заряда на
плоскость.
2.67. Прямая бесконечно длинная нить имеет заряд X на
единицу длины и расположена параллельно проводящей
плоскости на расстоянии I от нее. Найти:
а) модуль силы, действующей на единицу длины нити;
б) распределение поверхностной плотности заряда о (л) на
плоскости (здесь х - расстояние от прямой на плоскости, где
а максимально).
2.68. Очень длинная нить расположена перпендикулярно
проводящей плоскости и не доходит до нее на расстояние *'. Нить заряжена равномерно с линейной плотностью А. Пусть точка О — след нити на плоскости. Найти поверхностную плотность заряда на плоскости:
а) в точке О;
б) в зависимости от расстояния г до точки О
2.69. Тонкое проволочное кольцо радиуса R = 7,5 см имеет
заряд 4 = 5,2 мкКл. Кольцо расположено параллельно проводя
щей плоскости на расстоянии / = 6,0 см от нее. Найти повер
хностную плотность заряда в точке плоскости, расположенной
симметрично относительно кольца.
2.70. Найти потенциал незаряженной проводящей сферы, вне
которой на расстоянии / = 30 см от ее центра находится
точечный заряд #=0,50мкКл.
2.71. Заряд q = 2,5 нКл распределен неравномерно по тонкому
кольцу радиуса Я =7,5 см. На расстоянии / = 100 мм от центра
кольца на его оси расположен центр проводящей незаряженной
сферы. Найти ее потенциал.
2.72. Точечный заряд q = 3,4 нКл находится на расстоянии
г = 2,5 см от центра О незаряженного сферического слоя
проводника, радиусы которого 1^ = 5,0 см и Л^ 8,0 см. Найти
потенциал в точке О.
2.73. Система состоит из двух концентрических проводящих
сфер. На внутренней сфере радиуса а находится положительный
заряд qv Какой заряд qt следует поместить на внешнюю сферу
радиуса Ь, чтобы потенциал внутренней сферы стал ф = 0? Как
будет зависеть при этом ф от расстояния г до центра системы?
Изобразить примерный график <р (г).
2.74. Четыре большие металличес- __________
кие пластины расположены на ма- /' ?
лом расстоянии d друг от друга I----------------- q j
(рис. 2.9). Внешние пластины соеди- ^---------------- — 4
нены проводником, а на внутренние
пластины подана разность потенциа- РИС. 2.9
лов Дф. Найти:
а) напряженность электрического поля между пластинами;
б) суммарный заряд на единицу площади каждой пластины.
_________ 2.75. Между пластинами накоротко
______________ замкнутого плоского конденсатора нахо-
' ^ q дится металлическая пластина с заря-
■———-—-————• дом q (рис. 2.10). Пластину перемести-
Рис. 2.Ю ли на расстояние Л Какой заряд Д#
прошел при этом по закорачивающему проводнику? Расстояние между пластинами конденсатора d.
2.76. Две проводящие плоскости 1 и 2 расположены на
расстоянии / друг от друга. Между ними на расстоянии х от
плоскости 1 находится точечный заряд q. Найти заряды,
наведенные на каждой из плоскостей.
2.77. Найти электрическую силу, которую испытывает заряд,
приходящийся на единицу поверхности произвольного провод
ника, в точке, где о = 46 мкКл/м2.
2.78. Металлический шарик радиуса R = 1,5 см имеет заряд
q = 10 мкКл. Найти модуль результирующей силы, которая
действует на заряд, расположенный на одной половине шарика.
2.79. Незаряженный проводящий шар радиуса R поместили
во внешнее однородное электрическое поле, в результате чего
на поверхности шара появился индуцированный заряд с
поверхностной плотностью a=a0cos0, где ao — постоянная,
Ь — полярный угол. Найти модуль результирующей электрической силы, которая действует на весь индуцированный заряд одного знака.
2.80. Найти энергию упругого диполя с поляризованностью
Р (р = Ре0Е) во внешнем электрическом поле с напряжен
ностью Е.
2.81. Неполярная молекула с поляризуемостью р находится
на большом расстоянии I от полярной молекулы с элетричес-
ким моментом р. Найти модуль силы взаимодействия этих
молекул, если вектор р ориентирован вдоль прямой, проходя
щей через обе молекулы.
2.82. На оси тонкого равномерно заряженного кольца радиуса
R находится неполярная молекула. На каком расстоянии х от
центра кольца модуль силы F, действующей на данную
молекулу:
а) равен нулю; б) имеет максимальное значение? Изобразить примерный график зависимости Fz(x).
2.83. Точечный сторонний заряд q находится в центре шара
из однородного диэлектрика с проницаемостью е. Найти
поляризованность Р как функцию радиуса-вектора г относитель
но центра шара, а также связанный заряд q' внутри сферы,
радиус которой меньше радиуса шара.
2.84. Точечный сторонний заряд q находится в центре
диэлектрического шара радиуса а с проницаемостью ej. Шар
окружен безграничным диэлектриком с проницаемостью е2.
Найти поверхностную плотность связанных зарядов на границе
раздела этих диэлектриков.
2.85. Показать, что на границе однородного диэлектрика с
проводником поверхностная плотность связанных зарядов
о' = -о(е -1)1 г, где с - диэлектрическая проницаемость, о -
поверхностная плотность зарядов на проводнике.
2.86. Проводник произвольной формы, имеющий заряд
q = 2,5 мкКл, окружен слоем однородного диэлектрика с прони
цаемостью е = 5,0. Найти суммарные поверхностные связанные
заряды на внутренней и наружной поверхностях диэлектрика.
2.87. В некоторой точке А внутри однородного диэлектрика
с проницаемостью е = 2,5 плотность стороннего заряда р =
= 50 мКл/м3. Найти в этой точке плотность связанных зарядов.
2.88. Однородный диэлектрик имеет вид сферического слоя
радиусов а и Ь, причем а<Ь. Изобразить примерные графики
модуля напряженности электрического поля Е и потенциала <р
как функций расстояния г от центра системы, если диэлектрик
имеет положительный сторонний заряд, распределенный
равномерно:
а) по внутренней поверхности слоя; б) по объему слоя.

|
2.89. Вблизи точки А (рис. 2.11) грани
цы раздела стекло - вакуум напряжен
ность электрического поля в вакууме
Ео= 10,0 В/и, причем угол между вектором
Ео и нормалью п к границе раздела
ао=ЗО°. Найти напряженность Е поля в
стекле вблизи точки А, угол а между
векторами Е и п, а также поверхностную
Рис 2 11
плотность связанных зарядов в точке А.
2.90. Диэлектрик с проницаемостью е граничит с вакуумом.
На его поверхности имеются сторонние заряды с плотностью а.
У поверхности диэлектрика в вакууме напряженность электри
ческого поля равна Е, причем вектор Е составляет такой угол
Ь с нормалью к поверхности раздела, что линии вектора Е не
терпят излома при переходе границы раздела. Найти угол Ь.
Каков должен быть знак а?
2.91. У плоской поверхности однородного диэлектрика с
проницаемостью е напряженность электрического поля в
| г |
 вакууме равна Ео, причем вектор Ео составляет угол Ь с нормалью к поверхности диэлектрика (рис. 2.12). Считая поле внутри и вне диэлектрика однородным, найти:
вакууме равна Ео, причем вектор Ео составляет угол Ь с нормалью к поверхности диэлектрика (рис. 2.12). Считая поле внутри и вне диэлектрика однородным, найти:
| Рис. 2.12 |
а) поток вектора Е через
сферу радиуса R с центром на
поверхности диэлектрика;
б) циркуляцию вектора D
по контуру Г длины / (см. рис. 2.12), плоскость которого перпендикулярна поверхности диэлектрика и параллельна вектору Ео.
2.92. Бесконечно большая пластина из однородного ди
электрика с проницаемостью е заряжена равномерно сторонним
зарядом с объемной плотностью р. Толщина пластины 2d.
Найти:
а) модуль напряженности электрического поля и потенциал
как функции расстояния / от середины пластины (потенциал
в середине пластины Ф = 0); взяв ось х перпендикулярно
пластине, изобразить примерные графики зависимостей
проекции Ех(х) и потенциала ф(х);
б) поверхностную и объемную плотности связанного заряда.
2.93. Сторонние заряды равномерно распределены с объем
ной плотностью р > 0 по шару радиуса R из однородного
изотропного диэлектрика с проницаемостью е. Найти:
а) модуль напряженности электрического поля как функцию
расстояния г от центра шара; изобразить примерные графики
зависимостей Е(г) и ф (г);
б) объемную и поверхностную плотности связанных зарядов.
2.94. Круглый диэлектрический диск радиуса R и толщины
d поляризован статически так, что поляризованность, равна Р,
всюду одинакова и вектор Р лежит в плоскости диска. Найти
напряженность Е электрического поля в центре диска, если
d«R.
2.95. При некоторых условиях поляризованность безгранич
ной незаряженной пластины из диэлектрика имеет вид Р -
= P0(l -x2jd2), где Ро — вектор, перпендикулярный пластине, х -
расстояние от середины пластины, d - ее полутолщина. Найти
напряженность электрического поля внутри пластины и разность
потенциалов между ее поверхностями.
2.96. Первоначально пространство между обкладками плоского конденсатора заполнено воздухом и напряженность электрического поля в зазоре равна Ео. Затем половину зазора, как показано на рис. 2.13, заполнили однородным диэлектриком с проницаемостью е. Найти модули векторов Е и D в беих частях зазора (1 и 2), если при введении диэлектрика:
а) напряжение между обкладками не менялось;
б) заряды на обкладках оставались неизменными.



 Рис. 2.13
Рис. 2.13
Рис. 2.14
|
| Рис. 2.15 |
2.97. Решить предыдущую задачу с тем
отличием, что диэлектриком заполнили половину
зазора, как показано на рис. 2.14.
2.98. Половина пространства между обкладка
ми сферического конденсатора заполнена
(рис. 2.15) однородным диэлектриком с проница
емостью е. Заряд конденсатора q. Найти мо
дуль напряженности электрического поля между
обкладками как функцию расстояния г от
центра конденсатора.
2.99. Внутри шара из однородного диэлектрика с проницае
мостью е = 5,00 создано однородное электрическое поле напря
женности Е = 100 В/м. Радиус шара R = 3,0 см. Найти максималь
ную поверхностную плотность связанных зарядов и полный
связанный заряд одного знака.
2.100. Точечный заряд q находится в вакууме на расстоянии
/ от плоской поверхности однородного диэлектрика, заполняю
щего все полупространство. Проницаемость диэлектрика е.
Найти:
а) поверхностную плотность связанных зарядов как функцию
расстояния г от точечного заряда q;
б) суммарный заряд на поверхности диэлектрика.
2.101. Воспользовавшись условием и решением предыдущей
задачи, найти модуль силы, действующей на заряд q со
стороны связанных зарядов на поверхности диэлектрика.
Точечный заряд q находится на плоскости, отделяю щей вакуум от безграничного однородного изотропного диэлек трика с проницаемостью е. Найти модули векторов D и Е и потенциал ф как функции расстояния г от заряда q.
2.103. Небольшой проводящий шарик, имеющий заряд q,
находится в однородном изотропном диэлектрике с проницае
мостью е на расстоянии / от безграничной плоской границы,
отделяющей диэлектрик от вакуума. Найти поверхностную
плотность связанных зарядов на границе диэлектрик — вакуум
как функцию расстояния г от шарика. Исследовать полученный
результат при /-О.
2.104. Полупространство, заполненное однородным изотроп
ным диэлектриком с проницаемостью е, ограничено проводя
щей плоскостью. На расстоянии / от этой плоскости в
диэлектрике находится небольшой металлический шарик,
имеющий заряд q. Найти поверхностную плотность связанных
зарядов на границе с проводящей плоскостью как функцию
расстояния г от шарика.
| У////ЛТ |
2.105. Пластинка толщины h из однородного статически
поляризованного диэлектрика находится внутри плоского кон
денсатора, обкладки которого сое
динены между собой проводни
ком. Поляризованность диэлектри
ка равна Р (рис. 2.16). Расстояние
~~~ ' между обкладками конденсатора d.
Рис- 2Л6 Найти векторы Е и D внутри и
вне пластины.
2.106. Длинный диэлектрический цилиндр круглого сечения
поляризован так, что вектор Р = аг, где а - положительная
постоянная, г — расстояние от оси. Найти объемную плотность
р' связанных зарядов как функцию расстояния г от оси.
2.107. Диэлектрический шар поляризован однородно и
статически. Его поляризованность равна Р. Имея в виду, что
так поляризованный шар можно представить как результат
малого сдвига всех положительных зарядов диэлектрика
относительно всех отрицательных зарядов:
а) найти напряженность Е поля внутри шара;
б) показать, что поле вне шара является полем диполя и
потенциал поля ф = р0г/4л еог3, где р0 - электрический момент
шара, г - расстояние от его центра.
2.108. В однородное электрическое поле Ео поместили
однородный диэлектрический шар. При этих условиях диэлек-
трик поляризуется однородно. Найти напряженность Е поля внутри шара и поляризованность Р диэлектрика, проницаемость которого е. Воспользоваться результатом предыдущей задачи.
2.109. Два одинаковых небольших одноименно заряженных
шарика подвешены на изолирующих нитях равной длины к
одной точке. При заполнении окружающей среды керосином
угол расхождения нитей не изменился. Найти плотность
материала шариков.
2.110. На расстоянии г от точечного заряда q расположен
тонкий диск из диэлектрика с проницаемостью е. Объем диска
V, его ось проходит через заряд q. Считая, что радиус диска
значительно меньше г, оценить силу, действующую на диск.
23. Электроемкость. Энергия электрического поля
• Емкость плоского конденсатора:
C = ezaSld. (2.3а)
• Энергия взаимодействия системы точечных зарядов:
|l3 (2-36)
• Полная электрическая энергия системы с непрерывным распределением
заряда:
W*±fvpdV. (2.3в)
• Полная электрическая энергия двух заряженных тел:
W-Wl + W1*Wa, (2.3г)
где Wl и W2 — собственные энергии тел, Wn — энергия взаимодействия.
• Энергия заряжённого конденсатора:
W*qUp.=q2l2C = CU2l2. (2.3д)
• Плотность энергии электрического поля:
w = ED/2 = t€0£V2. (2.3e)
2.111. Найти емкость шарового проводника радиуса Rt = = 100 мм, окруженного прилегающим к нему концентрическим слоем диэлектрика проницаемости е = 6,0 и наружного радиуса #2 = 200 мм.
Ч-ьчэ
2.112. К напряжению U = 100 В подключили последовательно
два одинаковых конденсатора, каждый емкости С = 40 пф.
Затем один из них заполнили диэлектриком проницаемости
е = 3,0. Во сколько раз уменьшилась напряженность электричес
кого поля в этом конденсаторе? Какой заряд пройдет в цепи?
2.113. Пространство между обкладками плоского конденсато
ра заполнено последовательно двумя диэлектрическими слоями
1 я 2 толщины dx и dj и проницаемости гх и е2. Площадь
каждой обкладки равна S. Найти:
а) емкость конденсатора;
б) плотность а' связанных зарядов на границе раздела
слоев, если напряжение на конденсаторе равно U и электриче
ское поле направлено от слоя 1 к слою 2.
2.114. Зазор между обкладками плоского конденсатора
заполнен диэлектриком, проницаемость которого меняется в
перпендикулярном обкладкам направлении - растет линейно от
ej до е2. Площадь каждой обкладки S, расстояние между ними
d. Найти:
а) емкость конденсатора;
б) объемную плотность связанных зарядов как функцию е,
если заряд конденсатора q и поле Е в нем направлено в
сторону возрастания е.
2.115. Найти емкость сферического конденсатора, радиусы
обкладок которого а и Ъ, причем а<Ъ, если пространство между обкладками заполнено диэлектриком:
а) проницаемости с;
б) проницаемость которого зависит от расстояния г до
центра конденсатора как е = ос/г, где а - постоянная.
2.116. То же, что и в предыдущей задаче, но конденсатор
цилиндрический длины /ив пункте б) г - расстояние до оси
системы. Краевыми эффектами пренебречь.
2.117. Найти емкость сферического конденсатора, радиу
сы внутренней и внешней обкладок которого равны а и Ъ,
если пространство между обкладками заполнено наполовину
(см. рис. 2.15) однородным диэлектриком проницаемости е.
2.118. Два длинных прямых провода одинакового радиуса
сечения а расположены в воздухе параллельно друг другу.
Расстояние между их осями равно Ь. Найти взаимную емкость
проводов Cj на единицу их длины при условии а «Ь. Вычис
лить Cj, если а = 1,00 мм и Ь = 50мм.
2.119. Длинный прямой провод расположен параллельно
проводящей плоскости. Радиус сечения провода а, расстояние
между осью провода и проводящей плоскостью Ь. Найти взаимную емкость этой системы на единицу длины провода при
условии а «Ъ.
2.120. Найти взаимную емкость системы из двух одинаковых
металлических шариков радиуса а, расстояние между центрами
которых Ъ, причем а«Ъ. Система находится в однородном
диэлектрике проницаемости е.
2.121. Определить взаимную емкость системы, которая
состоит из металлического шарика радиуса а и проводящей
плоскости, отстоящей от центра шарика на расстояние /, при
условии а«1.
2.122. Найти емкость системы одинаковых конденсаторов
между точками А и В, которая показана:
а) на рис. 2.17;
| С |
б) на рис. 2.18.
| А | ii и | nJ | ||
| и с, | ifи Сг | В | ||
нн-и
С
В
Рис. 2.17
Рис. 2,18
2.123. Четыре одинаковые металлические пластины расположены в воздухе на расстоянии d = 1,00 мм друг от друга. Площадь каждой пластины S = 220 см2. Найти емкость системы между точками А и В, если пластины соединены так, как показано:
а) на рис. 2.19; б) на рис. 2.20.

 -о А
-о А
ОВ
-ой
Рис. 2.19
Рис. 2.20
2.124. Конденсатор емкости Cj = 1,0 мкФ выдерживает
напряжение не более Ul = 6,0кВ, а конденсатор емкости
Сг = 2,0 мкФ — не более иг = 4,0 кВ. Какое напряжение может
выдержать система их этих двух конденсаторов при последова
тельном соединении?
2.125. В схеме (рис. 2.21) найти разность потенциалов между
точками А и В, если ЭДС ^ = 110 В и отношение емкостей
Сг\Сх = Л =2,0.
I
с,
В
О
Т
ТсТс
Рис. 2.21
Рис. 2.22
2.126. Найти емкость бесконечной цепи, которая образована повторением одного и того же звена из двух одинаковых конденсаторов, каждый емкости С (рис. 2.22).
| в -о— |
| НИ с, |
| Рис. 2.23 |
| -ih |
| Рис. 2.24 |
2.127. В некоторой цепи имеется
участок АВ (рис. 2.23). ЭДС ^=10 В,
Cj = 1,0 мкФ, С2 = 2,0 мкФ и разность по
тенциалов <р^-фа=5,0 В. Найти напря
жение на каждом конденсаторе.
2.128. В схеме (рис. 2.24) найти
направление электрического поля в кон
денсаторах и напряжения на них, если
£?j = 10 В, ^ = 15 В, Cj = 4,0 мкФ и С2 =
= 6,0 мкФ.
2.129. Найти разность потенциалов
Фл - ц>в между точками А и В систе
мы, показанной:
а) на рис. 2.25; б) на рис. 2.26.

|
В

 с1
с1
Рис. 2.25
С,.
2.130. Конденсатор емкости Cj = 1,0mkO, заряженный до напряжения t/ = 110 В, подключили параллельно к концам системы из двух последовательно соединенных конденсаторов, емкости которых С2 = 2,0 мкФ и С3 = 3,ОмкФ. Какой заряд протечет при этом по соединительным проводам?
2.131. Какие заряды протекут
после замыкания ключа К в схеме
(рис. 2.27) через сечения 1 и 2 в
направлениях, указанных стрелками?
2.132. В схеме (рис. 2.28) % =
= 60 В, С] = 2,0мкФ и С2 = 3,0мкФ.
Найти заряды, которые протекут
после замыкания ключа К через
сечения 1 и 2 в направлениях, ука
занных стрелками.

|
Т
/г>
Рис. 2.27

|
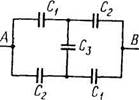
Рис. 2.29
2.133. Найти емкость схемы (рис. 2.29) между точками А
и В.
2.134. Три электрона, находившихся на расстоянии а =
= 10,0 мм друг от друга, начали симметрично разлетаться под
действием взаимного отталкивания. Найти их максимальные
скорости.
2.135. Определить суммарную энергию взаимодействия
точечных зарядов, расположенных в вершинах квадрата со
стороной а в системах, которые показаны на рис. 2.30.
Г
Я ЯГ
Ч IV
А 6 в
Рис. 2.30
2.136. Тонкий стержень длины I расположен по оси тонкого кольца радиуса R так, что один его конец совпадает с центром О кольца. Кольцо и стержень имеют заряды q0 n q, причем линейная плотность заряда на стержне изменяется вдоль него
линейно, начиная с нуля в точке О. Найти электрическую энергию взаимодействия кольца со стержнем.
2.137. Точечный заряд q находится на расстоянии / от
проводящей плоскости. Найти:
а) энергию взаимодействия этого заряда с зарядами,
индуцированными на плоскости;
б) собственную энергию зарядов на плоскости.
2.138. Плоский конденсатор, площадь каждой пластины
которого 5 = 200 см2 и расстояние между ними </ = 5,0мм, поместили во внешнее однородное электрическое поле с Е = 1,30 кВ/см, перпендикулярное пластинам. Затем пластины замкнули проводником, после, чего проводник убрали и конденсатор перевернули на 180° вокруг оси, перпендикулярной направлению поля. Найти совершенную при этом работу против электрических сил.
2.139. Конденсатор емкости Сх = 1,0 мкФ, заряженный до
напряжения 17 = 300 В, подключили параллельно к незаряженно
му конденсатору емкости С2 = 2,0 мкФ. Найти приращение
электрической энергии системы к моменту установления
равновесия. Объяснить полученный результат.
2.140. Сколько теплоты выделится при переключении ключа
К из положения / и 2 в цепи, показанной:
а) на рис. 2.31; б) на рис. 2.32.

|
| ,С И |

Рис. 2.32
2.141. Система состоит из двух концентрических тонких
металлических оболочек с радиусами /?1 и Щ и соответствую
щими зарядами qx и q2. Найти собственную энергаю Wt и W2
каждой оболочки, энергию взаимодействия Wn оболочек и
полную электрическую энергию W системы.
2.142. Заряд q распределен равномерно по объему шара
радиуса R. Считая проницаемость е = 1, найти:
а) собственную электрическую энергию шара;
б) отношение энергии Wx внутри шара к энергии W2 в окружающем пространстве.
2.143. Точечный заряд q = 3,0 мкКл находится в центре
шарового слоя из однородного диэлектрика проницаемости
е = 3,0. Внутренний радиус слоя а = 250 мм, внешний Ъ =
= 500 мм. Найти электрическую энергию в данном слое.
2.144. Найти энергию электрического поля точечного заряда
q в пустом полупространстве, которое ограничено плоскостью,
отстоящей на расстояние а от заряда.
2.145. Сферическую оболочку радиуса Яр равномерно за
ряженную зарядом q, расширили до радиуса Е^. Найти работу,
совершенную при этом электрическими силами.
2.146. В центре сферической оболочки, равномерно за
ряженной зарядом q = 5,0 мкКл, расположен точечный заряд
^0= 1,50 мкКл. Найти работу электрических сил при расшире
нии оболочки — увеличении ее радиуса от Rx = 50 мм до
#2= 100 мм.
2.147. Сферическая оболочка заряжена равномерно с повер
хностной плотностью а. Воспользовавшись законом сохранения
энергии, найти модуль электрической силы на единицу повер
хности оболочки.
2.148. Точечный заряд q находится в центре О сферическо
го незаряженного проводящего слоя с малым отверстием вдоль
радиуса. Внутренний и внешний радиусы слоя равны соответ
ственно а и Ь. Какую работу надо совершить против электри
ческих сил, чтобы медленно перенести заряд q из точки О на
бесконечность?
2.149. Имеется плоский воздушный конденсатор, площадь
каждой обкладки которого равна S. Какую работу против
электрических сил надо совершить, чтобы увеличить расстояние
между обкладками от хх до х2, если при этом поддерживать
неизменным:
а) заряд конденсатора q;
б) напряжение на конденсаторе U1
2.150. Внутри плоского конденсатора находится параллельная
обкладкам пластина, толщина которой составляет т| = 0,60
расстояния между обкладками. Емкость конденсатора в отсут
ствие пластины С = 20нФ. Конденсатор сначала подключили к
источнику постоянного напряжения 17 = 200 В, затем отключили
и после этого медленно извлекли пластину из зазора. Найти
работу, совершенную против электрических сил при извлечении
пластины, если она:
а) металлическая; б) стеклянная.
2.151. Плоский конденсатор, расстояние между пластинами
которого d = 1,0 мм, опустили в горизонтальном положении в
воду, которая целиком заполнила его. Затем конденсатор
подключили к постоянному напряжению 17 = 500 В. Найти
приращение давления воды в конденсаторе.
2.152. Плоский конденсатор расположен горизонтально так,
что одна его пластина находится над поверхностью жидкости,
другая - под ее поверхностью. Диэлектрическая проницаемость
жидкости е, ее плотность р. На какую высоту поднимется
уровень жидкости в конденсаторе после сообщения его пласти
нам заряда с поверхностной плотностью а?
2.153. В цилиндрический конденсатор вводят длинный
цилиндрический слой диэлектрика проницаемости е, заполняю
щий практически весь зазор между обкладками. Средний радиус
обкладок R, зазор между ними d, причем d«R. Обкладки конденсатора подключены к источнику постоянного напряжения U. Найти модуль электрической силы, втягивающей диэлектрик в конденсатор.

|
2.154. Конденсатор состоит из двух непод
вижных пластин, имеющих форму полукруга
радиуса R, и расположенной между ними
подвижной пластины из диэлектрика прони-
цаемости е, которая может свободно повора-
чиваться вокруг оси О (рис. 2.33). Толщина
подвижной пластины d, что практически
Рис. 2.33 равно расстоянию между неподвижными
пластинами. Конденсатор поддерживают при постоянном напряжении U. Найти модуль момента сил относительно оси О, действующих на подвижную пластину в положении, показанном на рисунке.
2.4. Электрический ток
• Закон Ома для неоднородного участка цепи:
I'UnIR = {Vl-V2^n)/R, (2.4а)
где Un — падение напряжения на данном участке.
* Закон Ома в дифференциальной форме:
j = o(E + E*), (2.46)
где Е* — напряженность поля сторонних сил.
Правила Кирхгофа:
• Мощность тока Р и тепловая мощность Q:
Р = ОТ = («, -», + «у /, <? - JU*. (2.4г)
• Удельная мощность тока Ри и удельная тепловая мощность тока Qn:
^-ЦЕ + Е*), <?„-рУ*. (24д)
• Плотность тока в металле:
(2.4e)
где п — средняя скорость носителей.
• Число ионов, рекомбинирующих за единицу времени в единице объема
(2.4ж)
где г - коэффициент рекомбинации.
| В |
| j | ||
2.155. Длинный равномерно заряженный по поверхности
цилиндр радиуса а = 1,0 см движется со скоростью v = 10 м/с
вдоль своей оси. Напряженность электрического поля непосред
ственно у поверхности цилиндра £ = 0,9кВ/см. Найти ток,
обусловленный механическим переносом заряда.
2.156. Воздушный цилиндрический конденсатор, подключен
ный к источнику напряжения 17 = 200 В, погружают в вертикаль
ном положении в сосуд с дистиллированной водой со скоростью
v= 5,0 мм/с. Зазор между обкладками конденсатора <2 = 2,0мм,
средний радиус обкладок г = 50 мм. Имея в виду, что d«r,
найти ток, текущий по проводящим проводам.
2.157. Найти сопротивление проволоч
ного каркаса, имеющего форму куба
(рис. 2.34), при включении его в цепь
между точками:
Дата добавления: 2015-08-02; просмотров: 1543 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Механика несжимаемой жидкости | | | А) 1-7; б) 1-2; в) 1-3. Сопротивление каждого ребра каркаса равно R. |