Упругие волны. Акустика 2 страница

3261. Найти с помощью уравнений (3.4 е) распределение
тока I(x,t) в двухпроводной линии, вдоль которой установилось
распределение напряжений по закону U= (7_mcos(itx)cos(<of),
если волновое сопротивление линии равно р.

3.262. Найти с помощью уравнений (3.4 е) закон распределе­ния амплитуд напряжений U_m(x) и токов 1_т(х) при наличии

собственных колебаний в двухпроводной линии длины I, у которой:

а) концы с обеих сторон размокнуты;

б) концы с обеих сторон замкнуты;

в) левые концы линии замкнуты, правые разомкнуты.
2263. Найти длину L воздушной двухпроводной линии,

концы которой замкнуты с обеих сторон, если резонанс в линии наступает при двух последовательных частотах Vj = 3,0 МГц и v₂ =4,5 МГц.

3264. Доказать, что у замкнутой системы заряженных нерелятивистских частиц с одинаковым удельным зарядом дипольное излучение отсутствует.

3.265. Найти среднюю мощность излучения электрона, совершающего гармонические колебания с амплитудой

а = 0,10 нм и частотой «= 6,5 • 10^м с"¹.

3266. Найти мощность излучения нерелятивистской частицы с зарядом е и массой /и, движущейся по круговой орбите радиуса R в поле неподвижного точечного заряда q.

3J267. Нерелятивистский протон влетел по нормали в полупространство с поперечным однородным магнитным полем, индукция которого В = 1,0 Тл. Найти отношение энергии, потерянной протоном на излучение за время движения в поле, к его первоначальной кинетической энергии.

3.268. Нерелятивистская заряженная частица движется в
поперечном однородном магнитном поле с индукцией В. Найти
закон убывания (за счет излучения) кинетической энергии
частицы во времени. Через сколько времени ее кинетическая
энергия уменьшается в е раз? Вычислить это время для
электрона и протона, если В = 1,0 Тл.

3.269. Заряженная частица движется вдоль оси у по закону
у =acos(At, а точка наблюдения Р находится на оси х на
расстоянии / от частицы (1>>а). Найти отношение плотностей
потока электромагнитного излучения 5,/5₂ в точке Р в момен­
ты, когда координата частицы у_х=0 и у_г = а. Вычислить это

отношение, если о =2,01 • 10⁸ см"¹ и /= 50,0 м. Запаздывание пренебрежимо мало.

3270. В направлении максимального излучения на расстоя­
нии г₀ = 10 м от элементарного диполя (волновая зона) амплиту­
да напряженности электрического поля Е_т = 6 В/м. Найти
среднее значение плотности потока энергии на расстоянии
г = 20 м от диполя в направлении, составляющем угол t = 30°
с его осью.

3271. Электромагнитная волна, излучаемая диполем,
распространяется в вакууме так, что в волновой зоне на луче.
перпендикулярном оси диполя, на расстоянии г от него
среднее значение плотности потока энергии равно S_o. Найти
среднюю мощность излучения диполя.

3272. Средняя мощность, излучаемая диполем, равна Р_о.
Найти среднюю плотность энергии электромагнитного поля в
вакууме в волновой зоне на луче, перпендикулярном оси

диполя, на расстоянии г от него.

3273. Постоянный по модулю электрический диполь с
моментом р вращают с угловой скоростью w вокруг оси,
перпендикулярной оси диполя и проходящей через его середи­
ну. Найти мощность излучения диполя.

3274. Считая, что частица имеет форму шарика и поглоща­
ет весь падающий на нее свет, найти радиус частицы, при
котором гравитационное притяжение ее к Солнцу будет
компенсироваться силой светового давления. Мощность

светового излучения Солнца /^>=4 10²⁶Вт, плотность частицы

р = 1,0 г/см³.

3275. В опыте Физо по определению скорости света расстоя­
ние между зубчатым колесом и зеркалом / = 7,0 км, число
зубцов z=720. Два последовательных исчезновения света
наблюдали при частотах вращения колеса n_t = 283 об/с и
п_г = 313 об/с. Найти скорость света.

3276. Источник света движется со скоростью v относительно
приемника. Показать, что при v«c относительное изменение
частоты света определяется формулой (3.4 и).

3277. Одна из спектральных линий, испускаемых возбужден­
ными ионами Не⁺, имеет длину волны А=410нм. Найти
доплеровское смещение А А. этой линии, если ее наблюдать под
углом Ь = 30° к пучку ионов, движущихся с кинетической
энергией К = 10 МэВ.

3278. При наблюдении спектральной линии А = 0,59 мкм в
направлениях на противоположные края солнечного диска на
его экваторе обнаружили различие в длинах волн на

б А = 8,0 пм. Найти период вращения Солнца вокруг собственной оси.

3279. Эффект Доплера позволил открыть двойные звезды
столь удаленные, что разрешение их с помощью телескопа
оказалось невозможным. Спектральные линии таких звезд
периодически становятся двойными, из чего можно заключить,
что источником являются две звезды, обращающиеся вокруг их
центра масс. Считая массы обеих звезд одинаковыми, найти
расстояние между ними и их массы, если максимальное

расщепление спектральных линий (ДА/А)_т = 1,2 -ИГ⁴, причем оно возникает через каждые т = 30 сут.

3280. Плоская электромагнитная волна частоты w₀ падает нормально на поверхность зеркала, движущегося навстречу с релятивистской скоростью и. Найти с помощью формулы Доплера частоту отраженной волны. Рассмотреть также случай

3281. Радиолокатор работает на длине волны А = 50,0 см.
Найти скорость приближающегося самолета, если частота
биений между сигналами передатчика и отраженными от
самолета в месте расположения локатора Av = 1,00 кГц.

3282. Имея в виду, что фаза электромагнитной волны
int-kx есть инвариант, т.е. не меняется при переходе от одной
инерциальной системы отсчета к другой, определить, как
преобразуются частота о и волновое число к.

3283. С какой скоростью удаляется от нас некоторая
туманность, если линия водорода А_о = 434 нм (для неподвижного
источника) в ее спектре смещена в длинноволновую сторону на
130 нм?

3284. С какой скоростью должна была бы двигаться
автомашина, чтобы красный свет светофора (А=0,70мкм)
превратился в зеленый (Я'=0,55 мкм)?

3285. По некоторой прямой движутся в одном направлении
наблюдатель со скоростью v_x = 0,50 с и впереди него источник
света со скоростью i>₂=0,75c. Собственная частота света равна
о₀. Найти частоту света, которую зафиксирует наблюдатель.

3286. Одна из спектральных линий атомарного водорода
имеет длину волны А = 656,3 нм. Найти доплеровское смещение
Д А этой линии, если ее наблюдать под прямым углом к пучку
атомов водорода с кинетической энергией К = 1,0 МэВ (попереч­
ный доплер-эффект).

3287. Источник, испускающий элек- „

тромагнитные сигналы с собственной --- 1--------»•

частотой v₀ = 3,0 ГГц, движется со ско- |

ростью v = 0,80 с по прямой, отстоящей |

от неподвижного наблюдателя Р на in

расстояние / (рис. 3.43). Найти частоту

Рис. 3.43

сигналов, принимаемых наблюдателем в момент:

а) когда источник окажется в точке О;

б) когда наблюдатель увидит его в точке О.

3.288. Узкий пучок элект­ронов проходит над поверх­ностью металлического зер­кала, на котором нанесена система штрихов с шагом d = 2,0 мкм. Электроны дви­жутся с релятивистской ско­ростью и перпендикулярно

_Рис 3 44 штрихам. При этом наблюда-

ется видимое излучение: тра­ектория электронов имеет вид полоски, окраска которой меняется в зависимости от угла наблюдения Ь (рис. 3.44). Объяснить это явление. Найти длину волны наблюдаемого излучения при Ь = 45°.

3289. Из-за движения Земли направление на звезду в плоскости эклиптики в течение года периодически меняется, и звезда совершает кажущиеся колебания в пределах угла а =41". Найти скорость Земли на орбите.

3.290. Найти угол полураствора конуса, в котором будут видны звезды, расположенные в полусфере для земного наблюдателя, если двигаться относительно Земли со скоростью, отличающейся от скорости света на ц = 1,0 %.

Часть 4

ОПТИКА

4.1. Фотометрия и геометрическая оптика

• Кривая относительной спектральной чувствительности глаза V(X) показана на рис. 4.1.

j

\

\

т

\

А = 1,6 мВт/л h для K=Q,555Ht

0,3

1

f

\

\

0,6

\

/

\

\

а*

\

\

...

/

\

0,2

/

\

/

и

t

у*

s

mm

mm

(Я

■•а

■ч.

Шш т

Q/tO 0,Ь5 0,50 0,55 0,60 0,65 0,70 К,тн

Рис. 4.1

• Сила света J и освещенность Е:

/ = 4Ф/</0, E=dQ^ldS. (4.1а)

• Освещенность, создаваемая точечным изотропным источником:

£ = (//r²)cosa, E = dQ_wldS, (4.16)

где a - угол между нормалью поверхности и направлением на источник.

• Светимость М и яркость L:

М-

dS dQtScostt

• Светимость для ламбертовского источника:

(4.1 в)

(4.1 г) 203

(4.1 Д) (4.1 е) (4.1 ж)

• Связь между преломляющим углом в призмы и углом а наименьшего

отклонения:

sin[(a+e)/2]=nsm(e/2),

где Л - показатель преломления вещества призмы.

• Формула сферического зеркала:

где R — радиус кривизны зеркала.

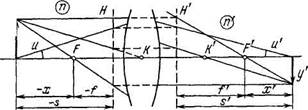
• Формулы центрированной оптической системы (рис. 4.2):

If

Рис. 4.2

• Соотношения между фокусными расстояниями и оптической силой:

/'=п'/Ф, /=-п/Ф, /7/=-п'/п. (4.1 з)

• Оптическая сила сферической преломляющей поверхности:

(4.1 и)

Оптическая сила тонкой линзы:

(4.1 к)

Рис. 4.3

где л и л₀ - показатели преломления вещества линзы и среды.

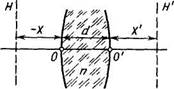
• Оптическая сила толстой линзы
толщины d:

Ф = Ф, + Ф₂ - (<*/л)Ф,Ф₂. (4.1л)

Эта формула справедлива и для системы из двух тонких линз, между которыми находится среда с показателем прелом­ления л.

• Главные плоскости Я и Я' отстоят

от вершин О и О' поверхностей толстой линзы (рис. 4.3) на расстояниях:

• Увеличение оптического прибора:

(4.1 м) (4.1 н)

где ф' и ф — угловые размеры предмета при наблюдении через прибор и без него (в случае лупы и микроскопа угол ф соответствует наблюдению на расстоянии наилучшего зрения Ц,=25 см.).

4.1. Найти с помощью кривой относительной спектральной чувствительности глаза (см.рис. 4.1):

а) поток энергии, соответствующий световому потоку 1,0 лм
и длиной волны 0,51 и 0,64 мкм;

б) световой поток, приходящийся на интервал длин волн от
0,58 до 0,63 мкм, если соответствующий поток энергии
Ф_э = 4,5 мВт, причем последний распределен равномерно по
всем длинам волн этого интервала. Считать, что в данном
спектральном интервале функция V(X) линейная.

42. Точечный изотропный источник испускает световой
поток Ф = 10 мл с длиной волны Я =0,59 мкм. Найти амплитуд­
ные значения напряженностей электрического и магнитного
полей этого светового потока на расстоянии г = 1,0 м от
источника. Воспользоваться рис. 4.1.

43. Найти световую энергию, которая падает на планету за
период ее обращения вокруг Солнца (по вытянутому эллипсу),
если световая мощность Солнца Р, площадь сечения планеты
S и в момент, когда планета находится на минимальном
расстоянии г₀ от Солнца, ее скорость равна v₀.

4.4. Определить среднюю освещенность облучаемой части
непрозрачной сферы, если на нее падает:

а) параллельный световой поток, создающий в точке
нормального падения освещенность Е_о;

б) свет от точечного изотропного источника, находящегося
на расстоянии / = 100 см от центра сферы; радиус сферы
Л = 60 см и сила света / = 36 кд.

4.5. Найти светимость поверхности, яркость которой зависит
от направления как L = L₀cost, где Ь — угол между направле­
нием излучения и нормалью к поверхности.

4.6. Некоторая светящаяся поверхность подчиняется закону
Ламберта. Ее яркость равна L. Найти:

а) световой поток, излучаемый элементом AS этой повер­
хности внутрь конуса, ось которого нормальна к данному
элементу, если угол полураствора конуса равен Ъ;

б) светимость такого источника.

4.7. Над центром круглого стола радиуса R = 1,0 м подвешен
небольшой светильник в виде плоского горизонтального диска
площади S = 100 см². Яркость светильника не зависит от

направления и равна L = 1,6 • 10⁴ кд/м². На какой высоте от поверхности стола надо поместить светильник, чтобы освещен-

ность периферийных точек стола была максимальной? Какова будет эта освещенность?

4.8. На высоте h = 1,0 м над центром круглого стола радиуса
R = 1,0 м подвешен точечный источник, сила света которого /
так зависит от направления, что освещенность всех точек стола
оказывается равномерной. Найти вид функции 1(Ь), где Ь -
угол между направлением излучения и вертикалью, а также
световой поток, падающий на стол, если / (0) = /₀ = 100 кд.

4.9. Вертикальный луч проектора освещает центр потолка
круглой комнаты радиуса R = 2,0 м. При этом на потолке
образуется небольшой зайчик площадью S = 100 см². Освещен­
ность зайчика Е = 1000 лк. Коэффициент отражения потолка
р =0,80. Найти наибольшую освещенность стены, создаваемую
светом, отраженным от потолка. Считать, что отражение
происходит по закону Ламберта.

4.10. Равномерно светящийся купол, имеющий вид полусфе­
ры, опирается на горизонтальную поверхность. Определить
освещенность в центре этой поверхности, если яркость купола
равна L и не зависит от направления.

4.11. Ламбертовский источник имеет вид бесконечной
плоскости. Его яркость равна L. Найти освещенность площад­
ки, расположенной параллельно данному источнику.

4.12. Над столом находится светильник - плоский горизон­
тальный диск радиуса R = 25 см. Расстояние от него до повер­
хности стола h = 75 см. Освещенность стола под центром
светильника Е_о = 70 лк. Найти светимость этого источника,
считая его ламбертовским.

4.13. Небольшой светильник, имеющий вид равномерно
светящейся сферы радиуса R - 6,0 см, находится на расстоянии

h = 3,0 м от пола. Яркость светильника L = 2,0 • 10⁴ кд/м² и не зависит от направления. Найти освещенность пола непосред­ственно под светильником.

4.14. Записать в векторном виде закон отражения светового
луча от зеркала — через направляющие орты е и е' падающе­
го и отраженного лучей и орт п внешней нормали к повер­
хности зеркала.

4.15. Показать, что луч света, последовательно отразившийся
от трех взаимно перпендикулярных плоских зеркал, изменит
свое направление на прямо противоположное.

4.16. При каком значении угла падения Ь₁ луч, отраженный
от поверхности воды, будет перпендикулярен преломленному
лучу?

4.17. Имеются две оптические среды с плоской границей
раздела. Пусть f>_lnp — предельный угол падения луча, a b_t —
угол падения, при котором преломленный луч перпендикулярен
отраженному (луч идет из оптически более плотной среды).
Найти относительный показатель преломления этих сред, если
sinftj^/sin©! = _ч = 1,28.

4.18. Луч света падает на плоскопараллельную стеклянную
пластину толщины d = 6,0 см. Угол падения Ь = 60°. Найти
смещение луча, прошедшего через эту пластину.

4.19. На краю бассейна стоит человек и наблюдает камень,
лежащий на дне. Глубина бассейна А, На каком расстоянии от
поверхности воды видно изображение камня, если луч зрения
составляет с нормалью к поверхности воды угол ft?

4.20. Показать, что в призме с малым преломляющим углом
6 луч отклоняется на угол а ~ (л -1) 6 независимо от угла
падения, если последний также мал.

421. Луч света проходит через призму с преломляющим

углом 6 и показателем преломления л. Пусть а - угол отклонения луча. Показать, что при симметричном ходе луча через призму:

а) угол а минимален;

б) связь между углами а и 8 определяется формулой (4.1 д).

422. Для некоторой стеклянной призмы угол наименьшего
отклонения луча равен преломляющему углу призмы. Найти
последний.

423. Найти пределы, в которых может меняться угол
отклонения луча при прохождении стеклянной призмы с
преломляющим углом 8 = 60°

Дата добавления: 2015-08-02