|
Читайте также: |
• Уравнение динамики твердого тела, вращающегося вокруг неподвижной
оси z:
где Nt — алгебраическая сумма моментов внешних сил относительно оси Z.
• Теорема Штейнера:
1 = 1с + таг. (1.56)
• Кинетическая энергия твердого тела, вращающегося вокруг неподвиж
ной оси:
* Работа внешних сил при повороте твердого тела вокруг неподвижной оси:
• Кинетическая энергия твердого тела при плоском движении:
* Связь между угловой скоростью **' прецессии гироскопа, его моментом импульса М, равным 1ш, и моментом N внешних сил:
[w'M]=N.
1272. Тонкий однородный стержень А В массы т = 1,0 кг движется поступательно с ускорением а = 2,0 м/с2 под действием сил F, и F2 (рис. 1.49). Расстояние Ь = 20см, сила F2 = 5,0H. Найти длину стержня.
1273. Однородный шар массы т = = 4,0 кг движется поступательно по поверхности стола под действием постоянной силы F, как показано на рис. 1.50. Угол а = 45°, коэффициент трения it = 0,20. Найти F и ускорение шара.
F'
| '//////У//////////////// Рис. 1.50 |
В
Рис. 1.49
1274. К точке с радиусом-вектором г, = a i приложена сила
F, = А\, а к точке с тг = Ь$ - сила F2 = Bi. Здесь i и j — орты
осей х и у, А и В — постоянные. Найти плечо равнодействующей силы относительно начала координат.
1275. Однородный кубик массы т = 2,5кг, длина ребра
которого I = 100 мм, перемещают вправо, действуя силой
F = ll H (рис. 1.51). Коэффициент трения it = 0,15. Найти:
а) плечо Ъ равнодействующей сил
нормального давления относительно
центра кубика;
б) при каком значении F кубик
будет скользить не опрокидываясь. ^^^^^^^^^^
1276. В начальном положении сере- ^77777777777777777777
дина горизонтального однородного Рис 151
стержня массы т и длины / находит
ся над упором А (рис. 1.52). Левый
конец стержня начали мед
ленно тянуть за нить. Какую /////л
работу надо совершить, что- ^ г, Л. W
бы стержень выскочил из- П 0
W/7/f
под упора В, если расстоя
ние между упорами А и В Рис- *-52
равно а и коэффициент
трения между стержнем и упорами к?
1277. Имеется тонкий однородный стержень массы т и
длины /. Найти его момент инерции относительно оси,
проходящей через:
а) его конец и перпендикулярной самому стержню;
б) его центр и составляющей угол а со стержнем.
Найти момент инерции тонкой однородной прямоу гольной пластинки относительно оси, проходящей через одну из вершин пластинки перпендикулярно ее плоскости, если стороны пластинки равны а и Ь, а ее масса т.
1279. Тонкая однородная пластинка массы т = 0,60 кг имеет
форму равнобедренного прямоугольного треугольника. Найти ее
момент инерции относительно оси, совпадающей с одним из
катетов, длина которого а = 200 мм
1280. Вычислить момент инерции:
а) медного однородного диска относительно его оси, если
толщина диска ft = 2,0 мм и радиус R = 100 мм;
б) однородного сплошного конуса относительно его оси,
если масса конуса т и радиус основания R.
1281. Найти момент инерции тонкого проволочного кольца
радиуса а и массы т относительно оси, совпадающей с его
диаметром.
1282. Показать, что для тонкой пластинки произвольной
формы имеется следующая связь между моментами инерции:
/j + f2 = /3, где ], 2, 3 — три взаимно перпендикулярные оси,
проходящие через одну точку, причем оси 1 и 2 лежат в
плоскости пластинки.
Используя эту связь, найти момент инерции тонкого круглого однородного диска радиуса R и массы т относительно оси, совпадающей с одним из его диаметров.
1283. Момент инерции тела относительно взаимно параллельных осей 1 и 2 равен /j = l,00 гм2 и /2 = 3,0 гм2. Оси 1 и 2 расположены на расстояниях хг ~ 100 м и д^ = 300 мм от центра масс С тела. Найти момент инерции этого тела относительно оси, проходящей через точку С и параллельной осям 1 и 2.
|
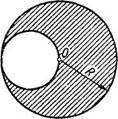
1284. Однородный диск радиуса R имеет круглый вырез (рис. 1.53). Масса оставшейся (заштрихованной) части диска равна т. Найти момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей:
а) через точку О;
б) через его центр масс.
| Рис. 1.53 |
1.285. Исходя из формулы для момента инерции однородного шара найти момент инерции тонкого сферического слоя массы т и радиуса R относительно оси, проходящей через его центр.
1286. На ступенчатый блок (рис. 1.54)
намотаны в противоположных направле
ниях две нити. На конец одной нити
действуют постоянной силой F, а к концу
другой нити прикреплен груз массы т.
Известны радиусы i?t и i^ блока и его
| F |
момент инерции / относительно оси вращения. Трения нет. Найти угловое ускорение блока.
| Рис. 1.54 |
1287. На однородный сплошной ци
линдр массы М и радиуса R плотно
намотана легкая нить, к концу которой прикреплен груз массы т (рис. 1.55). В момент г = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:
а) модуля угловой скорости цилиндра;
б) кинетической энергии всей системы.
| ТП\ |
| Рис. 1.55 |
1288. Концы тонких нитей, плотно намотанных на ось радиуса г диска Максвелла, прикреплены к горизонтальной штанге. Когда диск
раскручивается, штангу поднимают так, что диск остается неизменно на одной и той же высоте. Масса диска с осью т, их момент инерции относительно их оси симметрии /. Найти ускорение штанги.
1289. Горизонтальный тонкий однородный стержень А В
массы m и длины I может свободно вращаться вокруг
вертикальной оси, проходящей через его конец А. В некоторый
момент на конец В начала действовать постоянная сила F,
которая все время перпендикулярна первоначальному положе
нию покоившегося стержня и направлена в горизонтальной
плоскости. Найти угловую скорость стержня как функцию его
угла поворота ср из начального положения.
1290. Горизонтально расположенный тонкий однородный
стержень массы т подвешен за концы на двух вертикальных
нитях. Найти силу натяжения одной из нитей сразу после
пережигания другой нити.
1.291. Тонкий однородный стержень массы т = 0,50 кг и
длины I = 100 см может вращаться в вертикальной плоскости
вокруг оси, проходящей через сам стержень. Момент инерции
стержня относительно оси вращения 7 = 0,115 кгм2. Стержень установили в горизонтальном положении и отпустили. После этого он пришел в движение и остановился в вертикальном положении. Найти модуль тормозящего момента сил в оси, считая его постоянным.
|
1.292. В установке (рис. 1.56) известны
масса т однородного сплошного цилиндра,
его радиус R и массы тел т, и тг. Сколь
жения нити и трения в оси цилиндра нет.
Найти угловое ускорение цилиндра и отно
шение сил натяжения FJF2 вертикальных
участков нити в процессе движения. Убе
диться, что F1 = F1 при т-0.
| Рис. 1.56 |
1293. В установке (рис. 1.57) известны массы тел т1 и т2, коэффициент трения к между телом т, и горизонтальной поверхностью, а также масса блока т, который можно считать однородным диском. Скольжения нити по блоку нет. В момент t = 0 тело т2 начинает опускаться. Пренебрегая трением в оси блока, найти:
а) ускорение тела тг;
| /17, |
| \m? |
| Рис. 1.57 |
б) работу силы трения, действующей на тело mt, за первые l секунд после начала движения. 1294. Однородный стержень массы т падает с пренебрежимо малой начальной скоростью из вертикального положения, поворачиваясь вокруг неподвижной оси О, проходящей через его нижний конец. Найти горизонтальную и
вертикальную составляющие силы, с которой ось О действует на стержень в горизонтальном положении. Трения нет.
|
| Рис. 1.58 |
|
1295. Однородный сплошной цилиндр
радиуса R раскрутили вокруг его оси до
угловой скорости w0 и затем поместили в
угол (рис. 1.58). Коэффициент трения между
цилиндром и стенками равен к. Сколько
времени цилиндр будет вращаться в этом
положении?
1296. Б системе (рис. L.59) однородному
диску сообщили угловую скорость вокруг
горизонтальной оси О, а затем осторожно
опустили на него конец А стержня А В так,
что он образовал угол Ь=45" с вертикалью.
Трение имеется только между диском и
стержнем, коэффициент трения к = 0,13.
Пусть nJ и пг — числа оборотов диска до
остановки при его вращении по часовой
стрелки и против при одинаковой началь
ной скорости. Найти отношение Hj/rtj.
1.297. Однородный диск радиуса R раскрутили до угловой скорости о и осторожно положили на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен к?
| Рис. 1.59 |
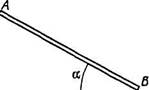
1298. Тонкий стержень А В массы т = = 50 г лежит на горизонтальной плоскости с коэффициентом трения £ = 0,12. Стержень может вращаться вокруг гладкой вертикальной оси, проходящей через его конец А. По концу В произвели кратковременный удар в горизонтальном направлении перпендикулярно стержню.
Импульс силы удара J- 0,50 Не. Сколько времени стержень будет вращаться'.'
1249. Маховик с начальной угловой скоростью «0 начинает тормозиться силами, момент которых относительно его оси пропорционален квадратному корню из его угловой скорости. Найти среднюю угловую скорость маховика за все время
торможения.
|
1Л(Н(. Однородный сплошной цилиндр р.пиуоа к и массы М может свободно вращаться s-пкрчт неподвижной юрнзонталышй оси О (риг. S.sVj), На цилиндр в один ряд намотан тонкий шнур длины.' и массы от Найги угловое ускорение цилиндра и зависимости oi длины х свешивающейся части шпури Счит;.>гь, -по центр масс намотанной части шнура uiixojxiin.ii на оси цилиндра
| Рис. 1.60 |
1301. Однородный СГСр1*УЛи> ДЛИНЫ / МОЖСТ
npai,,i!i,cH BOKf-vi горизонтальной оси. 1крменди-
KVJU'Mioii LlcfVivibO И ПрОХОДЯЩСЙ HCpCj 1)ДПН И'З
|
сг!. копии» (jHii J.61';. Систему равномср1н> вг),нца-ii)T с ^'лоиой CKOjitii.-.TLK) w иокруг вер шкальной оси. Найти \!uj; Ь.
| Рис. Ш |
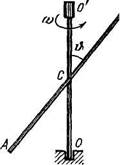
JJ02. Горизонгально расположенный однородный стержень л В массы m -1.40 ю. и длины /р=100 см вращается свободно вокруг иенодья/киой вертикальной оси ОСУ. проходящей через его конец А. Точка А находится ггосерединс оси ОСУ, дцина к(>т(>рой I = 55 см. При каком значении угловой (коросги стержня горизонтальная составляющая силы, действующей на нижний конец оси ОС, fiyuc't равна нулю? Какова при этом горизонтальная составляющая силы, действующей на верхний конец оси?
1305. Середина однородного стержня массы т и длины / же< тко соединена с вертикальной осью ОСУ так, что угол между стержнем и осью равен 0 (рис. 1.62). Концы оси ОО' укреплены в подшипниках. Система вращения без трения с угловой скоростью w. Найти:
а) модуль момента импульса стержня относительно точки
С и момент импульса относительно оси вращения;
б) модуль момента внешних сил, действующих на ось ОО'
при вращении.
|
1304. Гладкий однородный стержень
^В А В массы М и длины / свободно враща
ется с угловой скоростью «0 в горизон
тальной плоскости вокруг неподвижной
вертикальной оси, проходящей через его
конец А. Из точки А начинает скользить
по стержню небольшая муфта массы т.
Найти скорость v' муфты относительно
стержня в тот момент, когда она достигнет
его конца В.
| Рис. 1.62 |
1305. Однородная тонкая квадратная
пластинка со стороной / и массы М
может свободно вращаться вокруг непод
вижной вертикальной оси, совпадающей с
одной из ее сторон. В центр пластинки по нормали к ней упруго ударяется шарик массы т со скоростью v. Найти:
а) скорость шарика v' сразу после удара;
б) горизонтальную составляющую результирующей силы, с
которой ось действует на пластинку после удара.
1306. Вертикально расположенный однородный стержень
массы М и длины / может вращаться вокруг своего верхнего
конца. В нижний конец стержня попала, застряв, горизонтально
летевшая пуля массы т, в результате чего стержень отклонил
ся на угол а. Считая т «М, найти:
а) скорость летевшей пули;
б) приращение импульса системы "пуля — стержень" за
время удара; какова причина изменения этого импульса;
в) на какое расстояние х от верхнего конца стержня
должна попасть пуля, чтобы импульс системы не изменился
в процессе удара.
1307. Горизонтально расположенный однородный диск
массы М и радиуса R свободно вращается вокруг вертикальной
оси, проходящей через его центр. Диск имеет радиальную
направляющую, вдоль которой может скользить без трения
небольшое тело массы т. К телу привязана нить, пропущен
ная через полую ось диска вниз. Первоначально тело находи
лось на краю диска и вся система вращалась с угловой
скоростью «0. Затем к нижнему концу нити приложили силу
F, с помощью которой тело медленно подтянули к оси вращения. Найти:
а) угловую скорость системы в конечном состоянии:
б) работу, которую совершила сила F.
1308. Человек массы mt стоит на краю горизонтального
однородного диска массы тг и радиуса R, который может
свободно вращаться вокруг неподвижной вертикальной оси,
проходящей через его центр. В некоторый момент человек
начал двигаться по краю диска, совершил перемещение на
угол ср' относительно диска и остановился. Пренебрегая
размерами человека, найти угол, на который повернулся диск
к моменту остановки человека.
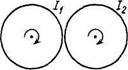
1309. Два горизонтальных диска свободно вращаются вокруг
вертикальной оси, проходящей через их центры. Моменты
инерции дисков относительно этой оси 1Х и /2, угловые
скорости «j и «2. После падения верхнего диска на нижний
оба диска из-за трения между ними начали через некоторое
время вращаться как единое целое. Найти:
а) установившуюся угловую скорость вращения дисков;
б) работу, которую совершили при этом силы трения.
|
1310. Двум одинакового радиуса дис
кам сообщили одну и ту же угловую
скорость <■>„ (рис. 1.63), а затем их
привели в соприкосновение, и система
через некоторое время пришла в новое
установившееся состояние движения.
Оси дисков неподвижны, трения в осях
нет. Моменты инерции дисков относи- Рис. 1.63
тельно их осей вращения равны 1Х и /2. Найти:
а) приращение момента импульса системы;
б) убыль ее механической энергии.
1311. Диск радиуса а может свободно вращаться вокруг
своей оси, относительно которой его момент инерции равен /0.
В момент г = 0 диск начали облучать по нормали к его
поверхности равномерным потоком частиц - N частиц в
единицу времени. Каждая частица имеет массу т и собствен
ный момент импульса М, направление которого совпадает с
направлением движения частиц. Считая, что все частицы
застревают в диске, найти его угловую скорость как функцию
времени o(t), если о(0) = 0. Изобразить примерный график
зависимости u>(f).
1312. Однородный диск радиуса R и массы т лежит на
гладкой горизонтальной поверхности. На боковую поверхность
диска плотно намотана нить, к свободному концу К которой
приложили постоянную горизонтальную силу F. После начала
движения диска точка К переместилась на расстояние L Найти угловую скорость диска к этому моменту.
|
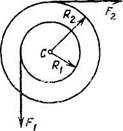
1313. Двухступенчатый блок радиусов
Rt и /L, положили на гладкую горизон
тальную поверхность. На ступени блока
плотно намотаны нити, к концам кото
рых приложили постоянные, взаимно
перпендикулярные силы F, и F,
(рис, 1.64, вид сверху). Сколько оборо
тов совершит блок за время, в течение
которого его ось С переместится на
расстояние /? Масса данного блока т,
Рис. 1.64 его момент инерции относительно оси С
равен /.
1314. Однородный диск радиуса # = 5,0см, вращающийся
вокруг своей оси с угловой скоростью w = 60 рад/с, падает в
вертикальном положении на горизонтальную шероховатую
поверхность и отскакивает под углом Ь = 30° к вертикали, уже
не вращаясь. Найти скорость диска сразу после отскакивания.
1315. Однородный шар скатывается без скольжения по
наклонной плоскости, составляющей угол а с горизонтом.
Найти ускорение центра шара и значение коэффициента
трения, при котором скольжения не будет.
1316. Однородный шар массы т = 5,0 кг скатывается без
скольжения по наклонной плоскости, составляющей угол
а = 30е с горизонтом. Найти кинетическую энергию шара через
t = 1,6 с после начала движения.
1317. Однородный стержень длины / = 110 см расположен
под углом а = 60° к гладкой горизонтальной поверхности, на
которую он опирается своим нижним концом. Стержень без
толчка отпустили. Найти скорость верхнего конца стержня
непосредственно перед падением его на поверхность,
1318. Катушка, момент инерции которой относительно ее
оси равен /, скатывается без скольжения по наклонной
плоскости. Пройдя от начала движения путь s, она приобрела
угловую скорость w. Найти силу трения покоя, считая ее
одинаковой на всем пути.
1319. Шарик А скатывается без скольжения с горки высоты
Н = 50 см, имеющей трамплин высоты h ■■- 15 см (рис. 1.65). С
какой скоростью шарик упадет на горизонтальную повер
хность?
|
| l_ |
|
у/////.
Рис. 1.65
Рис. 1.66
1320. Однородный цилиндр массы т = 8,0 кг и радиуса
R = 1,3 см (рис. 1.66) в момент Г = 0 начинает опускаться под
действием силы тяжести. Найти:
а) угловое ускорение цилиндра;
б) зависимость от времени мгновенной мощности, которую
развивает сила тяжести.
| т |
| ft |
| Рис, 1.67 |
|
1321. 
Нити намотаны на концах однородного сплошного
цилиндра массы от. Свободные концы нитей прикреплены к
потолку кабины лифта. Кабина начала подниматься с ускорени
ем а„. Найти ускорение а' цилиндра относительно кабины и
силу F, с которой цилиндр действует (через нити) на потолок.
1322. На гладкой наклонной плос
кости, составляющей угол а = 30° с
горизонтом, находится катушка с ни
ткой, свободный конец которой укреп
лен (рис. 1.67). Масса данной катушки
от = 200 г, се момент инерции относи
тельно собственной оси 7 = 0,45 г м2,
радиус намотанного слоя ниток г = 3,0 см.
Найти ускорение оси катушки.
1323. Однородный сплошной ци
линдр массы т лежит на двух горизон
тальных брусьях. На цилиндр намотана
нить, за свешивающийся конец которой
тянут с постоянной, вертикально направлен
ной силой F (рис. 1.68). Найти значения
силы F, при которых цилиндр будет катить
ся без скольжения, если коэффициент тре
ния равен к.
1324. На горизонтальной шероховатой
плоскости лежит катушка ниток массы т. Рис 16g
| F |
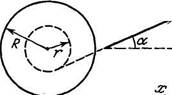Ее момент инерции относительно собственной оси I=ymR2, где у - числовой коэффициент, R — внешний радиус катушки. Радиус намотанного слоя
| '//////////////////////////У/////, |
| Рис. 1.69 |
ниток равен г. Катушку без скольжения начали тянуть за нить с постоянной силой F, направленной под углом а к горизонту (рис. 1.69). Найти:
а) проекцию на ось х ускорения оси катушки;
б) работу силы F за первые Г секунд движения.
1325. Система (рис. 1.70) состоит из двух одинаковых
однородных цилиндров, на которые симметрично намотаны две
легкие нити. Найти ускорение оси нижнего цилиндра в
процессе движения.
1326. В системе (рис. 1.71) известны масса т груза А,
масса М ступенчатого блока В, момент инерции / последнего
относительно его оси и радиусы ступеней блока R и 2R.
Найти ускорение груза А.
|
|
| А |
Рис. 1.70
У//////.
Рис. 1.72
1327. Сплошной однородный цилиндр А массы т1 может свободно вращаться вокруг горизонтальной оси, которая укреплена на подставке В массы тг (рис. 1.72). На цилиндр плотно намотана нить, к концу К которой приложили постоянную горизонтальную силу F. Трения между подставкой и плоскостью нет. Найти:
а) ускорение точки К;
б) кинетическую энергию этой системы через t секунд
после начала движения.
1328. На гладкой горизонтальной плоскости лежит доска
массы от, и на ней однородный шар массы тг. К доске
приложили постоянную горизонтальную силу F. С какими
ускорениями будут двигаться доска и центр шара в отсутствие
скольжения между ними?
1329. Сплошному однородному цилиндру массы т и
радиуса R сообщили вращение вокруг его оси с угловой
скоростью ы0, затем его положили боковой поверхностью на
горизонтальную плоскость и предоставили самому себе.
Коэффициент трения равен к. Найти:
а) время, в течение которого движение цилиндра будет
происходить со скольжением;
б) полную работу силы трения скольжения.
|
| Y777777777777777/77/77777/ |
1330. Однородный шар радиуса г скатывается без скольже
ния с вершины сферы радиуса R. Найти угловую скорость
шара после отрыва от сферы. Начальная скорость шара
пренебрежимо мала.
1331. Сплошной однородный цилиндр радиуса R катится по
горизонтальной плоскости, которая переходит в наклонную
плоскость, составляющую угол а с горизонтом (под уклон).
Найти максимальное значение скорости i>0 цилиндра, при
котором он перейдет на наклонную плоскость еще без скачка.
Скольжения нет.
1332. Однородный шар массы
т = 5,0 кг и радиуса R = 5,0 см ка
тится без скольжения по горизон
тальной поверхности. Вследствие
деформации в месте соприкоснове
ния шара и плоскости на шар при
движении вправо действует равно
действующая F сил реакции
(рис. 1.73). Найти модуль момента
силы F относительно центра О
шара, если шар, имевший в некото- Рис г 73
рый момент скорость и = 1,00 м/с,
прошел после этого до остановки путь s = 2,5 м. Момент силы
F считать постоянным.
1333. На гладкой горизонтальной поверхности лежит
однородный стержень массы т = 5,0кг и длины / = 90см. По
одному из концов стержня в горизонтальном направлении
перпендикулярно стержню произвели удар, импульс силы
которого J = 3,0 Не. Найти силу, с которой одна половина
стержня будет действовать на другую в процессе движения.
1334. Используя условие предыдущей задачи, найти:
а) на какое расстояние переместится центр стержня за
время его полного оборота;
б) кинетическую энергию стержня после удара.
1335. На гладкой горизонтальной поверхности лежит
однородный стержень массы т и длины /. На один из его
концов начали действовать постоянной, направленной все
время вертикально вверх силой F = mg. Найти угловую скорость
стержня в зависимости от угла <р его поворота.
1336. Однородный стержень
|
АВ длины 11 установили вертикально в углу, образованном гладкими плоскостями. В некоторый момент стержню сообщили пренебрежимо малую угловую скорость, и он начал падать, скользя по плоскостям, как пока-
W////////////////////////A а) угловую скорость ы и
Рис 174 угловое ускорение р стержня как
функции угла а - до момента отрыва точки А от плоскости;
б) при каком значении угла а стержень оторвется от вертикальной стенки?
1337. Однородный стержень длины I, укрепленный одним
концом в шарнире, отвели на угол Ь от вертикали и сообщи
ли его нижнему концу скорость v0 перпендикулярно вертикаль
ной плоскости, проходящей через стержень. При каком
минимальном значении v0 стержень при дальнейшем движе
нии пройдет через горизонтальное положение?
1338. На гладкой плоскости лежат небольшая шайба и
тонкий однородный стержень длины /, масса которого в ц раз
больше массы шайбы. Шайбе сообщили скорость v в горизон
тальном направлении перпендикулярно стержню, после чего
она испытала упругое соударение с концом стержня. Найти
скорость vc центра стержня после столкновения. При каком
значении ц скорость шайбы после столкновения будет равна
нулю? изменит направление на противоположное?
1339. Однородный стержень, падавший в горизонтальном
положении с высоты А, упруго ударился одним концом о край
массивной плиты. Найти скорость центра стержня сразу после
удара.
зано на рис. 1.74. Найти:
1340. Волчок массы m = 0,50 кг, ось которого наклонена под углом Ь - 30е к вертикали, прецессирует под действием силы тяжести. Момент инерции волчка относительно его оси
симметрии 7 = 2,0 гм2, угловая скорость вращения вокруг этой оси «= 350 рад/с, расстояние от точки опоры до центра масс волчка / = 10 см. Найти:
а) угловую скорость прецессии волчка;
б) модуль и направление горизонтальной составляющей
силы реакции, действующей на волчок в точке опоры.
|
|
1.341. На полу кабины лифта, кото
рая начинает подниматься с постоян
ным ускорением- а = 2,0 м/с2, установ
лен гироскоп - однородный диск
радиуса R = 5,0 см на конце стержня
длины I - 10 см (рис. 1.75). Другой
конец стержня укреплен в шарнире
О. Гироскоп прецессирует с частотой
л = 0.5 об/с. Пренебрегая трением и Рис. 1.75
массой стержня, найти собственную угловую скорость диска.
1342. Волчок, масса которого m = 1,0 кг и момент инерции
относительно собственной оси / = 4,0 г м2, вращается с
«= 320 рад/с, Его точка опоры находится на подставке, которую
перемещают в горизонтальном направлении с ускорением
а = 3,0 м/с2. Расстояние между точкой опоры и центром масс волчка / = 10 см. Найти модуль и направление вектора <■>' — угловой скорости прецессии волчка.
1343. Однородный шар массы т = 5,0 кг и радиуса
R = 6,0 см вращается с «= 1250 рад/с вокруг горизонтальной оси,
проходящей через его центр и укрепленной в подшипниках
подставки. Расстояние между подшипниками / = 15 см. Подстав
ку поворачивают вокруг вертикальной оси с «' = 5,0 рад/с.
Найти модуль и направление гироскопических сил.
1344. Диск массы т = 5,0 кг и радиуса R = 5,0 см вращается
с «= 330 рад/с. Расстояние между подшипниками, в которых
укреплена ось диска, / = 15 см. Ось вынуждают совершать
гармонические колебания вокруг горизонтальной оси с перио
дом Г=1,0с и амплитудой <ри = 20°. Найти максимальное
значение гироскопических сил, декйствующих на подшипники
со стороны оси диска.
1345. Корабль движется со скоростью v = 36 км/ч по дуге
окружности радиуса Я = 200 м. Найти момент гироскопических
сил, действующих на подшипники со стороны вала с махови
ком, которые имеют момент инерции относительно оси
вращения / = 3,8 103 кгм2 и делают л = 300 об/мин. Ось вращения расположена вдоль корабля.
1346. Локомотив приводится в движение турбиной, ось
которой параллельна осям колес. Направление вращения тур
бины совпадает с направлением вращения колес. Момент инер
ции ротора турбины относительно собственной оси 1=240 кгм2.
Найти добавочную силу давления на рельсы, обусловленную
гироскопическими силами, когда локомотив идет по закругле
нию радиуса Я = 250 м со скоростью v =50 км/ч. Расстояние
между рельсами / = 1,5 м. Турбина делает и = 1500 об/мин.
1.6. Упругие деформации твердого тела
• Закон Гука:
£ = а/Е, (1.6а)
где е — относительное удлинение, а - напряжение, Е — модуль Юнга.
• Связь между относительным поперечным сжатием (растяжением) е' и
относительным продольным растяжением (сжатием) е:
t' = -\it, (1.66)
где ц — коэффициент Пуассона.
• Связь между относительным сдвигом Y и тангенциальным напряже
нием т:
Y = f/G, (1.6b)
где G — модуль сдвига.
• Коэффициент сжимаемости (модуль всестороннего сжатия):
• Объемная плотность энергии упругой деформации:
1347. Какое давление необходимо приложить к торцам стального цилиндра, чтобы длина его не изменилась при повышении температуры на 100°С?
1.348. Какое давление изнутри (при отсутствии наружного давления) могут выдержать:
а) стеклянная трубка; б) стеклянная сферическая колба, у которых радиус г = 25 мм и толщина стенок Дг = 1,0 мм?
1349. Горизонтально расположенный медный стержень
длины / = 1,0 м вращают вокруг вертикальной оси, проходящей
через его середину. При какой частоте вращения он может
разорваться?
1350. Кольцо радиуса г = 25 см, сделанное из свинцовой
проволоки, вращают вокруг неподвижной вертикальной оси,
проходящей через его центр и перпендикулярной плоскости
кольца. При какой частоте вращения данное кольцо может
разорваться?
1351. Стальная проволока диаметра d = 1,0 мм натянута в
горизонтальном положении между двумя зажимами, находящи
мися на расстоянии / = 2,0 м друг от друга. К середине
проволоки - точке О - подвесили груз массы т = 0,25 кг. На
сколько сантиметров опустится точка О?
1352. Однородный упругий брусок движется по гладкой
горизонтальной плоскости под действием постоянной силы Fo,
равномерно распределенной по торцу. Площадь торца S,
модуль Юнга материала Е. Найти относительное сжатие бруска
в направлении действия данной силы.
1353. Тонкий однородный медный стержень длины I и
массы т равномерно вращается с угловой скоростью <о в
горизонтальной плоскости вокруг вертикальной оси, проходящей
через один из его концов. Найти силу натяжения в стержне в
зависимости от расстояния г до оси вращения, а также
удлинение стержня.
1354. Сплошной медный цилиндр длины I = 65 см поставили
на горизонтальную поверхность и сверху приложили вертикаль
ную сжимающую силу F = 1000H, которая равномерно распре
делена по его торцу. На сколько кубических миллиметров
изменился объем цилиндра?
1355. Медный стержень длины I подвесили за один конец
к потолку. Найти:
а) удлинение стержня под действием собственного веса;
б) относительное приращение его объема AV/V.
1356. Брусок из материала с модулем Юнга Е и коэффици
ентом Пуассона ц подвергли всестороннему сжатию давлением
р. Найти:
а) относительное уменьшение его объема;
б) связь между коэффициентом сжимаемости р и упругими
постоянными Е и |i.
65
Показать, что коэффициент Пуассона ц не может превышать 1/2.
1357. Установить связь между крутящим моментом N и углом закручивания <р для:
а) трубы, у которой толщина стенок Дг значительно
меньше радиуса трубы;
б) сплошного стержня круглого сечения.
Их длина /, радиус г и модуль сдвига G известны.
135$. Вычислить момент сил N, которые вызывают закручивание стальной трубы длины I = 3,0 м на угол <р = 2,0° вокруг ее оси, если внутренний и внешний диаметры трубы равны </j = 30mm и ^2 = 5Омм.
1359. Найти наибольшую мощность, которую можно
передать с помощью стального вала, вращающегося вокруг
своей оси с угловой скоростью ы = 120 рад/с, если его длина
/ = 200 см, радиус г = 1,50 см и допустимый угол закручивания
<р = 2,5°.
1360. Однордное кольцо массы т, имеющее внешний
радиус г2, плотно насажено на вал радиуса г1. Вал вращают
с постоянным угловым ускорением Р вокруг его оси. Найти момент упругих сил деформации сдвига в кольце в зависимости от расстояния г до оси вращения.
1361. Найти энергию упругой деформации стального стержня
массы т=3,1 кг, который растянут так, что его относительное
удлинение е = 1,0 • 10~3.
1362. Стальной цилиндрический стержень длины / и
радиуса г подвесили одним концом к потолку.
а) Найти энергию U упругой деформации стержня.
б) Выразить U через относительное удлинение стержня
Al/l.
1363. Какую работу необходимо совершить, чтобы стальную
полосу длины 1 = 2,0 м, ширины А = 6,0 см и толщины 5 = 2,0 мм согнуть в круглый обруч? Процесс происходит в пределах упругой деформации.
1364. Найти энергию упругой деформации стального
стержня, у которого один конец закреплен, а другой закручен
на угол <р = 6,0°. Длина стержня / = 1,0 м, его радиус г = 10 мм.
1365. Найти распределение плотности энергии упругой
деформации в стальном стержне в зависимости от расстояния
г до его оси. Длина стержня I, угол закручивания <р.
1366. Определить плотность энергии упругой деформации в
пресной воде на глубине А = 1000 м.
Дата добавления: 2015-08-02; просмотров: 1380 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ffl, ffU | | | Механика несжимаемой жидкости |