Читайте также:
|
| Рис. 2.34 |
2.158. При каком сопротивлении Rx в
цепочке (рис. 2.35) сопротивление между
точками А и В не зависит от числа
ячеек?
ZR 2R 2R 2R
4°~r4ZZD-r-{ZZr-r—-CZZHHZZr-п
JOGiZO
Рис. 2.35
| Rf |
| Rf |
|
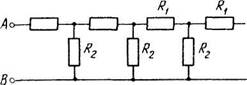
2.159. На рис. 2.36 показана бесконечная цепь, образованная повторением одного и того же звена - сопротивлений Rx = = 4,0 Ом и ^ = 3,0 Ом. Найти сопротивление между точками А и В.
Рис. 2.36
2.160. Имеется безграничная прово
лочная сетка с квадратными ячейками
(рис. 2.37). Сопротивление каждого
проводника между соседними узлами
равно jRq. Найти сопротивление R
этой сетки между точками А и В.
Указание. Воспользоваться принципами симметрии и суперпозиции.
| Рис. 2.37 |
2.161. Однородная слабо проводя
щая среда с удельным сопротивлени
ем р заполняет пространство между двумя коаксиальными
идеально проводящими тонкими цилиндрами. Радиусы цилин
дров а и Ь, причем а<Ъ, длина каждого цилиндра /. Прене
брегая краевыми эффектами, найти сопротивление среды между
цилиндрами.
2.162. Металлический шар радиуса а окружен концентрической тонкой металлической оболочкой радиуса Ь. Пространство между этими электродами заполнено однородной слабо проводящей средой с удельным сопротивлением р. Найти сопротивление межэлектродного промежутка. Рассмотреть также случай Ь-*оо.
2.163. Пространство между двумя проводящими концентри
ческими сферами, радиусы которых а и b (a<b), заполнено
однородной слабо проводящей средой. Емкость такой системы
равна С. Найти удельное сопротивление среды, если разность
потенциалов между сферами, отключенными от внешнего
напряжения, уменьшается в г\ раз за время Д*.
2.164. Два металлических шарика одинакового радиуса а
находятся в однородной слабо проводящей среде с удельным
сопротивлением р. Найти сопротивление среды между шарика
ми при условии, что расстояние между ними значительно
больше а.
2.165. Металлический шарик радиуса а находится на
расстоянии / от безграничной идеально проводящей плоскости.
Пространство вокруг шарика заполнено однородной слабо
проводящей средой с удельным сопротивлением р. Найти для
случая а«1:
а) плотность тока у проводящей плоскости как функцию
расстояния г от шарика, если разность потенциалов между
шариком и плоскостью равна U;
б) сопротивление среды между шариком и плоскостью.
2.166. Два длинных параллельных провода находятся в слабо
проводящей среде с удельным сопротивлением р. Расстояние
между осями проводов /, радиус сечения каждого провода а.
Найти для случая а«1:
а) плотность тока в точке, равноудаленной от осей проводов
на расстояние г, если разность потенциалов между проводами
равна U;
б) сопротивление среды на единицу длины проводов.
2.167. Зазор между обкладками плоского конденсатора
заполнен стеклом с удельным сопротивлением р = 100 ГОм м.
Емкость конденсатора С = 4,0нФ. Найти ток утечки через
конденсатор при подаче на него напряжения 1/ = 2,0кВ.
2.168. Два проводника произвольной формы находятся в
безграничной однородной слабо проводящей среде с удельным
сопротивлением р и диэлектрической проницаемостью е.
Найти значение произведения RC для данной системы, где
R — сопротивление среды между проводниками, С - взаимная
емкость проводников при наличии среды.
2.169. Проводник с удельным сопротивлением р граничит с
диэлектриком проницаемости е. В точке Л у поверхности
проводника электрическая индукция равна D, причем вектор D
направлен от проводника и составляет угол а с нормалью к
поверхности. Найти поверхностную плотность зарядов на проводнике вблизи точки А и плотность тока в проводнике вблизи этой точки.
2.170. Зазор между пластинами плоского конденсатора
заполнен неоднородной слабо проводящей средой, удельная
проводимость которой изменяется в направлении, перпендику
лярном пластинам, по линейному закону от а1 = 1,0 пСм/м до
а2 = 2,0пСм/м. Площадь каждой пластины 5 = 230 см2, ширина
зазора d = 2,0 мм. Найти ток через конденсатор при напряжении
на нем U = 300 В.
2.171. Показать, что закон преломления линий постоянного
тока на границе раздела двух проводящих сред имеет вид
*ва2/*ва1= °2/°i» где °i и °2 ~ проводимости сред, ctj и а2 -углы между линиями тока и нормалью к поверхности раздела данным сред.
2.172. Два цилиндрических проводника одинакового сече
ния, но с удельными сопротивлениями р1 = 84н0мм и р2 =
= 50нОм*м прижаты торцами друг к другу. Найти заряд на границе раздела данных проводников, если в направлении от
проводника 1 к проводнику 2 течет ток 7 = 50 А.
2.173. Удельная проводимость среды изменяется только
вдоль оси х по- закону о = ао/(1 + а*), где ао = 22 нСм/м, а = = 5,0 10"4 м"1. Найти плотность избыточного заряда среды при протекании тока плотностью j = 1,00 А/м2 в положительном направлении оси х.
2.174. Зазор между обкладками плоского конденсатора
заполнен последовательно двумя диэлектрическими слоями 1 и
2 толщиной di i\ d2 с проницаемостями С] и е2 и удельными
сопротивлениями рг и р2. Конденсатор находится под постоян
ным напряжением U, причем электрическое поле направлено
от слоя 1 к слою 2. Найти а - поверхностную плотность
сторонних зарядов на границе раздела диэлектрических слоев
и условие, при котором а = 0.
2.175. Между пластинами 7 и 2 плоского конденсатора
находится неоднородная слабо проводящая среда. Ее диэлектри
ческая проницаемость и удельное сопротивление изменяются от
значений Cj, pt у пластины 1 до значений е2, р2 у пластины
2. Конденсатор подключен к постоянному напряжению, и через
него течет установившийся ток / от пластины 1 к пластине 2.
Найти суммарный сторонний заряд в данной среде.
2.176. Длинный проводник круглого сечения радиуса а
сделан из материала, удельное сопротивление которого зависит
только от расстояния г до оси проводника по закону р = а/г2, где а — постоянная. Найти:
а) сопротивление единицы длины такого проводника;
б) напряженность электрического поля в проводнике, при
которой по нему будет протекать ток I.
2.177. Конденсатор емкости С = 400 пФ подключили через
сопротивление R = 650 Ом к источнику постоянного напряжения
Uo. Через сколько времени напряжение на конденсаторе станет
U = 0,90 Uo?
2.178. Конденсатор, заполненный диэлектриком с проницае
мостью е =2,1, теряет за время т = 3,0 мин половину сообщенно
го ему заряда. Считая, что утечка заряда происходит только
через диэлектрическую прокладку, найти ее удельное сопротив
ление.
2.179. Цепь состоит из источника постоянной ЭДС Ш и
последовательно подключенных к нему сопротивления R и
конденсатора емкости С. Внутреннее сопротивление источника
пренебрежимо мало. В момент t = 0 емкость конденсатора
быстро (скачком) уменьшили в г\ раз. Найти ток в цепи как
функцию времени t.
2.180. Амперметр и вольтметр подключили последовательно
к батарее с ЭДС ^=6,0 В. Если параллельно вольтметру
подключить некоторое сопротивление, то показание вольтметра
уменьшается в ц = 2,0 раза, а показание амперметра во столько
же раз увеличивается. Найти показание
|
вольтметра после подключения сопротивления.
| R |
| Рис. 2.38 |
|
2.181. 
Найти разность потенциалов
cpj - <p2 между точками 7 и 2 схемы
(рис. 2.38), если ^=10 Ом, 7^ = 20 Ом,
?j = 5 В и?2 = 2,0 В. Внутренние сопро
тивления источников тока пренебре
жимо малы.
2.182. Два последовательно соеди
ненных одинаковых источника ЭДС
имеют различные внутренние сопро
тивления flj и 7^, причем R2>R1.
Найти внешнее сопротивление 7?, при котором разность потенциалов на клеммах одного из источников (какого именно?) равна нулю.
2.183. В цепи (рис. 2.39) ЭДС источ
ников пропорциональны их внутрен- Рис 239
ним сопротивлениям: i?=aR, a — постоянная. Сопротивление проводов пренебрежимо мало. Найти:
а) ток в цепи;
б) разность потенциалов между точками А и В.
| и, в |
| \ | ||
| \ | ||
| . \ | ч | |
| t | 1----- ( |
| 80 |
| 70 |
| 60 |
| 50 |
| 5 W Рис. 2.40 |
| о |
|
| Рис. 2.41 |
2.184. Резистор с сопротивлением R
и нелинейное сопротивление, вольт-ам
перная характеристика которого U = a\[l,
где а — постоянная, соединены после
довательно и подключены к напряжению
Uo. Найти ток в цепи.
2.185. На рис. 2.40 показана вольт-
амперная характеристика разрядного
промежутка дугового разряда. Найти
максимальное сопротивление резистора,
соединенного последовательно с дугой,
при котором дуга еще будет гореть, если
эту систему подключить к напряжению
U0 = S5 В.
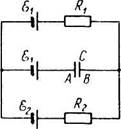
2.186. В схеме (рис. 2.41) ^ = 1,0 В,
^ = 2,5 В, /?j=10Om, R2 = 20Ou. Внут-
нренние сопротивления источников
пренебрежимо малы. Найти разность
потенциалов ipA - yB между обкладками
конденсатора С.
2.187. В схеме (рис. 2.42)? = 5,0В,
/?j = 4,0Om, &j = 6,0 Ом. Внутреннее со
противление источника Л = 0,10 Ом.
Найти токи, текущие через сопротивле
ния Rx и Rj.
U
q о-
Т* К
К
Рис. 2.42
Рис. 2.43
2.188. С помощью потенциометра (рис. 2.43) можно менять напряжение U, подаваемое на некоторый прибор с сопротивлением R. Потенциометр имеет длину I, сопротивление Rq и
находится под напряжением Uo, Найти зависимость U(x). Исследовать отдельно случай R»Rq.
2.189. Найти ЭДС и внутреннее сопротивление источника,
эквивалентного двум параллельно соединенным элементам с
ЭДС &х и %г и внутренними сопротивлениями Rx и R^.
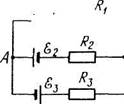
2.190. Найти значение и направление тока через резистор с
сопротивлением R в схеме (рис. 2.44), если Шх = \$ В, ^ = 3,7 В,
J?j=10Om, Л; = 20 Ом, Л = 5,0 Ом. Внутренние сопротивления
источников пренебрежимо малы.
|
6,
В
Рис. 2.44
Рис. 2.45
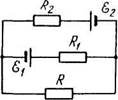
2.191. В схеме (рис. 2.45) ^ = 1,5 В, ^2 = 2,0В, ^3 = 2'5В>
^=10 Ом, Лг = 20Ом, /?j = 30Om. Внутренние сопротивления
источников пренебрежимо малы. Найти:
а) ток через резистор с сопротивлением Rx;
б) разность потенциалов ФЛ-фв между точками А и В.
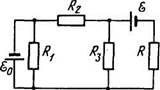
2.192. Найти ток через резистор с сопротивлением R в
схеме (рис. 2.46). Внутренние сопротивления источников пре
небрежимо малы.
А" 8
|
Рис. 2.46
Рис. 2.47
2.193. Найти разность потенциалов <рл - <рв между обкладками
конденсатора С схемы (рис. 2.47). Внутренние сопротивления источников пренебрежимо малы.
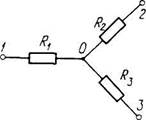
2.194. Найти ток через резистор Rt участка цепи (рис. 2.48), если #j=10Om, &j = 20 Ом, 7^ = 30 Ом и потенциалы точек 1, 2, 3 равны cpj=10B, cp2 = 6B, ф3 = 5 В.
|
Рис. 2.48
Рис_ 2.49
Р.
В
2.195. Между точками А и В цепи (рис. 2.49) поддерживают
напряжение (/ = 20 В. Найти ток и его направление в участке
1-2, если Лх = 5,0Ом и 7^ = 10 Ом.
2.196. В схеме (рис. 2.50) найти сопротивление между точ
ками А и В, если ^=100 Ом и 7^ = 50 Ом.
R-, R.
R,
В
R
Рис. 2.50
Рис. 2.51
2.197. Найти зависимость от времени напряжения на
конденсаторе С (рис. 2.51) после замыкания в момент t = 0
ключа К.
2.198. Сколько теплоты выделилось в спирали с сопротивле
нием R = 75 Ом при прохождении через нее количества
электричества q = 100 Кл, если ток в спирали:
а) линейно убывал до нуля в течение Дг = 50 с;
б) монотонно убывал до нуля так, что через каждые
Дг=2,0 с он уменьшался вдвое?
2.199. К источнику постоянного напряжения с внутренним
сопротивлением Д^, подключили три одинаковых резистора,
112
| R ■CZh |
| R -cz> |
| |--- 1 _ |
каждый сопротивлением R, соединенных между собой, как показано на рис. 2.52. При ка- с ком значении R тепловая мощность, выделяемая на этом участке, максимальна?
| Рис. 2.52 |
2200. Убедиться, что распре
деление тока в параллельно
соединенных резисторах с сопротивлениями #г и /fj соответствует минимуму выделяемой на этом участке тепловой мощности.
2201. Аккумулятор с ЭДС % = 2,6 В, замкнутый на внешнее
сопротивление, дает ток /= 1,0 А. При этом разность потенциа
лов между его полюсами U = 2,0 В. Найти тепловую мощность,
выделяемую в аккумуляторе, и мощность, которую развивают,
в нем электрические силы.
2202. Электромотор постоянного тока подключили к
напряжению U. Сопротивление обмотки якоря равно R. При
каком токе через обмотку полезная
мощность мотора будет максимальной? -?
Чему она равна? Каков при этом КПД
мотора? '
| 2 4 6 Рис. 2.53 |
| U. В |
2.203. Лампочку, параллельно соединенную с резистором, сопротивление i которого Л =2,0 Ом, подключили к источнику с ЭДС ^=15 В и внутренним сопротивлением R. = 3,0 Ом. Найти мощность, выделяемую на лампочке, „ если зависимость тока от напряжения на ней имеет вид, показанный на рис. 2.53.
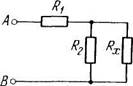2204. В схеме (рис. 2.54) R1 = 20 Ом
и #2 = 30 Ом. При каком сопротивлении
Rx выделяемая на нем тепловая мощность практически не будет зависеть от малых изменений этого сопротивления? Напряжение между точками А и В постоянное.
2205. В схеме (рис. 2.55) известны Рис 2.54
Rx, &;, Шу и %г. Внутренние сопро
тивления источников пренебрежимо малы. При каком сопротив
лении R выделяемая на нем тепловая мощность максимальна?
Чему она равна?
|
Рис. 2.55
Рис. 2.56
2206. Конденсатор емкости С = 5,00 мкФ подключили к
источнику постоянной ЭДС ^ = 200 В (рис. 2.56). Затем переклю
чатель К перевели с контакта 1 на контакт 2. Найти количес
тво теплоты, выделившееся на резисторе с сопротивлением
RX = 5QO Ом, если /tj = 330 Ом.
2207. Между обкладками плоского конденсатора помещена
параллельно им металлическая пластинка, толщина которой
составляет т| = 0,60 зазора между обкладками. Емкость конденса
тора в отсутствие пластинки С = 20нФ. Конденсатор подключи
ли к источнику постоянного напряжения U = 100 В и пластинку
извлекли из конденсатора. Найти:
а) приращение энергии конденсатора;
б) механическую работу, совершенную против электрических
сил при извлечении пластинки.
2208. Стеклянная пластинка целиком заполняет зазор между
обкладками плоского конденсатора, емкость которого в отсут
ствие пластинки С-20 нФ. Конденсатор подключили к источни
ку постоянного напряжения U = 100 В и пластинку извлекли из
зазора. Найти приращение энергии конденсатора и механичес-
кескую работу, совершенную против электрических сил при извлечении пластинки.
2209. Цилиндрический конденсатор,
подключенный к источнику постоянного
напряжения U, касается своим торцом
поверхности воды (рис. 2.57). Расстояние
d между обкладками конденсатора значи
тельно меньше их среднего радиуса.
Найти высоту h, на которой установится
; уровень воды между обкладками конден-
■ сатора. Капиллярными явлениями прене-
Рис. 2.57 бречь.
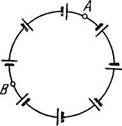
2210. Радиусы обкладок сферического конденсатора равны
а и Ь, причем а<Ъ. Пространство между обкладками заполне
но однородным веществом диэлектрической проницаемости е
и удельным сопротивлением р. Первоначально конденсатор не
заряжен. В момент г = 0 внутренней обкладке сообщили заряд
q0. Найти:
а) закон изменения во времени заряда на внутренней
обкладке;
б) количество теплоты, выделившейся при растекании
заряда.
2211. Обкладкам конденсатора емкости С = 2,00 мкФ сообщи
ли разноименные заряды д0 = 1,ООмКл. Затем обкладки
замкнули через сопротивление Л = 5,0МОм. Найти:
|
а') заряд, прошедший через это сопротивление за г = 2,00 с; б) количество теплоты, выделившейся в сопротивлении за то же время.
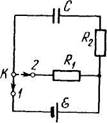
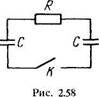
2212. В схеме, показанной на рис. 2.58,
один конденсатор зарядили до напряжения
Uo и в момент t = 0 замкнули ключ К.
Найти:
а) ток в цепи как функцию времени I (t);
б) количество выделившейся теплоты,
зная / (f).
2213. Катушка радиуса г = 25 см, содержащая I = 500 м
тонкого медного провода, вращается с угловой скоростью ы =
= 300 рад/с вокруг своей оси. Через скользящие контакты
катушка подключена к баллистическому гальванометру. Общее
сопротивление всей цепи Л = 21 Ом. Найти удельный заряд
носителей тока в меди, если при резком затормаживании
катушки через гальванометр проходил заряд q = 10 нКл.
2214. Найти суммарный импульс электронов в прямом
проводе длины 1 = 1000 м с током / = 70 А,
2.215. По прямому медному проводу длины / = 1000 м и
сечения 5 = 1,0 мм2 течет постоянный ток / = 4,5 А. Считая, что на каждый атом меди приходится один свободный электрон, найти:
а) время, за которое электрон переместился от одного конца
провода до другого;
б) сумму электрических сил, действующих на все свободные
электроны в данном проводе.
2216. Однородный пучок протонов, ускоренный разностью потенциалов 1/ = 600кВ, имеет круглое сечение радиуса
г = 5,0 мм. Найти напряженность электрического поля на поверхности пучка и разность потенциалов между поверхностью и осью пучка при токе / = 50 мА.
2217. Две большие параллельные пластины находятся в вакууме. Одна из пластин служит катодом — источником электронов, начальная скорость которых пренебрежимо мала. Электронный поток, направленный к противоположной пластине, создает в пространстве объемный заряд, вследствие чего потенциал в зазоре между пластинами меняется по закону
Ф = ах413, где а - положительная постоянная, х — расстояние от катода. Найти:
а) плотность пространственного заряда р (х);
б) плотность тока.
2.218. Воздух между двумя параллельными пластинами, отстоящими друг от друга на расстояние d = 20 мм, ионизируют рентгеновским излучением. Площадь каждой пластины
S = 500 см2. Найти концентрацию положительных ионов, если при напряжении U = 100 В между пластинами идет ток / = = 3,0 мкА, значительно меньший тока насыщения. Подвижность
ионов воздуха ио+ = 1,37 см2/(Вс) и и„" = 1,91 см2/(Вс).
|
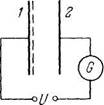
2219. Газ ионизируют непосредственно у
поверхности плоского электрода 1 (рис. 2.59),
отстоящего от электрода 2 на расстояние I.
Между электродами приложили переменное
напряжение, изменяющееся со временем t
по закону U= Uo sin со г. Уменьшая частоту
w, обнаружили, что гальванометр G показы
вает ток только при о < о0, где «0 - неко-
Р 259 торая граничная частота. Найти подвиж-
ность ионов, достигающих при этих условиях 2.
2220. Воздух между двумя близко расположенными пласти
нами равномерно ионизируют ультрафиолетовым излучением.
Объем воздуха между пластинами V = 500 см3, наблюдаемый ток насыщения ^нас = 0,48 мкА. Найти:
а) число пар ионов, создаваемых ионизатором за единицу времени в единице объема;
_ б) равновесную концентрацию пар ионов, если коэффициент
рекомбинации ионов воздуха г = 1,67-10~6 см3/с.
2221. Длительно действовавший ионизатор, создававший за
единицу времени в единице объема воздуха число пар ионов
п(=3,5 1(Р см"3 с"1, был выключен. Считая, что единственным 116
процессом потери ионов в воздухе является рекомбинация с
коэффициентом г = 1,67 • 10"6 см3/с, найти, через какое время после выключения ионизатора концентрация ионов уменьшится
в г\ = 2,0 раза.
2222. Плоский воздушный конденсатор, расстояние между
пластинами которого d = 5,0 мм, зарядили до 17 = 90 В и
отключили от источника напряжения. Найти время, за которое
напряжение на конденсаторе уменьшится на ti = 1,0%, имея в
виду, что в воздухе при обычных условиях в среднем образует
ся за единицу времени в единице объема число пар ионов
л; = 5,0 см"3-с"1 и что данное напряжение соответствует току насыщения.
2223. Между двумя плоскими пластинами конденсатора,
отстоящими друг от друга на расстояние d, находится газ.
Одна из пластин эмигрирует ежесекундно v0 электронов,
которые, двигаясь в электрическом поле, ионизируют молекулы
газа так, что каждый электрон создает на единице длины пути
а новых электронов (и ионов). Найти электронный ток у
противоположной пластины, пренебрегая ионизацией молекул
газа ионами.
2224. Газ между пластинами конденсатора, отстоящими друг
от друга на расстояние d, равномерно ионизируют ультрафииле-
товым излучением так, что ежесекундно в единице объема
создается п. электронов. Последние, двигаясь в электрическом
поле конденсатора, ионизируют молекулы газа, причем каждый
электрон создает на единице длины своего пути а новых
электронов (и ионов). Пренебрегая ионизацией ионами,
найти плотность электронного тока у пластины с большим
потенциалом.
Дата добавления: 2015-08-02; просмотров: 635 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проводники и диэлектрики в электрическом поле | | | Постоянное магнитное поле. Магнетики |