
Читайте также:
|
Вычислим результирующие силы, действующие со стороны среды на единицу длины поверхности цилиндра при обтекании его потоком идеальной среды с циркуляцией. Для этого найдём распределение давления по поверхности цилиндра в соответствии с первым уравнением (7.6.12), имея ввиду, что при r = r 0 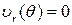 и
и 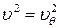 :
:
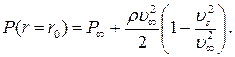 (7.7.5)
(7.7.5)
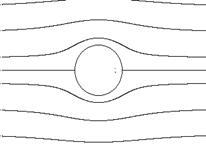 а). Г = 0
а). Г = 0
| 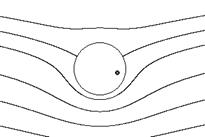 б).
б). 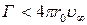
|
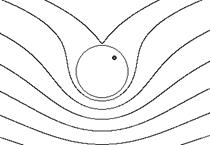 в).
в). 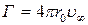
| 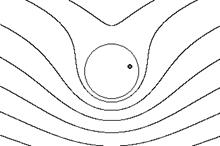 г).
г). 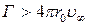
|
Рис. 7.20
Подставляя в (7.6.19) скорость 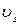 на поверхности цилиндра (7.6.17), получим:
на поверхности цилиндра (7.6.17), получим:
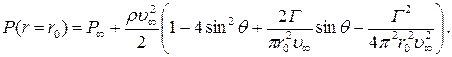 (7.7.6)
(7.7.6)
Силу сопротивления 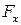 и подъёмную силу
и подъёмную силу 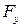 возможно вычислить согласно (7.6.13) и (7.6.14):
возможно вычислить согласно (7.6.13) и (7.6.14):
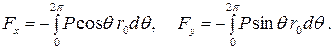 (7.7.7)
(7.7.7)
После подстановки (7.7.6) в (7.7.7) и интегрировании по углу 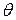 в пределах от
в пределах от 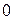 до
до 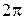 следует:
следует:
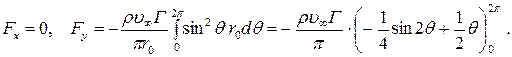 (7.7.8)
(7.7.8)
Как и прежде, для силы лобового сопротивления имеет место парадокс Даламбера, т.е. 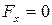 . Однако циркуляция стимулирует возникновение подъёмной силы, которая направлена в сторону, противоположную направлению оси y (рис. 7.20), и равна
. Однако циркуляция стимулирует возникновение подъёмной силы, которая направлена в сторону, противоположную направлению оси y (рис. 7.20), и равна
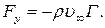 (7.7.9)
(7.7.9)
Дата добавления: 2015-08-03; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обтекание бесконечного цилиндра с циркуляцией | | | Эффект Магнуса |