Постановка задачи и сущность метода

Суперпозицию плоских потенциальных потоков можно осуществлять и графически. Представим себе, что на плоскости нанесены линии тока каких-либо двух плоских потоков (рис. 7.22). Можно в точках пересечения линий тока построить в одинаковом масштабе вектора скоростей движений среды в обоих потоках. Очевидно, скорость результирующего движения в этих точках изобразится диагональю параллелограмма, построенного на векторах, изображающих скорости отдельных движений. Причем такое построение будет тем точнее, чем чаще нанесены линии тока рассматриваемых потоков.

Рассмотрим вопрос о масштабах изображения слагаемых потоков. Для этого обратимся к рис. 7.23. В пределах малых участков линий тока их можно считать прямыми. Для того чтобы отрезки и 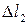изображали модули скоростей и в одинаковых масштабах, необходимо, чтобы выполнялись следующие условия:

Из подобия прямоугольных треугольников получаем:

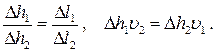(7.8.1.22)

Рис. 7.22

Рис. 7.23

Но произведение определяет расход среды между двумя соседними линиями тока ψ ₁ первого потока, а произведение расход среды между двумя соседними линиями тока ψ ₂ второго потока. Поэтому, для того чтобы масштабы изображений складываемых потоков были одинаковыми, необходимо, чтобы расходы среды между двумя соседними линиями тока в обоих движениях были равны, т.е.

(7.8.2.23)

Рис. 7.24

Рассмотрим в качестве примера суперпозицию двух потоков - прямолинейного поступательного потока и плоского источника. Очевидно, что в плоском источнике линии тока представлены радиусами, проведёнными из точки, в которой расположен источник (рис. 7.24). Эквипотенциальные линии () представляют собой окружности с центром в источнике. Если мощность источника равна , то,

принимая во внимание, что в таком движении скорость среды в любой точке направлена вдоль радиусов, проведённых из центра источника, скорость потока на расстоянии r от источника равна:

(7.8.3.24)

Будем предполагать, что оба потока изображены в одном масштабе, т.е. расход жидкости между двумя соседними линиями тока прямолинейного поступательного потока равен расходу жидкости между соседними линиями тока плоского источника (рис. 7.25).

Рассмотрим линию тока ОО₁ прямолинейного поступательного потока, проходящую через центр плоского источника О. Так как скорость этого потока

Рис. 7.25

постоянна и равна , а скорость вдоль линии тока плоского источника возрастает неограниченно с приближением к его центру согласно (7.6.24), то на линии ОО₁ всегда найдется точка А, в которой результирующая скорость равна нулю. Откладывая затем в точках пересечения линий тока двух потоков значения скоростей и , модуль которой вычислен согласно (7.6.24); для заданного угла 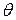по найденному графически или расчётному значению r можно по правилу параллелограмма вычислить скорость суммарного движения. Причем эти суммарные вектора скоростей являются касательными к линии тока ВА.

Линия АВ разграничивает среду, вытекающую из источника О, от набегающего потока. Так как при обтекании идеальной средой поверхность тела также является граничной линией тока, через которую среда не протекает, то можно линию АB отождествить с линией, которая описывает контур некоторой твердой поверхности, обтекаемой прямолинейным поступательным потоком. Вычисляя скорости отдельных движений в каждой точке пересечения линий тока двух потоков, можно найти в этих точках скорость результирующего движения. Воспользовавшись формулой Бернулли, можно вычислить давление в каждой точке потока, в том числе и на поверхности обтекаемого тела, изображаемой на плоскости линией АB. Суммируя силы давления, действующие на элементы поверхности тела, можно найти результирующую силу, действующую на обтекаемое тело.

Таким образом, комбинация плоскопараллельного поступательного потока с источниками и стоками позволяет получить картину обтекания некоторого замкнутого контура, форма которого может быть довольно сложной в зависимости от интенсивности отдельных слагаемых движений. Добавление еще нескольких источников и стоков различной мощности позволит представить картину обтекания тела практически любой формы. Конечно, все операции сложения потенциальных потоков можно провести и аналитически. Однако во многих случаях графический метод может дать достаточно точный, а главное наглядный результат, необходимый для решения некоторой конкретной практической задачи.

Дата добавления: 2015-08-03