Распределение давления около движущегося цилиндра

Найдем распределение давления на поверхности цилиндра. Для этого воспользуемся уравнением Бернулли в форме (7.5.3), в котором для рассматриваемого нестационарного потенциального движения идеальной среды в отсутствии массовых сил баротропный потенциал равен Ф(P)=P/ρ:

(7.9.9)

Так как на бесконечности жидкость покоится, т.е. и , то давление P (r) в любой точке среды равно

(7.9.10)

Из (7.9.6) следует, что потенциал скорости 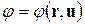в нестационарной постановке может явно или неявно зависеть от времени t, т.-е., если потенциал j и зависит от времени, то неявно через зависимость от времени скорости движения индивидуальной частицы, т.е. u = (r, t). Формула (7.9.8) описывает зависимость потенциала j и от координаты точки 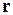около цилиндра в тот же момент времени. Зависимость 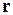от времени очевидная, если характеризует точку в неподвижной системе координат. Но в такой нестационарной постановке задачи вся стационарная картина обтекания движется в неподвижной системе координат со скоростью , поэтому . Дифференцируя потенциал j по времени t как сложную функцию, получаем

(7.9.11)

Используя (7.9.6), можно получить слагаемые в правой части (7.9.11) в виде:

Таким образом, производная равна

(7.9.12)

На поверхности цилиндра () производная равна

(7.9.13)

Квадрат модуля скорости с использованием (7.9.8) равен

(7.9.14)

Подставляя полученные выражения (7.9.13, 14) в (7.9.10), получим следующую формулу для распределения давления по поверхности цилиндра:

(7.9.15)

Если движение цилиндра стационарное, т.е. 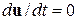, то из (7.9.15) следует:

(7.9.15а)

При давление на поверхности цилиндра в точках С и D равно давлению в набегающем потоке (сравни с рис.7.18). При давление является наибольшим и наименьшим соответственно:

. (7.9.15б)

Таким образом, в отличие от обтекания неподвижного цилиндра при движении цилиндра с постоянной скоростью u силы давления со стороны идеальной среды стремятся «сжать» его в направлении, перпендикулярном движению, и растянуть в направлении движения, т.е. среда как бы препятствует.

движению цилиндра.

Дата добавления: 2015-08-03