Многочлен значений ошибок

Он определяется через S(x) и Λ(х) в соответствии с видом введенного выше многочлена ошибок Ω(x)=S(x)* Λ (x) (mod x^2t)=

=[(S₁x⁰+ S₂x¹+…+ S_2t x^2t-1) ] (mod x^2t)=

=[(Y₁X₁+ Y₂X₂+…+ Y_vX_v,)x⁰ +(Y₁X₁²+ Y₂X₂²+…+ Y_vX_v²)x¹ +…

+(Y₁X₁^2t+ Y₂X₂^2t+…+ Y_vX_v^2t)x^2t-1 ](mod x^2t)=

=[ Y₁X₁(1+ X₁x +X x²+…+X x^2t-1) +

+ Y₂X₂(1+ X₂x +X x²+…+X 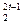x^2t-1) +...

.+ Y_vX_v (1+ X_v x +X x²+…+X x^2t-1) ](mod x^2t)=

=[ Y₁X₁(1+ X₁x +X x²+…+X x^2t-1)(1+X₁x) +…

+ Y_vX_v (1+ X_v x +X x²+…+X x^2t-1)(1+ X_v x) ](mod x^2t)=

=[ Y₁X₁ (1+X₁x)^2t +…+ Y_vX_v(1+ X_v x)^2t ](mod x^2t)=

=[ Y₁X₁ +…+ Y_vX_v ] = .

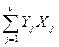
=[ Y₁X₁ (1+(X₁x)^2t) +…+ Y_vX_v(1+(X_v x))^2t ](mod x^2t)=

Итак, многочлен значений ошибок выражается через значения ошибок и локаторы ошибок следующим образом:

Ω(х) = .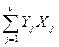

Выражение для Ω(х) определяет множества из 2t-v уравнений и называется ключевым уравнением, так как оно является ключом решения задачи декодирования.

Ключевое уравнение позволяет получить v уравнений для v неизвестных коэффициентов Λ(x). Эти уравнения являются линейными. Они могут быть решены обычными методами, либо с помощью итерационных процедур. После нахождения Λ(х) ключевое уравнение позволяет найти неизвестные компоненты многочлена е (х ) и по ним переданную кодовую комбинацию f(x)=C(x)+e(x).

Из изложенного можно сделать вывод, что декодирование кодов БЧХ на основе решения ключевого уравнения распадается на два этапа.

I этап — вычисление многочлена локатора ошибок Λ(х).Для двоичных кодов БЧХ этим этапом декодирование завершается.

II этап - для недвоичных кодов, какими являются РС-коды, вычисление многочлена значений ошибок Ω(х), позволяющего вычислять значение каждой из υ ошибок в принятой комбинации.

Для нахождения многочлена локаторов ошибок из литературы известны три алгоритма:

1. Алгоритм Питерсона.

2. Алгоритм Берлекемпа-Месси.

3- Алгоритм Евклида - алгоритм СКХН.

Авторы первого и второго алгоритмов указаны в их названии. Алгоритм Евклида для целей решения ключевого уравнения был впервые предложен четырьмя авторами: Сугияма, Касахара, Хирасава и Намекава. В дальнейшем для краткости будем называть алгоритмом Евклида.

Алгоритм Питерсона может быть использован как самостоятельная процедура декодирования недвоичных циклических кодов и на II этапе.

Алгоритм Берлекемпа-Месси и алгоритм Евклида на II этапе декодирования для недвоичных циклических кодов дополняют алгоритмом Форни, позволяющим по корням Λ (х ) и многочлену Ω(x) найти значения ошибок. Сочетание алгоритма Берлекемпа-Месси и алгоритма Форни получило название быстрого декодирования кодов БЧХ.

Рассмотрим сущность изложенных алгоритмов декодирования

Дата добавления: 2015-08-02