Схемы кодирующих устройств циклических кодов

а) Кодирование по g(x)

В основе кодирующего устройства лежит схема деления на порождающий многочлен g(x) степени n-k с предварительным умножением на . Данная схема строится на основе схемы, представленной на рис. 6.6 и в общем случае имеет вид, изображенный на рис. 6.10. Число ячеек памяти в регистре равно n-k, т.е. числу избыточных элементов в кодовой комбинации. Обратные связи подключены в соответствии с ненулевыми коэффициентами g(x), следовательно, общее число обратных связей равно числу компонентов g(x) (или весу в двоичном представлении). Число сумматоров по модулю 2 равно числу знаков “+” в записи g(x) в виде многочлена.

Вход схемы подключен после ячейки для осуществления предварительного умножения кодируемого сообщения на . Схема работает следующим образом. Информационные символы поступают на вход кодирующего устройства, начиная со старшей степени, и одновременно на выход схемы – в канал связи. В это время на схему И₁ в цепи обратной связи поступают k тактовых импульсов и со входа информационные импульсы поступают через цепь обратной связи в разряды регистра . Как только все k информационных символов поступят в устройство, совокупность n-k - символов в разрядах регистра совпадет с остатком от деления на g(x), т.е. разряды регистра содержат проверочные символы r(x) кодовой комбинации.

По прошествии k тактов подача тактовых импульсов в схему И₁ прекращается, т.е. линия обратной связи разрывается и n-k проверочных символов, сформированных в регистре, через схему И₂, на которую начинают поступать тактовые импульсы от (k +1)-го до n- го такта, выводятся в канал связи сразу же за информационными элементами.

Таким образом, за n тактов с выхода схемы в канал поступает вся кодовая комбинация циклического (n,k) – кода.

Пример 6.16. Построить кодирующее устройство для циклического кода (7,4) с порождающим многочленом и проследить по тактам процесс формирования кодовой комбинации.

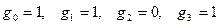В соответствии с рис 6.10 и видом g(x) составляем схему кодирующего устройства, которая содержит разряды и обратные связи , (рис 6.11).

Рассмотрим по тактам процесс кодирования некоторой произвольной комбинации простого кода, например, 0101. Результат представлен в таблице 6.4.

Таблица 6.4

№ такта	Вход	Содержимое r0	Содержимое r1	Содержимое r2	Выход И1	Выход	Примечание
4	-					-	Тактовые импульсы поступают на И1 Тактовые импульсы поступают на И2

Для оценки правильности процесса кодирования определим алгебраически комбинацию циклического (7,4) – кода, соответствующую рассмотренной комбинации простого кода

.

Находим

Разделив на g(x), получим проверочные элементы кодовой комбинации:

+

+

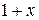
В результате решения получим и .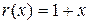

Следовательно, соответствующая кодовая комбинация есть

б) Кодирование по h(x)

Кодирующее устройство для циклического (n,k) – кода может быть построено на основе схемы для решения рекуррентных соотношений (рис. 6.7). Структурная схема кодирующего устройства для этого случая представлена на рис. 6.12. В основе схемы лежит регистр сдвига из k ячеек, обратные связи построены в соответствии с видом h(x) и их число определяется числом ненулевых компонент в h(x) (или весом h(x) в двоичном представлении), число сумматоров по модулю 2 на 1 меньше число знаков “+” в записи h(x) в виде многочлена.

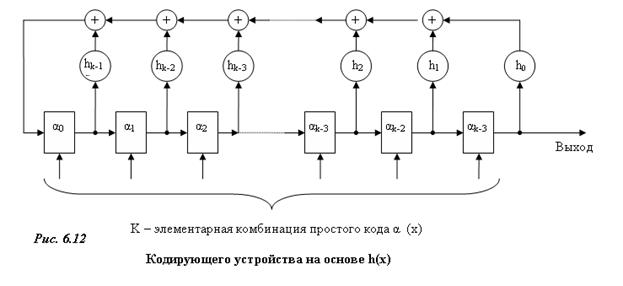
Информационные элементы (элементы комбинации простого кода) а(х) помещаются в k разрядах регистра в соответствии с нумерацией ячеек регистра. Затем производится n сдвигов. Первые k элементов, появившиеся на выходе, есть информационные элементы комбинации циклического кода, а последние n-k элементов – проверочные.

В совокупности за n тактов с выхода схемы в канал связи поступает кодовая комбинация длины n.

Пример 6.17. Для циклического (7,4) – кода предыдущего примера построить кодирующее устройство по h(x) и проследить по тактам процесс формирования кодовой комбинации.

Находим .

Регистр содержит разряды и имеет связи

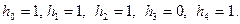
Вид кодирующего устройства, построенного по данному способу для кода (7,4) с представлен на рис. 6.13.

Рассмотрим процесс формирования кодовой комбинации, соответствующей комбинации простого кода 0101. Этапы формирования кодовой комбинации сведем в таблицу 6.5.

Таблица 6.5

№ такта	Содержимое разрядов регистра	Выход 1	Выход 2	Выход
							-

Таким образом, на выходе кодирующего устройства получена та же самая комбинация, что и в предыдущем примере.

Указанные способы построения кодирующих устройств позволяют производить их реализацию при использовании минимального числа переключательных элементов для любого соотношения n и k.

При удобно строить кодирующее устройство по g(x). Если же , то способ по h(x) - предпочтительнее.

Дата добавления: 2015-08-02