Определение циклического кода

Среди многообразия групповых кодов особое место занимают циклические (n,k) - коды. Циклические коды отличаются простотой реализации, возможностью построения кода любой длины с известными корректирующими свойствами, рациональным соотношением между избыточностью и корректирующей способностью (в этом отношении они близки к границе Хэмминга).

Определение 1. Циклическим кодом называют, групповой (n, k) – код, обладающий следующим свойством: для любой кодовой комбинации этого кода комбинация , полученная циклическим сдвигом элементов на единицу вправо, также принадлежит этому коду.

Описание циклических кодов основывается на представлении кодовых комбинаций в виде многочленов от одной неизвестной с коэффициентами в виде двоичных элементов 0 и 1, т.е. элементов поля GF(2). Используя такое представление, можно дать следующее, эквивалентное приведенному выше, определение циклического кода.

Определение 2. Циклическим (n, k) – кодом называется код, множество кодовых комбинаций которого представляется совокупностью многочленов степени n-1 и менее, делящихся на некоторый многочлен g(x) степени (n-k), являющийся сомножителем двучлена .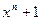

Доказательство эквивалентности этих двух определений основывающееся на представлении циклического кода как идеала кольца классов вычетов многочленов по модулю двучлена 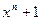.(см. свойства 3 и 4 кольца). Групповая структура циклических кодов определяется тем, что, во-первых, операция сложения многочленов совпадает с операцией сложения векторов, во-вторых, совокупность многочленов, делящихся на некоторый многочлен g(x), должна быть замкнута в отношении операции сложения, т.к., если каждое из слагаемых делится на g(x), то их сумма делится на g(x) и степень суммы не старше степеней слагаемых, в-третьих, нулевая комбинация принадлежит циклическому коду, т.к. 0 делится без остатка на g(x).

Структура циклического кода не будет раскрыта полностью, если не учитывать, что свойство цикличности эквивалентно заданию действия умножения над кодовыми комбинациями как над многочленами и замкнутости кодовых комбинаций по этому действию. Для обеспечения замкнутости кодовых комбинаций в пределах множества многочленов степени n -1 и менее умножение кодовых комбинаций необходимо производить по модулю двучлена 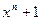. Из определения 2 следует, что к циклическому коду относятся лишь многочлены степени n -1 и менее, кратные многочлену g(x). Структура циклического кода формируется в результате следующих построений. Бесконечное множество многочленов произвольных степеней путем вычисления остатков от деления на 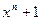(приведения по модулю 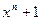) раскладывается на конечное число множеств, обладающих одинаковым остатком, называемых классами вычетов.

При этом каждый многочлен степени от нулевой до (n -1)-ой включительно принадлежит своему определенному классу вычетов и полностью его представляет. Классы вычетов при таком разложении играют ту же роль, что и смежные классы в разложении группы по подгруппе. В данном случае роль подгруппы играет класс вычетов, содержащий все многочлены, кратные 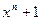, т.е. и т.д. Общее число классов вычетов равно числу всевозможных многочленов степени n -1 и менее, т.е. 2 ⁿ.

Разложение бесконечного множества многочленов на классы вычетов по модулю 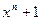единственно и каждый класс вычетов однозначно определяется любым многочленом, принадлежащим данному классу. Это относится и к первому классу вычетов, содержащему 0 и 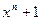, который по отношению к остальным классам вычетов рассматривается как единичный элемент, т.е. . (Аналогично тому, как при сложении по модулю 2 принимается 2=0). Полное множество классов вычетов рассматривается как множество всех комбинаций длины n их представляющих. В качестве кодовых комбинаций рассматриваются те классы вычетов, которые содержат многочлены, кратные g(x), и совокупность всех многочленов, кратных g(x), как было показано выше, в свою очередь образует подгруппу (идеал) множества всех классов вычетов многочленов по модулю 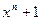. Следовательно, классы вычетов многочленов в свою очередь могут быть разложены на смежные классы по подгруппе, образующей циклический код. Так как 0 принадлежит к этой подгруппе, то по отношению ко всем смежным классам разложения классов вычетов по подгруппе, образующей код, справедливо , где произвольный многочлен кольца классов вычетов многочленов по модулю 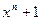. Нетрудно показать, что g(x) должен быть делителем .

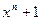Действительно, поскольку по определению g(x) имеет степень, меньшую, чем n, то можно записать результат деления 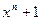на g(x) в виде следующего равенства

, где

- остаток от деления, степень которого меньше степени g(x), а q(x) - частное от деления. Учитывая, что , получаем , а так как мы установили выше, что 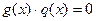, то и 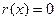, т.е. g(x) делит 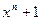без остатка. Значит, g(x) – сомножитель двучлена .

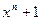Многочлен g(x) принято называть порождающим или образующим многочленом циклического кода. С другой стороны циклический (n, k) – код может быть задан через двойственный (n, n-k) – код, порожденный многочленом Так как , то о ртогонален g(x) и называется проверочным многочленом.

Пример 6.3. Дано .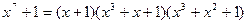

Найти все циклические (n, k) – коды с n = 7, которые могут быть построены на основе данного разложения. Определим все сомножители , которые и будут являться порождающими многочленами искомых кодов. Возможные сомножители и соответствующие им коды перечислены в следующей таблице.

Сомножитель	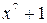Код
	(7,6)
	(7,4)
	(7,4)
	(7,3)
	(7,3)
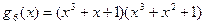
	(7,1)

Каждый сомножитель двучлена 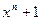может быть выбран в качестве порождающего многочлена циклического кода длины n.

Однако не любой сомножитель порождает циклический (n, k) – код с требуемыми корректирующими свойствами. Методика выбора порождающего многочлена для построения циклического кода с заданными корректирующими свойствами будет рассмотрена ниже.

Дата добавления: 2015-08-02