Коды Хэмминга

Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H_(n,k), имеющей строк и 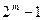столбцов, причем столбцами H_(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до ).

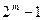Длина кодовой комбинации кода Хэмминга равна .

Число информационных элементов определяется как .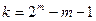

Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.

Зная вид матрицы H_(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбца H_(n,k) не являются линейно зависимыми. Наряду с этим, для любого числа m всегда можно указать три столбца матрицы H_(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэмминга d_min =3.

Код Хэмминга является одним из немногочисленных примеров совершенного кода.

Действительно, поскольку (n, k) – код Хэмминга исправляет все одиночные ошибки, то все образцы одиночных ошибок (а их всего насчитывается вариантов) должны разместиться в различных смежных классах, число которых также равно 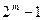. Следовательно, помимо смежных классов, содержащих образцы одиночных ошибок, никаких других в таблице декодирования не имеется, что и подтверждает совершенность кода Хэмминга.

При фиксированном числе можно построить код Хэмминга любой длины () путем укорочения (n, k) – кода. Укорочение не уменьшает минимальное кодовое расстояние. В силу того, что для любого числа n существует код Хэмминга, любой групповой код с исправлением одиночных ошибок принято называть кодом Хэмминга.

Пример 5.13. Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.

m		k
			0,33
			0,57
			0,74
			0,84
			0,91
			0,95

и т.д.

Очевидно, что минимальная длина кода Хэмминга, имеющего практическое значение, есть 3. При увеличении n отношение возрастает и стремится к 1.

Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:

.

Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3(к примеру 1, 2 и 3), следовательно, d_min =3.

В том случае, когда столбцы матрицы H_(n,k) – кода Хэмминга есть упорядоченная запись m – разрядных двоичных чисел, декодирование осуществляется оригинальным образом. В результате вычисления проверочного соотношения для кодовой комбинации , имеющей одиночную ошибку, получается синдром в точности равный номеру элемента, в котором произошла ошибка.

Действительно, если e_i содержит одну единицу в разряде, соответствующем ошибочному элементу, то при умножении на матрицу Н^Т все строки матрицы Н^Т, соответствующие нулям в e_i, обращаются в нули, и лишь строка, соответствующая “1” в e_i сохраняет свой вид (т.е. порядковый номер элемента в двоичной записи) в ответе.

Пример 5.15. Пусть приемник УЗО системы передачи данных зарегистрировал комбинацию . Вычисление синдрома дает

,

т.е. ошибка в четвертом элементе и кодовая комбинация кода (7,4), которая была передана, имеет вид:

Путем несложных преобразований из (n, k) – кода Хэмминга с d_min =3 можно получить (n +1, k) – код Хэмминга с d_min =4.

Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.

Матрица проверок для (n +1, k) – кода Хэмминга с d_min =4 получается из матрицы проверок (n, k) – кода с d_min =3 путем введения дополнительной строки из (n +1)-ой единицы.

Так как размерность матрицы проверок кода с d_min =4 должна быть равна , то к каждой строке матрицы проверок кода с d_min =3, необходимо добавить один нулевой элемент для того, чтобы не нарушить введенные ранее проверки. Матрица проверок для (n +1, k) – кода d_min =4 имеет вид:

,

где H_(n,k) = матрица проверок исходного кода с d_min =3.

Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.

Пример 5.16. Построить код Хэмминга (8,4) с d_min =4 на основе матрицы проверок кода (7,4).

Известно:

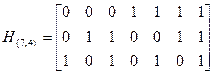
По виду матрицы 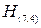можно сделать вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на четность.

Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.

Таким образом, матрице 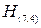соответствует следующая система проверочных соотношений:

Для того, чтобы получить код (8,4) с d_min =4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:

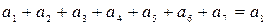
или

.

Этой проверке соответствует дополнительная (четвертая) строка в матрице Н _(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н _(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:

.

Определим известным способом d_min (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) d_min =4.

До сих пор мы еще не разделили элементы кодовой комбинации на информационные и проверочные. Наиболее рационально, по-видимому, это можно сделать следующим образом. Желательно, чтобы каждое проверочное соотношение однозначно определяло проверочный элемент как результат проверки на четность некоторой совокупности информационных элементов. В таком случае мы получили бы возможность определять значение проверочного элемента наиболее простым образом – решением одного линейного уравнения с одним неизвестным. Для этого при упорядоченной записи столбцов матрицы H_(n,k) в качестве проверочных элементов необходимо брать элементы с номерами 2 ⁱ, где i изменяется от 0 до m -1, так как именно эти столбцы содержат только по одной единице. Последнее свидетельствует о том, что элементы с номерами 2 ⁱ входят только в одну проверку и, следовательно, они могут быть взяты в качестве проверочных.

Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).

По виду матрицы 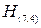, приведенной в предыдущем примере, в качестве проверочных элементов выбираем элементы, которым соответствуют столбцы, содержащие только по одной единице, т.е. первый, второй и четвертый. Следовательно, 4 информационных элемента кода (7,4) должны занимать места 3, 5, 6 и 7-го разрядов. Приведенная в предыдущем примере система проверочных соотношений позволяет определить значение каждого из проверочных элементов по значениям информационных элементов, т.е. по значению элементов простого кода, который необходимо закодировать кодом Хэмминга

Зная места проверочных элементов, легко привести матрицу H_(n,k) кода Хэмминга к канонической форме.

Для этого необходимо столбцы с номерами 2 ⁱ, где при упорядоченной записи столбцов переместить на места m первых столбцов в порядке убывания номеров. В общем виде такая перестановка столбцов в матрице H_(n,k) приводит к эквивалентному (n, k) – коду. В случае же кодов Хэмминга естественной длины код получается даже не эквивалентный, а в точности совпадающий с исходным кодом.

Пример 5.18. Преобразовать матрицу 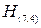к канонической форме.

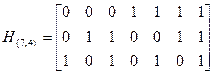
Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:

.

Это и есть каноническая форма матрицы 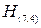. Сравнение ее с исходной матрицей 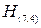показывает, что местам информационных элементов в канонической форме соответствуют столбцы с номерами 3, 5, 6, 7, а местам проверочных элементов - столбцы 4, 2, 1.

При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:

Порождающую матрицу G_{(n, k)} для кода Хэмминга можно получить из матрицы H_(n,k), используя теорему 5.3:

Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.

Оценим эффективность кодов Хэмминга.

а) Коды Хэмминга с dmin=3

Такие коды используются либо для исправления ошибки кратности t =1, либо для гарантийного обнаружения ошибок кратности S =2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:

.

Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:

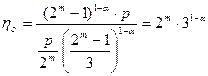
б) Коды Хэмминга с d_min=4.

Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:

Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:

.

Дата добавления: 2015-08-02