Выше мы рассматривали групповые коды, в которых задана операция поразрядного сложения по модулю 2. В ряде случаев для придания кодовым комбинациям дополнительных признаков используют поразрядное сложение по модулю 2 с инвертированием некоторых элементов. По отношению к групповому коду полученный код может быть отождествлен со смежным классом разложения группы по подгруппе, являющейся кодом, с образующим в виде комбинации с единицами на местах инвертируемых элементов и нулями во всех остальных разрядах.
В силу этого рассматриваемые коды получили название смежно-групповых.
Следует иметь в виду, что смежно-групповой код существует только в дискретном канале. Процедуры кодирования и декодирования при использовании смежно-групповых кодов осуществляются как аналогичные операции для групповых кодов. Инвертирование разрядов кодовой комбинации, т.е замена ее комбинацией смежного класса, выполняется на выходе кодера, и обратная операция- на входе декодера.
В связи с этим важно оценить повлияет ли переход от кодовых комбинаций к комбинациям смежного класса в дискретном канале на помехоустойчивость кода.
Теория групповых кодов полностью определяет свойства смежно-групповых кодов. Легко показать, что корректирующие свойства смежно-групповых кодов не отличаются от корректирующих свойств групповых кодов, из которых они получены. Рассмотрим кодовое расстояние в смежно-групповом коде. 
и 
- две произвольные комбинации смежно-группового кода с образующим с. Тогда каждая из этих комбинаций может быть представлена через комбинацию исходного группового кода:
. Их сумма: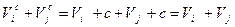 
равна комбинации исходного группового кода. Следовательно, расстояние между двумя любыми комбинациями смежно-группового кода определяется весом одной их кодовых комбинаций исходного группового кода.Итак, справедлива теорема:
Теорема 5.2. Кодовые расстояния смежно-группового кода совпадают с кодовыми расстояниями исходного группового кода. Это означает, что помехоустойчивость смежно-групповых кодов эквивалента помехоустойчивости исходных групповых кодов.
Задачи
1. Показать, что условие существования совершенных кодов задается границей Хэмминга.
2. Какие из перечисленных кодов, удовлетворяют условию совершенных
а)(23,12)-код, dmin=7,
б)(17,9)-код,dmin=7,
в)(63,57)-код,dmin=3,
г)(63,51)-код,dmin=5,
д)(7,4)-код,dmin=3.
3. Чему равно минимальное кодовое расстояние для (7, 4) – кода с проверочной матрицей
.
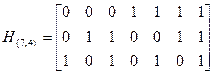4. Проверить, принадлежат ли комбинации
0 1 1 0 0 1 0 и 1 0 0 1 1 0 1 к одному смежному классу (7, 4) – кода.
5.Оценить выигрыш по достоверности, обеспечиваемой (7, 4) – кодом, с dmin =3 по сравнению с простым семиэлементным кодом при исправлении и при обнаружении ошибок в канале с группирующими ошибками.
Дата добавления: 2015-08-02; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оценка эффективности групповых кодов | | | Коды с единственной проверкой на четность |