Основные алгебраические системы, используемые в теории кодирования

Современные и перспективные помехоустойчивые коды строятся на основе некоторой математической модели, что позволяет достаточно просто решать вопросы определения их свойств и реализуемости. При построении кодов используются алгебраические системы: группа, векторное пространство, кольцо и поле.

а) Группа

Пусть имеется множество G элементов произвольной природы, которые обозначим a, b, c…, и пусть над этими элементами можно производить операцию сложения или умножения таким образом, что двум любым элементам множества G по определенным правилам ставится в однозначное соответствие некоторый элемент того же множества G. В общем виде введенную операцию будем обозначать знаком 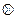. Для операции сложения и умножения будем использовать общепринятые знаки (“+” и ” ” соответственно).

Множество G называют группой, если для введенной операции оно удовлетворяет следующим требованиям:

G1. Множество замкнуто: если a и b принадлежат G, то и c, полученное на основе введенной операции также принадлежит этому же множеству элементов G. При сложении 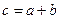, при умножении .

G2. Выполняется сочетательный (ассоциативный) закон:

.

При сложении ,

При умножении .

G3. Наличие единичного элемента e: среди элементов множества G имеется такой элемент e, для которого справедливо 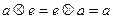, где a - произвольный элемент G.

В случае операции сложения над числами равенство возможно лишь в том случае, когда e = 0. Если же над числами производится операция умножения, то равенство возможно лишь в том случае, когда e = 1.

G4. Наличие обратных элементов: для произвольного элемента а множества G существует в этом множестве такой элемент 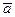, для которого справедливо

.

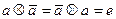Если элементами множества G являются числа, то при сложении , а при умножении .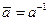

Примеры групп:

1. Множество целых чисел положительных, отрицательных и нуля является группой по операции сложения.

2. Числа 0 и 1 образуют группу по операции “сложение по модулю 2”.

1) Замкнутость. Обусловлена таблицей сложения

+

2) Сочетательность. Легко проверить, что сложение по модулю 2 подчиняется сочетательному закону, например

,

.

3) Единичный элемент. Здесь 0 является единичным элементом

4) Обратные элементы. Каждое число является обратным к самому себе, т.к. и .

Пример 5.1. Проверить, является ли множество трехразрядных комбинаций 000,001, 010 и 011 группой по операции поразрядного сложения по модулю 2.

1) Замкнутость. Составим таблицу сложения:

+

Мы видим, что сумма любой пары комбинаций также является комбинацией из данного множества, т.е. требование замкнутости удовлетворяется.

2) Сочетательность. Это требование также удовлетворяется, т.к. в основе операции – сложение по модулю 2.

3) Единичный элемент. Комбинация 000 является единичным элементом в данном множестве (см. таблицу сложения).

4) Обратные элементы. Обратной комбинацией для любой комбинации является эта же комбинация (см. таблицу сложения).

Итак, множество комбинаций 000, 001, 010 и 011 является группой по операции поразрядного сложения по модулю 2.

Группа называется абелевой в честь известного норвежского математика Н.Х. Абеля (1802-1829), если множество G по введенной операции обладает еще и следующими свойствами: , т.е. выполняется переместительный (коммутативный) закон. Группы, рассмотренные в предыдущих примерах, являются абелевыми.

Важным понятием в теории групп является понятие подгруппы.

Если множество элементов 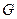составляет группу и некоторая часть этого множества (Н) также обладает всеми групповыми свойствами, то эту часть элементов группы называют подгруппой. Слово “подгруппа” означает “группа внутри группы”. Для того, чтобы установить, является ли Н подгруппой 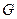необходимо проверить замкнутость и наличие обратных элементов. Если множество Н замкнуто относительно заданной в группе операций и содержит обратные элементы, то это множество содержит и единичный элемент группы, а сочетательный закон выполняется, так как он справедлив для всех элементов группы.

Основные свойства группы:

1. Группа содержит единственный единичный элемент, и для каждого элемента группы имеется единственный обратный элемент.

2. Группа разлагается на смежные классы по подгруппе. Смысл этого разложения заключается в следующем.

Обозначим элемент группы 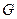через 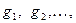а элемент подгруппы Н – через Рассмотрим таблицу, образованную следующим образом.

Запишем все элементы подгруппы Н, начиная с единичного элемента, в первую строку, причем каждый элемент подгруппы появится в этой строке только один раз. Далее выбираем любой элемент 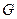, не принадлежащий Н, и записываем его на первое место во второй строке, а все остальные элементы второй строки находятся применением заданной в группе операции над первым элементом второй строки и соответствующими элементами подгруппы H, записанными в первой строке. Аналогично образуются третья, четвертая и т.д. строки, до тех пор, пока все элементы 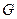не войдут в таблицу. В качестве первого элемента каждой строки всякий раз выбирается произвольный элемент 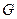, не вошедший в предшествующие строки. Этот элемент называют образующим смежного класса.

В результате получаем таблицу следующего вида:

Строки полученной подобным образом таблицы называются смежными классами.

Основные свойства разложения группы на смежные классы по подгруппе формулируются следующим образом:

3. В таблице разложения группы 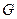на смежные классы по подгруппе Н перечисляются все элементы группы 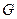, причем каждый элемент появляется в таблице только один раз.

4. Состав смежного класса постоянен и не зависит от выбора образующего элемента.

5. Число элементов в Н является делителем числа элементов в .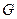

6. Два элемента g_i и g_j группы G принадлежит одному и тому смежному классу по подгруппе H тогда и только тогда, когда g_i 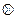g_j принадлежат H.

7. Операция, введенная над элементами группы, может быть введена и над смежными классами. Обозначим{ g_i } смежный класс, содержащий элемент группы {g_i}. Тогда {g_i} 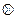{ g_j }={ g_i 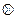g_j }, т.е. в результате операции над смежными классами, содержащими элементы g_i и g_j, получается новый смежный класс, содержащий g_i 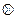g_j. В случае абелевой группы операция над смежными классами приводит к группе, элементами, которой является смежные классы.

Дата добавления: 2015-08-02