Принципы построения помехоустойчивых кодов

Одним из существенных процессов в аппаратуре передачи данных является кодирование и декодирование передаваемой информации, т.е. установление взаимно однозначного соответствия между ансамблем сообщений, вырабатываемых источником, и множеством кодовых комбинаций, используемых для передачи сообщений. Совокупность всех кодовых комбинаций, предназначенных для передачи по системе связи, принято называть кодом. Известно, что код характеризуется такими параметрами как основание, длина кодовой комбинации, число кодовых комбинаций. Основание кода b – это количество различных значений элементов, из которых формируются кодовые комбинации. Коды с основанием b = 2 получили название двоичных, с основанием b = 3 – троичных, с b = 4 – четверичных и т.д.

Длина кодовой комбинации (значность кода) равна количеству составляющих ее элементов n.

Если длина всех кодовых комбинаций одинакова, то код называется равномерным, в противном случае – неравномерным. В передаче данных нашли применение только равномерные коды. Равномерные коды составляют класс блоковых кодов, в которых каждому отдельному знаку сообщения сопоставляется кодовая комбинация (блок) из определенного числа элементарных символов(элементов).

Наряду с блоковыми кодами, существуют коды, в которых кодирование и декодирование представляют операции, производимые непрерывно над последовательностями символов, составляющих сообщение.

Деление передаваемой информации на блоки в этом случае отсутствует. Коды такого типа называются непрерывными.

Важным параметром кода является количество кодовых комбинаций, образующих код. Для равномерных блоковых кодов, каждая кодовая комбинация которых содержит n независимых переменных, имеющих b возможных значений, полное множество всех кодовых комбинаций равно

.

В реальной системе передачи данных действие различных помех приводит к искажению символов в принимаемом сообщении. Применение помехоустойчивых кодов – одно из эффективных современных методов борьбы с ошибками в принимаемых сообщениях.

Помехоустойчивыми (избыточными, корректирующими) называются коды, позволяющие обнаруживать и (или) исправлять ошибки, возникающие в сообщении в процессе передачи вследствие воздействия помех.

Поясним принцип построения таких кодов на примере двоичных кодов, значения символов которых обозначим 0 и 1.

Идея построения корректирующих кодов заключается в том, что для передачи сообщений источника информации используется не все полное множество возможных кодовых комбинаций, а лишь некоторая их часть.

(5.1)

Это выражение определяет условие построения помехоустойчивого кода.

Те N комбинации, которые составляют код, часто называют разрешенными, а те комбинации, которые не используются для передачи, - запрещенными.

Принцип обнаружения ошибок кодом состоит в следующем. Если в результате воздействия помех переданная кодовая комбинация переходит в запрещенную, то при анализе принятой комбинации в декодере источника это выявляется и тем самым устанавливается факт наличия ошибки в принятой комбинации. Ясно, что если под воздействием помех переданная комбинация трансформируется в разрешенную, то в этом случае ошибки не обнаруживаются и происходит ложное отождествление принятого сообщения с некоторым сообщением источника (необнаруженная ошибка). Таким образом, множество запрещенных комбинаций можно рассматривать как общую защитную область кода.

Итак, ошибки в переданной комбинации обнаруживаются в случаях возможных искажений, а всего код, удовлетворяющий условию (5.1.), способен обнаружить ошибки в 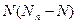случаях искажений сообщений источника.

Соответственно число необнаруживаемых искажений составляет величину . При этом доля обнаруживаемых искажений от всевозможных трансформаций сообщений источника равна , а необнаруживаемых - .

Аналогичным образом можно пояснить и принцип построения кода, исправляющего ошибки. Специфика состоит в том, что в этом случае недостаточно только выявить наличие ошибок в принятой кодовой комбинации, но и необходимо определить их местоположение, т.е. установить, какая кодовая комбинация была передана в действительности. Для этой цели необходимо создать их неиспользуемых комбинаций защитную зону для каждой кодовой комбинации, т.е. все множество запрещенных комбинаций разбить на непересекающихся подмножеств. При этом каждой кодовой комбинации приписывается вполне определенная защитная зона . Состав каждой защитной зоны определяется статистикой ошибок в канале связи. Процесс исправления ошибок заключается в том, что принятая запрещенная комбинация отождествляется с той разрешенной кодовой комбинацией, в зону которой данная запрещенная комбинация входит. Например, если передана подовая комбинация , и под воздействием помех в канале она трансформировалась в запрещенную комбинацию , принадлежащую зоне , то декодер источника выдаст получателю комбинацию .

Если же переданная комбинация трансформируется в некоторую другую разрешенную комбинацию или любую комбинацию, принадлежащую ее защитной зоне , то декодер источника отождествляет переданную комбинацию с комбинацией , что приводит к появлению ошибки в сообщении, доставляемом получателю. На рисунке 5.1. иллюстрируются указанные переходы, причем e_i и e_j – это векторы ошибок, накладываемые на кодовую комбинацию .

Рис 5.1 Процедура декодирования при исправлении ошибок

Следовательно, чтобы с большей вероятностью исключить возможность ложного отождествления принятых комбинаций с другими разрешенными, необходимо для каждой кодовой комбинации предусмотреть защитную зону, содержащую все наиболее вероятные трансформации данной комбинации. Очевидно, что чем большее число наиболее вероятных трансформаций включает защитная зона, тем выше корректирующие свойства кода. Декодирование, осуществляемое по данному методу, получило название декодирования по методу максимального правдоподобия.

У наиболее эффективных помехоустойчивых кодов число разрешенных комбинаций значительно меньше по сравнению с полным числом возможных комбинаций. При этом код способен исправить возможных искажений кодовых комбинаций.

В этом отношении обнаружение ошибок эффективнее, чем исправление. На рис. 5.2 иллюстрируются возможные трансформации и исходы при использовании кода, содержащего две разрешенные комбинации 000 и 111 в режиме обнаружения (а) и исправления (б).

Дата добавления: 2015-08-02