Основные характеристики помехоустойчивых кодов

Избыточность кода. Выше показано, что корректирующие свойства кода определены условием . Длина кодовой комбинации может быть определена, как . Для того, чтобы создать N различных комбинаций, достаточно иметь число двоичных независимых переменных, равных 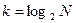. Итак, в каждую кодовую комбинацию помехоустойчивого кода введено 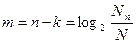дополнительных символов, для того, чтобы получить запрещенных комбинаций.

Установление однозначного соответствия между к – элементными комбинациями простого кода и n – элементными комбинациями корректирующего кода и составляет процесс кодирования. Эта операция осуществляется в кодере передатчика устройства защиты от ошибок (УЗО).

Таким образом, в каждой кодовой комбинации помехоустойчивого кода, наряду с k символами, несущими информацию источника сообщений (информационные символы), имеется m символов, обеспечивающих коду корректирующие свойства (избыточные символы). Если местоположение информационных и избыточных символов в кодовой комбинации известно, то код принято называть разделимым. В противном случае код называют неразделимым.

Вводимая в кодовую комбинацию избыточность оценивается либо числом избыточных символов m (абсолютная избыточность), либо отношением 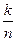(скорость или коэффициент передачи кода).

Под весом кодовой комбинации двоичного кода принято понимать количество элементов со значением “I” в данной комбинации. В качестве меры удаленности одной кодовой комбинации от другой используют кодовое расстояние (расстояние Хэмминга).

Кодовое расстояние между двумя комбинациями определяется числом символом, в которых эти комбинации отличаются. Кодовое расстояние принято обозначать буквой d. Для двоичных кодов расстояние между двумя комбинациями, например и , можно определять как вес результата поразрядного сложения элементов этих комбинаций по модулю 2:

.

Минимальное кодовое расстояние (d_min) между различными парами кодовых комбинаций может быть использовано для оценки корректирующих свойств кода, предназначенного для обнаружения или исправления многократных ошибок.

Пусть s означает кратность (число) гарантийно обнаруживаемых кодом ошибок, а t есть кратность гарантийно исправляемых ошибок. Если код используется только для обнаружения ошибок, то для того, чтобы обнаружить все варианты из s или менее ошибок в кодовой комбинации, необходимои достаточно иметь минимальное кодовое расстояние равным .

Действительно, если минимальное расстояние равно s+1 (рис. 5.3а), то никакой вариант S – кратной ошибки не может перевести передаваемую комбинацию в разрешенную, в то время как при минимальном расстоянии , существует хотя бы одна пара комбинаций, отстоящих друг от друга на расстоянии меньшем или равном, s и найдется такой вариант s - кратной ошибки, который трансформирует одну из этих комбинаций в другую.

Аналогично исправление всех t и менее кратных ошибок возможно тогда и только тогда, если 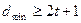. В этом случае в защитную зону каждой кодовой комбинации входят все запрещенные комбинации, отличающиеся от нее в 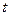символах и менее (рис. 5.3б). Любая комбинация с ошибками отличается от переданной в символах, а от другой кодовой комбинации в символах потому будет отождествлена декодером приемника УЗО с переданной комбинацией. Если же , то возможен хотя бы один случай, когда ошибка кратности t трансформирует переданную комбинацию в такую запрещенную комбинацию, которая столь же близка к одной из непередававшихся разрешенных комбинаций, как и к переданной.

Аналогичными рассуждениями можно показать, что для одновременного исправления всех ошибок кратности до включительно и обнаружения всех ошибок кратности до 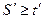, необходимо и достаточно, чтобы выполнялось условие 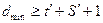(рис.5.3в).

а) Минимальное кодовое расстояние для кода, гарантийно обнаруживающего S-кратные ошибки

б) Минимальное кодовое расстояние для кода, гарантийно исправляющего t-кратные ошибки

в) Минимальное кодовое расстояние для кода, гарантийно обнаруживающего ошибки кратности до S' и исправляющего V кратные ошибки

Рис 5.3

Дата добавления: 2015-08-02