Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Необходимость поэлементной синхронизации . Расчет времени удержания синхронизма.

Распределение дроблений | Расчет вероятности ошибки при краевых искажениях | Расчет вероятности ошибки при дроблениях | Пример. | Поток ошибок в дискретном канале | Методы выявления и исследования последовательностей ошибок | A. Характер распределения ошибок в реальных каналах | Математические модели дискретных каналов с группированием ошибок | А. Модель неоднородного канала. | В.Корреляционные свойства модели Л.П. Пуртова |


Читайте также:
  1. I. Выбор электродвигателя и кинематический расчет привода.
  2. I. Кинематический расчет привода.
  3. II г. Основные расчетные соотношения.
  4. II) Найдитев тексте и выпишитев две колонки: наречия времении наречия места.
  5. II. Проектировочный расчет червячной передачи.
  6. III. Расчет по I группе предельных состояний.
  7. III. Расчет фермы покрытия.

Пусть fзг – частота задающего генератора.Отклонение частоты от номинального значения через некоторое время работы с учетом всех дестабилизирующих факторов составит

∆ f = fзг - f1.

Определим К = ∆ f / fзг - коэффициент нестабильности задающего генератора.

 

Нас интересует время, в течение которого фаза управляющих импульсов приемника разойдется с фазой управляющих импульсов передатчика. Находим

tп = 1/ ∆ f = 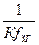- за это времяфаза разойдется на 1 период колебания Т.

 

. Определим время, в течение которого фаза разойдется на значение t0 :

 

tt = = = ,

где

- скорость передачи единичных элементов,

K- коэффициент нестабильности задающего генератора.

 

Уход на t0 – сохранение синхронизации. Интересует уход фазы на εt0- часть от t0:

tεt = .

Двойка в знаменателе учитывает нестабильность обоих задающих генераторов взаимодействующих комплектов АПД.

Задача: Определить время,в течение которого система связи выйдет из синхронизма, если скорость передачи единичных элементов Re=64 кбит/с, а коэффициент нестабильности задающего генератора К = 10-6. Выходу из синхронизма соответствует значение ε =0,5.

Вычисляем tεt = :

t0,5t = =

Таким образом, условию задачи соответствует выход из синхронизма примерно через 4 секунды.

 

Дата добавления: 2015-08-02; просмотров: 88 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Требования к УСП| Схема ФАПЧ с дискретным управлением.
mybiblioteka.su - 2015-2024 год. (0.006 сек.)