В.Корреляционные свойства модели Л.П. Пуртова

Установим связь между показателем группирования ошибок α и корреляционными характеристиками последовательности ошибок в дискретном канале. Для установления этой связи рассмотрим корреляционную зависимость между двумя соседними искаженными блоками длины n.

Пусть событие А есть появление искаженного блока n в процессе передачи сообщений; соответствующая этому событию вероятность P(A)=P(1). Событие В состоит в появлении ошибок в последующем блоке длины n; вероятность этого события есть Р(В)=Р(1).

Вероятность появления двух подряд искаженных блоков обозначим Р (А В) = Р (1,1).

Известно, что коэффициент корреляции между двумя искаженными блоками можно вычислить по формуле:

R=

Подставляя в это выражение необходимые вероятности, получим:

R₁₁=R=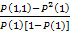

Таким образом, задача сводится к вычислению Р(1) и Р(1,1) при помощи модели Л.П.Пуртова.

Заметим, что:

Р(0,0)+Р(0,1)+Р(1,0)+Р(1,1)=1, где

Р(0,0) — вероятность появления двух неискаженных блоков;

Р(1,0)=Р(0,1) — вероятность появления только одного искаженного блока из двух, идущих подряд.

Подставляя значение для Р(1,1) в выражение для R, получим:

R=

Преобразуем:

P(0,1)=P(0)-P(0,0)

Окончательно получим:

R=

Учитывая, что в соответствии с моделью Л.П.Пуртова:

Р(1)=n^{1- α}p

Р(0)=1- n^{1- α}p

Р(0,0)=1-(2n)^{1- α}p,

после преобразования имеем:

Эта формула устанавливает связь между четырьмя величинами n, p, α, R, характеризующими дискретный канал связи при блочной передаче сообщений.

Положив n=1, получим связь вероятности ошибки символа p, показателя группирования α и коэффициента корреляции между двумя соседними ошибками r:

2^{1- α} = (2 - p) - r (1 - p),

откуда

α = 1 - log₂ [1 + (1 - r)(1 - p)].

В реальном канале p<<1, а корреляция r между ошибками существенная, в связи с чем полученное выражение может быть упрощено:

α ≈ 1 - log₂(2 - r).

С учетом возможных значений r в реальных каналах (0 ≤ r ≤ 1), находим подтверждение принятых значений α:

0 ≤ α ≤ 1.

Установленная связь показывает, что показатель группирования ошибок α может быть вычислен не только на основе статистических данных по искажению кодовых комбинаций В_ош и числу ошибок М_ош, как это было показано выше, но и на основе измерения коэффициента корреляции между ошибками

Дата добавления: 2015-08-02