Пример 5.2.

Пусть G - группа по операции сложения (т.е. аддитивная группа), состоящая из всех положительных и отрицательных целых чисел и нуля, и пусть H – подгруппа, состоящая из всех чисел, кратных целому числу n. Все числа от нуля до n -1 принадлежат различным смежным классам, т.к. для того, чтобы a и b принадлежали одному смежному классу необходимо, чтобы число (-a)+b принадлежало подгруппе, т.е. было кратно n, что невозможно. Значит, числа от 0 до n -1 могут быть выбраны в качестве образующих смежных классов и других чисел, быть не может. Легко проверить, что группа G - абелева, поэтому можно ввести операцию сложения смежных классов и смежные классы образуют группу. Положим n=2. Тогда смежные классы имеют вид:

0, 2, -2, 4, -4, 6, -6,…

1, 3, -1, 5, -3, 7, -5,…

Если обозначить смежные классы {0}и {1} соответственно, то таблица сложения смежных классов получит вид:

+	{0}	{1}
{0}	{0}	{1}
{1}	{1}	{0}

В этой таблице легко узнается таблица сложения чисел по модулю 2.

б) Векторное пространство.

Множество элементов произвольной природы V, называемых далее векторами, образует векторное пространство, если оно удовлетворяет следующим требованиям.

1. Множество векторов образует абелеву группу по операции сложения векторов.

2. Определено правило умножения вектора 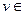V на скаляр с, где с в рассматриваемом нами случае принимает значение 0 или 1, и произведение 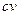является вектором того же векторного пространства V.

3. Выполняется распределительный закон:

- если с и d скаляры, а v - вектор (v 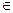V), то ,

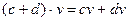- если v и u – векторы (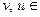 V), а с – скаляр, то .

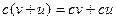4. Операция умножения на скаляр подчиняется сочетательному закону: если с, d – скаляры, а v - вектор (v 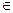V), то .

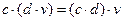Пример 5.3. Проверить, является ли набор комбинаций 000,001,010 и 011 векторным пространством.

В примере 5.1. было показано, что эти комбинации образуют группу по операции поразрядного сложения по модулю 2. Так как для любых комбинаций порядок сложения несущественен, например,001+010=010+001=011, то эта группа является абелевой.

Будем полагать каждую комбинацию вектором и умножение на скаляр производить следующим образом: 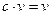, если с = 1, и 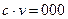, если с = 0, где v - любая из рассматриваемых комбинаций.

При таком введении операции умножения на скаляр выполняются распределительные законы, например:

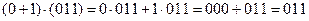и

1∙(011+010)= .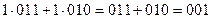

Операция умножения на скаляр подчиняется сочетательному закону, например,

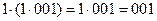, равно как .

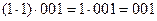Таким образом, набор комбинаций 000, 001, 010 и 011 при введении операций указанным выше способом удовлетворяет требованиям векторного пространства.

Рассмотренный пример показывает, что для двоичного случая свойства векторного пространства в основном определены свойствами абелевой группы.

Сформулируем некоторые понятия и определения, относящиеся к векторному пространству.

1) Сложение векторов

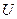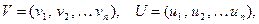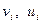Пусть V и - два вектора n – мерного векторного пространства где - скаляры (двоичные элементы). Тогда суммой этих векторов будем называть новый вектор 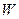, образованный по следующему правилу:

.

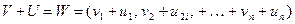2) Умножение вектора на скаляр

Пусть 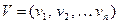вектор, а с – скаляр. Умножение вектора на скаляр дает новые вектор, образованный по следующему правилу:

.

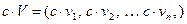3) Скалярное произведение векторов

Пусть V и U векторы: 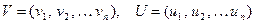. Скалярным произведением векторов называется скаляр (двоичный элемент), образованный по следующему правилу:

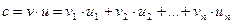
Знак “+”здесь имеет смысл сложения по модулю 2.

Если скалярное произведение векторов равно 0, то такие векторы называются ортогональными.

4) Линейная комбинация векторов

Линейной комбинацией векторов 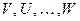называют вектор 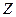, образованный по следующему правилу:

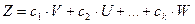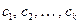, где - скаляры (двоичные элементы).

5) Линейная зависимость векторов

Если 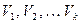есть векторы, 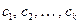есть скаляры, причем хотя бы один из них не равен0, то указанный набор векторов называется линейно-зависимым, если

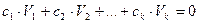
В этом случае, когда эта сумма обращается в 0 (чисто нулевой вектор 00…0) только лишь при равенстве всех скаляров нулю, этот набор векторов называют линейно-независимым.

6) Базис векторного пространства

Векторное пространство размерности n (n – мерное векторное пространство) со значением скаляров 0 или 1 содержит в своем составе 2 ⁿ различных векторов.

Это пространство может быть охарактеризовано базисом, состоящим из n линейно независимых векторов. Все остальные векторы можно получить путем линейных комбинаций базисных векторов.

Подпространство n – мерного векторного пространства размерности k, где k<n, содержит 2 ^k различных векторов, выбранных на 2 ⁿ векторов, составляющих n – мерное пространство, таким образом, что удовлетворяются все требования векторного пространства. Любой набор из k линейно-независимых векторов данного пространства может служить его базисом.

Пример 5.4. Набор векторов 000, 001, 010, 011, 100, 101, 110, 111 образует 3-мерное векторное пространство (2³ векторов). Его базисом могут служить следующие тройки векторов:

001, 010, 100 или 010, 011, 110 и т.д.

С помощью базисных векторов можно получить любой другой вектор данного 3-мерного пространства. Используя линейную комбинацию базисных векторов

,

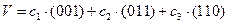получим, например, вектор101. Для этого надо взять 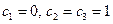, тогда

.

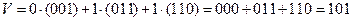Подбором 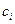можно получить каждый вектор рассматриваемого пространства.

В примере 5.3. мы установили, что набор векторов 000, 001, 010 и 011 удовлетворяет всем требованиям векторного пространства.

По отношению к полному набору векторов 3-мерного векторного пространства данный набор векторов является подпространством размерности 2.

Его базисы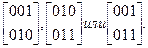

Дата добавления: 2015-08-02