Читайте также:
|
Широкое применение в теории кодирования нашло представление кодовых комбинаций в виде векторов некоторого векторного пространства или многочленов от формальной неизвестной х. Для двоичных кодов такое соответствие устанавливается следующим образом:
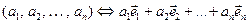, или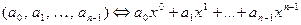 
,
где аi – элемент кодовой комбинации;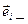 
opm n- мерноговекторного пространства; х – формальная переменная.
Таким образом, множество кодовых комбинаций n – элементного кода можно представить либо совокупностью векторов n -мерного векторного пространства, либо совокупностью многочленов, степень которых не старше n – 1. Такое представление дает возможность ввести действия над кодовыми комбинациями, аналогичные действиям над векторами или многочленами и использовать для построения корректирующих кодов алгебраические системы, описанные выше. Так, например, по аналогии с операциями над векторами n – мерного векторного пространства определим правило сложения двух n – элементных кодовых комбинаций следующим образом:
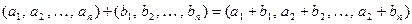
В этом случае, когда элементами кодовой комбинации являются двоичные элементы 0 и 1, то результирующая кодовая комбинация получается путем поразрядного сложения по модулю 2 исходных комбинаций.
Умножение кодовой комбинации на скаляр (двоичный элемент) определим правилом
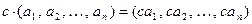
Под скалярным произведением двух кодовых комбинаций длины n будем понимать скаляр (двоичный элемент), получаемый следующим образом:
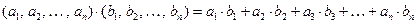
Если скалярное произведение двух кодовых комбинаций равно 0, то такие кодовые комбинации будем называть ортогональными.
Дата добавления: 2015-08-02; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 5.2. | | | Определение группового кода |