
На основе группового (n, k) – кода можно построить также групповой (n- i, k-i) – код, если в каждой кодовой комбинации (n, k) – кода исключить i информационных символов.
Порождающая матрица (n- i, k-i) – кода получается из канонической формы матрицы G(n, k) вычеркиванием i последних строк и i последних столбцов. Проверочная матрица (n- i, k-i) – кода получается из канонической формы Н(n,k) вычеркиванием i последних столбцов. Поскольку при этом число линейно зависимых столбцов матрицы проверок уменьшиться не может, то dmin нового кода и его корректирующие свойства не хуже, чем у исходного кода.
Коды, построенные таким образом, принято называть укороченными кодами.
Пример 5.11. Из известного кода (5, 3) получить код (4, 2).

Вычеркиваем из матрицы G(5,3) третью строку и пятый столбец, а из матрицы Н(5,3) пятый столбец. В результате получаем порождающую матрицу и матрицу проверок кода (4, 2):
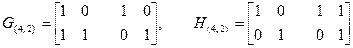 .
.
Минимальное число линейно независимых столбцов матрицы Н(4,2) по-прежнему равно 2. Следовательно, и dmin этого кода равно 2.
Дата добавления: 2015-08-02; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Б. Процедура декодирования | | | Оценка эффективности групповых кодов |