Оценка эффективности групповых кодов

В качестве оценки помехозащищенности помехоустойчивого кода используется вероятность ошибочного приема кодовой комбинации. Для расчета этой вероятности должны быть известны следующие характеристики кода и дискретного канала:

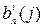- функция ошибок, принимающая значения 0 и 1 и указывающая

выявляется или не выявляется данным кодом конкретный j –тый образец i- кратной ошибки; j принимает значения чисел натурального ряда от 1 до 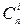; i изменяется от 1 до n.

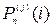- вероятность появления j -го образца i- кратной ошибки в дискретном канале; определяется либо в результате статистических испытаний, либо вычисляется аналитически, если известен характер распределения ошибок и математический закон их описания.

Вероятность ошибочного приема кодовой комбинации может быть определена как

.

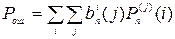Это – точная формула. Однако, в большинстве практических случаев расчеты по данной формуле затруднительны. В тех случаях, когда можно считать вероятности появления различных образцов ошибок кратности i достаточно близкими по значению, т.е.

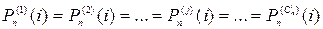
приведенная выше формула упрощается и принимает вид

,

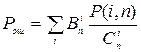где 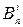- число вариантов, не выявляемых кодом ошибок кратности i. Очевидно, что

.

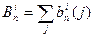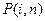-вероятность появления в дискретном канале ошибки кратности i.

.

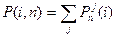Если известно, что данный помехоустойчивый код гарантийно выявляет (исправляет или обнаруживает в зависимости от режима использования кода) все ошибки кратности 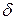и менее, то пределы суммирования можно уточнить

.

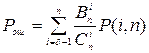Отношение 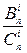можно рассматривать как долю невыявляемых ошибок кратности i от общего числа возможных ошибок этой кратности.

При использовании процесса декодирования, описанного в разделе 3.2, формула уточняется в соответствии с используемым режимом кода. Рассмотрим возможные режимы использования кода.

Одним из возможных режимов является исправление ошибок.

Ложное отождествление принятой комбинации с одной из разрешенных происходит в том случае, когда в комбинации имеет место ошибка, кратность которой превышает кратность гарантийно исправляемых ошибок и которая не вошла в число образующих смежных классов.

Пусть код гарантийно исправляет все ошибки кратности до t включительно. Вероятность появления в кодовой комбинации неисправляемых ошибок равна

.

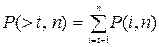Из общего числа 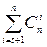возможных ошибок кратности большей, чем t, к ошибочному результату при декодировании с исправлением приводят те, под воздействием которых искаженные комбинации попадут в смежные классы, соответствующие исправляемым образцам ошибок. В предположении, что комбинации с ошибками кратности t+ 1 и выше равномерно распределяются по смежным классам таблицы декодирования, общая доля ошибочных исходов при исправлении ошибок кратности t+1 и выше составит величину

.

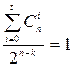Итак, вероятность ошибочного приема кодовой комбинации при исправлении ошибок равна

.

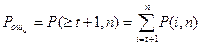Другой возможный режим – это обнаружение ошибок. Пусть код обнаруживает все варианты S – кратных ошибок и все ошибки меньшей кратности. В этом случае ошибка возможна лишь тогда, когда кодовая комбинация, искаженная ошибкой кратности большей S, трансформируется в разрешенную кодовую комбинацию, т.е. попадает в первую строку таблицы декодирования. Так как общее число строк в таблице декодирования равно 2 ^n-k, то доля исходов, приводящих к ошибке, в этом случае равна .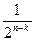

Другими словами, это же явление можно пояснить следующим образом. При оценке результата декодирования с помощью синдрома ошибка возможна лишь в том случае, когда кодовой комбинации, пораженной ошибками кратности большей S, соответствует чисто нулевой синдром (трансформация в разрешенную комбинацию). Если при поражении кодовой комбинации ошибками кратности большей S синдром не принимает чисто нулевое значение (трансформация в запрещенную комбинацию), то ошибки обнаруживаются.

При условии равномерного распределения кодовых комбинаций, пораженных ошибками кратности большей S, по возможным значениям синдрома имеем общее число возможных исходов равным 2 ^n-k, при числе исходов, приводящих к ошибке – равным 1. Итак, доля не обнаруживаемых искажений кодовой комбинации равна 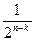. Данный результат уточняет значение доли необнаруживаемых ошибочных трансформаций, выведенной в разделе 5.1.2. на случай групповых кодов:

.

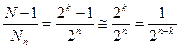Вероятность ошибочного приема в этом случае равна

.

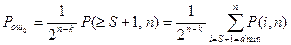Возможен такой режим декодирования, при котором часть ошибок исправляется, а часть обнаруживается. Пусть код имеет минимальное кодовое расстояние d_min. В том случае, когда этот код используется для исправления ошибок кратности 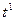и гарантийного обнаружения ошибок кратности до S=d-t'-1 включительно, вероятность ошибочного приема кодовой комбинации в дискретном приемнике равна

.

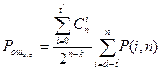
Полученные выше формулы можно использовать для расчетов, когда известна вероятность .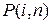

Приведем сводку расчетных формул для случая двоичного симметричного канала и канала с группированием ошибок (модель )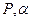

Режим декодирования	Вероятность ошибки	Двоичный симметричный канал	Модель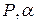
Исправление ошибок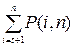
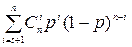
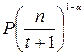
Обнаружение ошибок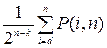
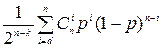
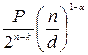
Частичное исправление и обнаружение ошибок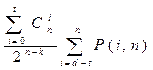

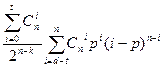
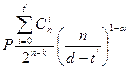
В этой таблице d=dmin.

Дата добавления: 2015-08-02