
Читайте также:
|
Любой циклический (n, k) – код может быть задан в соответствии с определением 2, порождающим многочленом g(x) или проверочным многочленом  .
.
Знание этих многочленов позволяет построить порождающую матрицу и матрицу проверок. Для циклического (n, k) – кода существует простой способ нахождения k линейно независимых кодовых комбинаций, образующих порождающую матрицу  . Этот способ состоит в следующем. Записывается порождающий многочлен g(x). В соответствии с определением 2 комбинация, соответствующая порождающему многочлену, принадлежит циклическому (n, k) – коду. В соответствии с определением 1 циклические сдвиги комбинации, соответствующей g(x), также должны принадлежать этому же коду. Алгебраически сдвиг соответствует умножению кодовой комбинации на х. Так как степень g(x) равна n-k, то подобным образом мы можем получить кодовые комбинации
. Этот способ состоит в следующем. Записывается порождающий многочлен g(x). В соответствии с определением 2 комбинация, соответствующая порождающему многочлену, принадлежит циклическому (n, k) – коду. В соответствии с определением 1 циклические сдвиги комбинации, соответствующей g(x), также должны принадлежать этому же коду. Алгебраически сдвиг соответствует умножению кодовой комбинации на х. Так как степень g(x) равна n-k, то подобным образом мы можем получить кодовые комбинации

Легко проверить, что эти кодовые комбинации линейно независимы, хотя бы потому, что степени всех этих многочленов различны, поэтому данный набор многочленов может быть использован в качестве  :
:
 .
.
Путем элементарных преобразований эта матрица может быть приведена к канонической форме.
Аналогичным образом по проверочному многочлену  можно построить матрицу проверок
можно построить матрицу проверок 
 .
.
Пример 6.4. Для циклического (7,4) – кода с порождающим многочленом  (см. пример 6.3.) построить порождающую матрицу.
(см. пример 6.3.) построить порождающую матрицу.
Находим




Следовательно, порождающая матрица для данного кода имеет вид:

Полученные результаты и рассуждения относительно алгебраической структуры циклических кодов, приведенные в разделе 6.2, позволяют подметить одно важное свойство циклических кодов, определенное их циклической структурой.
Свойство 6.1. Произведение кодовой комбинации циклического кода 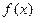 на произвольный многочлен
на произвольный многочлен  дает кодовую комбинацию этого же циклического кода.
дает кодовую комбинацию этого же циклического кода.
Действительно  , а любое произведение такого вида равно нулю, т.е. принадлежит кодовому подпространству (раздел 6.2).
, а любое произведение такого вида равно нулю, т.е. принадлежит кодовому подпространству (раздел 6.2).
Более элементарное доказательство:
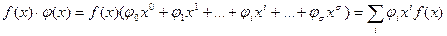 .
.
Полученная сумма есть сумма циклических сдвигов кодовых комбинаций, что по свойству замкнутости группового кода должно дать комбинацию того же циклического кода.
При описании циклических кодов следует учитывать специфику действий над многочленами, по сравнению с векторами и, в частности, тот факт, что умножение многочленов не совпадает со скалярным умножением векторов, отображающих эти многочлены. Однако в классе вычетов многочленов по модулю 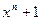 между этими понятиями существует весьма тесная связь. Пусть имеется вектор
между этими понятиями существует весьма тесная связь. Пусть имеется вектор  и соответствующий ему многочлен
и соответствующий ему многочлен  , а также вектор
, а также вектор  и соответствующий ему многочлен
и соответствующий ему многочлен  . Будем считать многочлены
. Будем считать многочлены  и
и  ортогональными, если выполнено условие
ортогональными, если выполнено условие  .
.
Коэффициент при х в произведении  равен
равен
 .
.
Слагаемые, содержащие  , появляются вследствие слагаемых в произведении
, появляются вследствие слагаемых в произведении  , которые содержат
, которые содержат  . Но так как
. Но так как  , т.е.
, т.е. 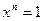 , то
, то  . Равенство для
. Равенство для  можно представить в виде скалярного произведения:
можно представить в виде скалярного произведения:
 .
.
В этом произведении первый вектор соответствует а(х). Второй вектор содержит коэффициенты b(х), расположенные в обратном порядке и сдвинутые циклически на j +1 элемент вправо.
Таким образом, если произведение  равно нулю, то вектор, соответствующий многочлену а(х), ортогонален вектору, соответствующему многочлену b(х), компоненты которого расположены в обратном порядке, и кроме того каждому циклическому сдвигу этого вектора. Верно также и обратное утверждение. Если вектор
равно нулю, то вектор, соответствующий многочлену а(х), ортогонален вектору, соответствующему многочлену b(х), компоненты которого расположены в обратном порядке, и кроме того каждому циклическому сдвигу этого вектора. Верно также и обратное утверждение. Если вектор  ортогонален вектору
ортогонален вектору  и каждому циклическому сдвигу этого вектора, то
и каждому циклическому сдвигу этого вектора, то
 .
.
Учитывая эту специфику необходимо при матричном описании кода коэффициенты матрицы проверок записывать в обратном порядке. В этом случае будет выполнено условие

Пример 6.5. Построить матрицу проверок для циклического (7,4) – кода из предыдущего примера.
Для построения матрицы проверок найдем проверочный многочлен

Отсюда
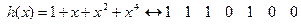


В силу того, что условие равенства нулю произведения многочленов и скалярного произведения соответствующих им векторов не совпадают, для выполнения равенства  при построении матрицы
при построении матрицы 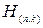 компоненты векторов, соответствующих h(x), xh(x) и x2h(x) записываем в обратном порядке
компоненты векторов, соответствующих h(x), xh(x) и x2h(x) записываем в обратном порядке
 .
.
В полученной матрице проверок в качестве столбцов записаны все 7 ненулевых последовательностей длины 3. Следовательно, данный код является кодом Хэмминга.
Вообще говоря, циклические коды Хэмминга строятся на основе порождающих многочленов степени m, являющихся сомножителями двучленов  и не являющихся сомножителями никаких двучленов меньшей степени. Корни этих многочленов имеют порядок 2m-1, т.е они являются примитивными элементами поля GF(2m). Это означает, что порождающий многочлен кода Хэмминга порождает поле GF(2m).
и не являющихся сомножителями никаких двучленов меньшей степени. Корни этих многочленов имеют порядок 2m-1, т.е они являются примитивными элементами поля GF(2m). Это означает, что порождающий многочлен кода Хэмминга порождает поле GF(2m).
Условимся в любом циклическом коде первые n-k элементов кодовой комбинации, то есть коэффициенты при  использовать в качестве проверочных элементов, а последние k элементов, то есть коэффициенты при
использовать в качестве проверочных элементов, а последние k элементов, то есть коэффициенты при 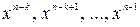 , - в качестве информационных (рис. 6.1).
, - в качестве информационных (рис. 6.1).
a0a, ….., an-1 = a0x0+a1x1+ …. + an-1xn+1
x0 x1 x2 xn-k-1 xn-k xn-2 xn-1
 a0 a0
| a1 | a2 | … … … ….. | an-k-1 |  an-k an-k
| … … … … | an-2 | an-1 |
Избыточные элементы Информационные элементы
Рис 6.1
Структура кодовой комбинации циклического кода
В этом случае в канонической форме порождающей матрицы  единичная матрица располагается справа. Такое расположение информационных и проверочных элементов обусловлено особенностями реализации кодирующих и декодирующих устройств циклических кодов.
единичная матрица располагается справа. Такое расположение информационных и проверочных элементов обусловлено особенностями реализации кодирующих и декодирующих устройств циклических кодов.
Всякий циклический (n, k) – код приводится к этой форме следующим образом.
Пусть  есть многочлен степени k -1, соответствующий комбинации простого k – элементного кода, которую необходимо закодировать циклическим (n, k) – кодом. В комбинации циклического (n, k) – кода эту k - элементную комбинацию необходимо поместить на позиции информационных элементов, для чего помножим многочлен
есть многочлен степени k -1, соответствующий комбинации простого k – элементного кода, которую необходимо закодировать циклическим (n, k) – кодом. В комбинации циклического (n, k) – кода эту k - элементную комбинацию необходимо поместить на позиции информационных элементов, для чего помножим многочлен  на
на  . В результате получаем многочлен
. В результате получаем многочлен  , степень которого равна n -1. Так как по определению циклического кода каждая кодовая комбинация должна делиться на порождающий многочлен g(x) степени n-k, то проверим выполнение этого условия. В общем случае в результате деления получим частное qi(x) степени k -1 и остаток, степень которого не превышает n-k -1. Результат деления представим в следующем виде:
, степень которого равна n -1. Так как по определению циклического кода каждая кодовая комбинация должна делиться на порождающий многочлен g(x) степени n-k, то проверим выполнение этого условия. В общем случае в результате деления получим частное qi(x) степени k -1 и остаток, степень которого не превышает n-k -1. Результат деления представим в следующем виде:
 .
.
Рассмотрим многочлен 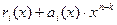 . Коэффициенты при
. Коэффициенты при  этого многочлена являются коэффициентами остатка
этого многочлена являются коэффициентами остатка 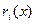 , а коэффициенты при степенях
, а коэффициенты при степенях 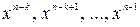 элементами первичной кодовой комбинации
элементами первичной кодовой комбинации  .
.
С другой стороны
 ,
,
то есть многочлен 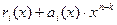 делится на g(x). Итак,
делится на g(x). Итак, 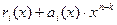 и есть искомая кодовая комбинация циклического (n, k) – кода. Отсюда получаем правило построения порождающей матрицы циклического (n, k) – кода в канонической форме:
и есть искомая кодовая комбинация циклического (n, k) – кода. Отсюда получаем правило построения порождающей матрицы циклического (n, k) – кода в канонической форме:
 ,
,
где Ik – единичная матрица размерности 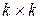 , соответствующая информационным элементам кодовых комбинаций,
, соответствующая информационным элементам кодовых комбинаций,  ;
;
 - матрица размерности
- матрица размерности  , j-я - строка, которой соответствует остатку от деления
, j-я - строка, которой соответствует остатку от деления  на g(x).
на g(x).
Матрица проверок 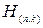 строится на основании матрицы
строится на основании матрицы  по правилу
по правилу
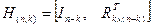 .
.
Пример 6.6. Построить порождающую матрицу и матрицу проверок в канонической форме для циклического (7,4) – кода с порождающим многочленом  . Находим частное и остаток от деления
. Находим частное и остаток от деления  на g(x) и записываем результат деления в форме равенства
на g(x) и записываем результат деления в форме равенства 
|
|


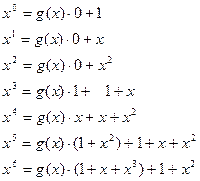
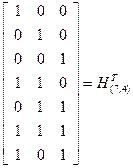
|
|


 .
.
Из рассмотренного примера видно, что проверочная матрица 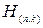 циклического (n, k) – кода содержит в качестве столбцов остатки от деления
циклического (n, k) – кода содержит в качестве столбцов остатки от деления  на порождающий многочлен g(x). Сравнение столбцов найденной проверочной матрицы с элементами поля GF(23) показывает их полное совпадение с ненулевыми элементами GF(23). Результаты рассмотренного примера будут использованы для обоснования эквивалентности различных столбцов вычисления синдрома.
на порождающий многочлен g(x). Сравнение столбцов найденной проверочной матрицы с элементами поля GF(23) показывает их полное совпадение с ненулевыми элементами GF(23). Результаты рассмотренного примера будут использованы для обоснования эквивалентности различных столбцов вычисления синдрома.
Дата добавления: 2015-08-02; просмотров: 157 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение циклического кода | | | Коды Боуза-Чоудхури-Хоквингема (БЧХ). |