Коды Боуза-Чоудхури-Хоквингема (БЧХ).

Определение корректирующих свойств циклических кодов, предназначенных для коррекции многократных ошибок, сводится к определению минимального кодового расстояния этих кодов или к установлению максимальных значений кратностей гарантийно исправляемых или обнаруживаемых ошибок.

Следующие две теоремы позволяют определить важнейший класс двоичных циклических кодов и установить корректирующую способность этого класса циклических кодов.

Теорема 6.1. Для любых значений l и t существует циклический код длины 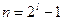, исправляющий все ошибки кратности t и менее и содержащий не более проверочных символов.

Формулировка этой теоремы заимствована из [1]. Следует уточнить, что при произвольном l параметр t не может быть любым. Его максимальное значение не должно превышать числа (n-1)/2, т.е. t≤2^r-l-1.

Пример 6. 7. Найти циклические коды длины n =31, исправляющие ошибки кратности t =1, 2, 3.

Определяем l. Так как 31=2⁵-1, то l =5. Находим количество проверочных элементов для заданных значений t:

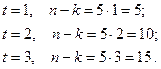
Таким образом, искомые коды (31, 26), (31, 21) и (31, 16).

Следует заметить, что теорема 6.1 определяет лишь существование кодов с известными корректирующими свойствами. Построение же кодов, действительно обладающих этими свойствами, зависит от правильного выбора порождающего многочлена.

Теорема 6.2. Если среди корней порождающего многочлена циклического (n, k) – кода имеются корни вида 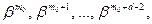то минимальное расстояние этого кода равно, по меньшей мере, d.

Циклические коды, удовлетворяющие этим теоремам получили название кодов Боуза-Чоудхури-Хоквингема, или кодов БЧХ по фамилиям их авторов.

Коды БЧХ - обширный класс кодов, предназначенный в первую очередь для исправления многократных ошибок. Коды БЧХ включают в свой состав коды Хэмминга и обобщают их на случай t>1.

Коды БЧХ существуют над полем GF(q), где q≥2. При этом Теорема 6.1., сформулированная для случая q=2, может быть обобщена для q>2. Однако, это обобщение выходит за рамки настоящего учебного пособия. Теорема 6.2. справедлива для q≥2 и будет использована при изучении недвоичных циклических кодов.

Изучение кодов БЧХ является основой для понимания других классов циклических кодов.

Дата добавления: 2015-08-02