Выбор порождающего многочлена для кода БЧХ

а) Порождающий многочлен для (n, n-1) – кодов.

В примере 6.3 было показано, что один из возможных кодов длины 7 есть (7,6) – код с 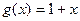. Покажем, что этот код образуется на основе проверки на четность всех информационных элементов кодовой комбинации. Для этого определим проверочный многочлен h(x) и построим проверочную матрицу (7,6) – кода. Находим

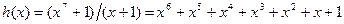и

,

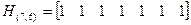т.е. действительно (7,6)-код с 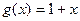является кодом с одной проверкой на четность по всем элементам кодовой комбинации. Распространим результат рассмотренного примера на общий случай.

В общем случае (n, n- 1) – кода при любом значении n проверочный многочлен находится как 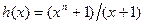. Так как двучлены 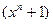и 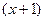имеют общий корень x =1, то справедливо

,

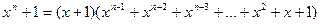т.е. многочлен 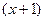порождает (n, n- 1) – код длины n с проверкой на четность по всем элементам.

б) Порождающий многочлен для общего случая циклического кода

Теорема 6.2 позволяет осуществить выбор порождающего многочлена для БЧХ кода и по его корням определить корректирующие свойства этого кода.

Пример 6.8. Порождающий многочлен кода (7,4) из примера 6.6 имеет своими корням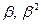и и 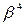. Определим корректирующие свойства этого кода.

Находим максимальное число последовательных степеней корней порождающего многочлена. Это элементы 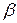и 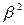. Здесь 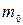=1, а 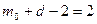, откуда d = 4- 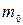= 3.

Использование теоремы 6.2 для выбора порождающих многочленов циклических кодов, а также для определения корректирующих свойств циклических кодов предполагает знание корней многочленов, которые могут быть выбраны в качестве порождающих многочленов кодов. Поскольку порождающий многочлен циклического (n, k) – кода должен быть делителем 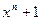, то для нахождения всех возможных кодов длины n, выбора порождающих многочленов и установления их корректирующих свойств необходимо знание сомножителей 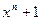и их корней.

Таблицы разложения 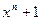с указанием корней неприводимых сомножителей в виде степеней 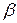и циклические коды, построенные на их основе, приведены в [2, 3].

Таблица кодов БЧХ с n=7÷1023 приведена в Приложении к настоящему пособию.

Пример 6.9. Найти порождающие многочлены для кодов длины n = 31 из примера 6.7. Из приложения 1 [2] находим неприводимые сомножители 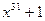и последовательности их корней:

Сомножитель	его степень	последовательность степеней корней
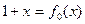
		0=31
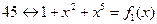
		1 2 4 8 16
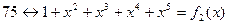
		3 6 12 24 17
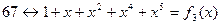
		5 10 20 9 18
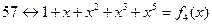
		7 14 28 25 19
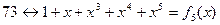
		11 22 13 26 21
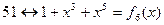
		15 30 29 27 23

Для кода (31,26) с t = 1 в качестве порождающего многочлена можно взять так как корни каждого из них содержат по две последовательные степени, а значит, по теореме 5.2 эти коды имеют d_min = 3.

Для кода (31,21) порождающий многочлен должен иметь степень 10. Он может быть получен, как произведение двух неприводимых многочленов пятой степени

В соответствии с теоремой необходимо, чтобы порождающий многочлен имел среди своих корней 4 последовательных степени. Этому требованию удовлетворяют, например, многочлены 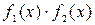и 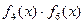. Для кода (31,16) в качестве порождающего многочлена целесообразно выбрать многочлены 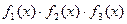и 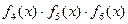, у которых среди корней имеются элементы 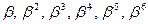и 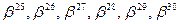соответственно, что обеспечивает требуемые корректирующие свойства кода.

в) Улучшение корректирующих свойств циклических (n, k) – кодов умножением порождающего многочлена на .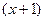

Для кодов с нечетным значением минимального кодового расстояния последнее может быть увеличено на единицу умножением порождающего многочлена g(x) на 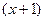. Выше было показано, что использование двучлена 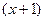в качестве порождающего многочлена дает код с проверкой на четность. Умножение порождающего многочлена некоторого циклического кода на 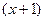приводит к введению дополнительной проверки на четность в этом коде по всем кодовым элементам. Если код имеет четное значение d_min, то дополнительная проверка на четность не изменит его величины, т.к. введение в проверочную матрицу строки из одних единиц не изменит минимального числа линейно не зависимых столбцов.

Если же d_min нечетное, то введение в проверочную матрицу строки из одних единиц приводит к увеличению минимального числа линейно зависимых столбцов на один.

Пример 6.10. Рассмотрим проверочную матрицу кода (7,3) из примера 6.3. Если в качестве порождающего многочлена выбрать 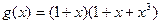, проверочным многочленом будет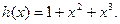

Матрица проверок для этого кода имеет вид

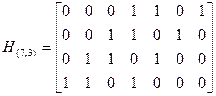
Сложив 1, 2 и 4-ю строки и записав результат вместо 4-й строки, получим проверочную матрицу этого же кода в следующем виде

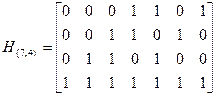
Проверочная матрица кода (6,3) с dmin=3 состоит из проверочной матрицы укороченного кода (7,4) (обозначена пунктиром), к которой добавлена строка, обеспечивающая проверку на четность по всем элементам кодовой комбинации. Минимальное кодовое расстояние равно 4 (линейно зависимы, например, 1, 2, 3 и 6-й столбцы).

г) Выбор порождающих многочленов для укороченных кодов

Как и все групповые коды, циклические коды могут подвергаться укорочению. При этом порождающий многочлен остается тем же, что и у исходного кода. Так как в результате укорочения уменьшается длина кодовой комбинации, то не все циклические сдвиги кодовой комбинации в укороченном (n - i, k - i) – коде будут кодовыми комбинациями. В силу этого обстоятельства, укороченные циклические коды называют псевдоциклическими. Методика построения кодовой комбинации для укороченного циклического кода остается той же, что была рассмотрена в разделе 6.2, т.е. каждая кодовая комбинация укороченного циклического кода кратна порождающему многочлену g(x), и корректирующие свойства укороченного циклического кода полностью определяются корнями g(x). Для укороченных кодов проверочные многочлены h(x) не определяются, а матрицы проверок строятся на основе порождающих матриц. Выбор порождающих многочленов для псевдоциклических кодов наиболее рационально производить на базе кодов, построенных по теореме 6.1. При этом можно при заданной абсолютной избыточности обеспечить требуемые корректирующие свойства и сохранить скорость передачи кода близкой к требуемой.

Пример 6.11. Выбрать порождающий многочлен для кода (50,35) с .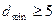

Выбор производим по необходимому числу избыточных элементов n - k =15. Так как требуется обеспечить 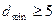, то по теореме 6.1 принимаем t =2. Ближайшее к требуемому значение избыточных элементов достигается при l =7.

Таким образом, исходным циклическим кодов является (127,113) – код с 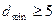. Этот код имеет 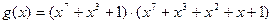. Следовательно, необходимо добавить еще один избыточный элемент. Для этого умножим g(x) на 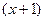, т.е. вводим проверку на четность по всем элементам. Получаем (127,112) – код с 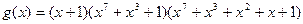. Укорочением данного кода на 77 разрядов получаем требуемый код. Итак, в качестве порождающего многочлена для кода (50,35) можно взять 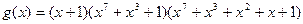. Данный код имеет .

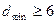Дата добавления: 2015-08-02