Эффективность двоичных кодов БЧХ

Для оценки эффективности кодов БЧХ воспользуемся теоремой 5.1, позволяющей установить соотношение между корректирующей способностью кода и его параметрами n и k.

Пусть для циклического (n, k) – кода справедливо для некоторого l, откуда .

Тогда кратность исправляемых ошибок этим кодов определяется как

.

Минимальное кодовое расстояние может быть найдено из известного соотношения

.

Этих сведений достаточно для краткого анализа эффективности циклического кода в реальном канале с известными параметрами р и α.

Для режима исправления ошибок выигрыш по достоверности по сравнению с простым кодом равен

.

Для режима обнаружения ошибок выигрыш составляет

.

Существенным является тот факт, что при исправлении ошибок теоретически возможно обеспечение любой степени повышения достоверности за счет увеличения длины кода n и числа избыточных элементов n - k. Однако практическая реализация таких кодов вызвала бы серьезные затруднения.

Рассмотрим пример.

Пример 6.12. Пусть некоторый реальный канал характеризуется параметрами

Найти циклический (n, k) – код, повышающий достоверность передачи на 1 десятичный порядок путем исправления ошибок, т.е. требуется найти код, для которого

Определим сначала необходимое количество избыточных элементов . Составим уравнение:

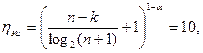
откуда

или

.

Потребное число избыточных элементов

.

Для нахождения кода с данным числом избыточных элементов составим таблицу

N

Из построенной таблицы видно, что требуемой эффективностью обладают коды с п >1000.

В частности, данной эффективностью обладают коды (1023, 10) и (1023,20), для которых эффективность равна

и

.

Сравнение значения для в режимах исправления и обнаружения позволяет сделать вывод, что режим обнаружения эффективнее исправления для одного и того же кода и канала в раз. Например, для кода (1023,10) из предыдущего примера эффективность при обнаружении ошибки равна .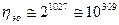

Задачи

1. Построить все циклические коды на основе разложения двучлена Ниже приведены сомножители и последовательности степени их корней.

Сомножитель Степени корней

x+1 0=15

x⁴+x+1 1 2 4 8

x⁴+x³ +x² +x+1 3 6 9 12

x²+x+1 5 10

x⁴+x³ [phone]

2. Определить корректирующие свойства циклического (15,11) – кода

а) с g(x)=1+x+x⁴;

б) с g(x)=1+x³+x⁴;

в) с g(x)=1+x+x²+x³+x⁴.

3. Определить корректирующие свойства циклического (15,7) – кода

а) с g(x)=(1+x+x⁴)(1+x³+x⁴);

б) с g(x)=(1+x+x⁴)(1+x+x²+x³+x⁴)

в) с g(x)=(1+x³+x⁴)(1+x+x+x²+x³+x⁴)

4. Построить порождающую матрицу и матрицу проверок для укороченного циклического (10,5) – кода, полученного из (15,10) – кода с g(x)=(1+x)(1+x+x⁴).

Определить d_min (10,5) – кода.

5. Привести матрицу проверок H(7,4),построенную в примере 6.5 к канонической форме.

6. Показать, что поле GF( 2³) с примитивным элементом α, являющимся корнем неприводимого многочлена π(x)= 1 +x+x³, может быть представлено в следующем виде:

Дата добавления: 2015-08-02