
Читайте также:
|
h(x) = h0 + h1x + … + hr-1xr-1 + hrxr
В этой схеме коэффициенты произведения формируются в регистре сдвига. После того, как по первому тактовому импульсу символ  поступил на вход, выход стал равным
поступил на вход, выход стал равным  , т.е. коэффициенту при
, т.е. коэффициенту при  , а в разрядах регистра записались элементы
, а в разрядах регистра записались элементы 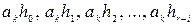 . По второму тактовому импульсу на вход подается
. По второму тактовому импульсу на вход подается  выход становится равным
выход становится равным  , т.е. коэффициенту при
, т.е. коэффициенту при 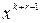 , а разряды регистра содержат элементы
, а разряды регистра содержат элементы  . По третьему тактовому импульсу на вход поступает
. По третьему тактовому импульсу на вход поступает 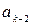 и выход равен
и выход равен  - коэффициенту при
- коэффициенту при  . Дальнейшие операции производятся аналогичным образом.
. Дальнейшие операции производятся аналогичным образом.
б) Схемы для деления многочленов.
Схема для деления многочлена произвольной степени п на многочлен  показана на рис.6.4. Схема представляет собою регистр сдвига с обратными связями. Обратные связи соответствуют виду многочлена g(x). В исходном состоянии ячейки регистра содержат нули. Делимый многочлен
показана на рис.6.4. Схема представляет собою регистр сдвига с обратными связями. Обратные связи соответствуют виду многочлена g(x). В исходном состоянии ячейки регистра содержат нули. Делимый многочлен  подается на вход схемы в течение (n+ 1) такта. Выход схемы деления в течение r первых тактов принимает значения, равные 0. Когда первый входной символ
подается на вход схемы в течение (n+ 1) такта. Выход схемы деления в течение r первых тактов принимает значения, равные 0. Когда первый входной символ  по (r+ 1)-му тактовому импульсу выйдет из регистра, то на выход схемы поступит старший коэффициент частного
по (r+ 1)-му тактовому импульсу выйдет из регистра, то на выход схемы поступит старший коэффициент частного 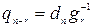 , который в рассматриваемом двоичном случае примет значение
, который в рассматриваемом двоичном случае примет значение  . При этом в последний разряд регистра будет записан символ
. При этом в последний разряд регистра будет записан символ 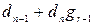 , в предпоследний
, в предпоследний  , и т.д., т.е. содержимое разрядов регистра будет соответствовать коэффициентам при степенях от
, и т.д., т.е. содержимое разрядов регистра будет соответствовать коэффициентам при степенях от  до
до  многочлена
многочлена  где суммирование осуществляется по модулю 2. Для каждого последующего (r+j)-го этапа деления содержимое разрядов регистра сдвига определяется коэффициентами при степенях от
где суммирование осуществляется по модулю 2. Для каждого последующего (r+j)-го этапа деления содержимое разрядов регистра сдвига определяется коэффициентами при степенях от  до
до  многочлена
многочлена  , где qi – символ, поступающий на выход схемы. После (n +1)-го такта работы схемы на выходе появится частное от деления q(x), а в ячейках регистра будет записан остаток от деления
, где qi – символ, поступающий на выход схемы. После (n +1)-го такта работы схемы на выходе появится частное от деления q(x), а в ячейках регистра будет записан остаток от деления  .
.
Пример 6.14. Построить схему для деления на многочлен  . Регистр должен содержать число ячеек, равное степени g(x), т.е. 3. Обратные связи должны соответствовать коэффициентам при xi:
. Регистр должен содержать число ячеек, равное степени g(x), т.е. 3. Обратные связи должны соответствовать коэффициентам при xi:
 .
.
Сумматор по модулю 2 включается на входе и в точке подключения обратной связи g 1. Схема, соответствующая рассматриваемому случаю представлена на рис. 6.5. На этом же рисунке показана работа схемы при делении многочлена 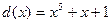 . В результате деления получено частное
. В результате деления получено частное 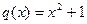 и остаток
и остаток  . Для того, чтобы установить соответствие между работой схемы и процессом деления многочлена d(x) на многочлен q(x) рассмотрим деление
. Для того, чтобы установить соответствие между работой схемы и процессом деления многочлена d(x) на многочлен q(x) рассмотрим деление  на
на  .
.


|

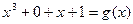
|




+
|
 0 0 0 0
0 0 0 0



|
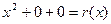
Остаток первого шага деления  содержится в разрядах регистра после выхода первого элемента частного к выходу схемы (4-й такт). Остаток второго шага деления
содержится в разрядах регистра после выхода первого элемента частного к выходу схемы (4-й такт). Остаток второго шага деления  содержится в разрядах регистра после вывода второго элемента частного к выходу схемы (5-й такт). Остаток от деления
содержится в разрядах регистра после вывода второго элемента частного к выходу схемы (5-й такт). Остаток от деления 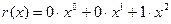 содержится в разрядах регистра после вывода последнего элемента частного (6-й такт).
содержится в разрядах регистра после вывода последнего элемента частного (6-й такт).

g0 +g1x+….+gn-k-1 xn-k-1+gn-kxn-k
| Такты | Вход | Содержимое регистра | Обратная связь | Выход | ||
| r0 | r1 | r2 | ||||
| - | 0 | 0 | 0 | 0 | - | |
| 0∙x5 | 1 | 0 | 0 | 0 | 0∙x6 | |
| 0∙x4 | 0 | 1 | 0 | 0 | 0∙x4 | |
| 0∙x3 | 0 | 0 | 1 | 0 | 0∙x3 | |
| 0∙x2 | 1 | 1 | 0 | 1 | 1∙x2 | |
| 1∙x1 | 1 | 1 | 1 | 0 | 0∙x1 | |
| 1∙x0 | 1∙x0 |
Остаток r(x)= x2
Работа схемы деления на многочлен g(x)=1+x+x3 при подаче на вход d(x)=1+x+x5
в) Схемы для одновременного умножения и деления многочленов
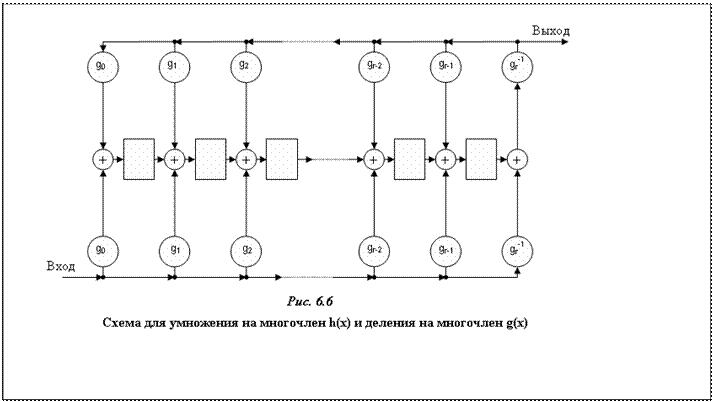 Схема, с помощью которой можно производить сначала умножение на многочлен h(x), а затем деление на многочлен g(x), изображена на рис. 6.6. Как видно из рисунка, она получена комбинированием схемы умножения, изображенной на рис 6.3 и схемы деления, изображенной на рис. 6.4. При построении схемы предполагается, что степень многочлена h(x) не превосходит степени g(x).
Схема, с помощью которой можно производить сначала умножение на многочлен h(x), а затем деление на многочлен g(x), изображена на рис. 6.6. Как видно из рисунка, она получена комбинированием схемы умножения, изображенной на рис 6.3 и схемы деления, изображенной на рис. 6.4. При построении схемы предполагается, что степень многочлена h(x) не превосходит степени g(x).
г) Схемы для решения рекуррентных соотношений
На рис. 6.7. изображена схема для решения рекуррентных соотношений вида  или, что то же самое
или, что то же самое  .
.

Эта схема предназначена для вычисления величины  по значению k предыдущих коэффициентов для всех возможных многочленов степени n -1, ортогональных некоторому многочлену h(x) степени k. Для циклического (n, k) – кода h(x) – проверочный многочлен кода. Исходные величины
по значению k предыдущих коэффициентов для всех возможных многочленов степени n -1, ортогональных некоторому многочлену h(x) степени k. Для циклического (n, k) – кода h(x) – проверочный многочлен кода. Исходные величины  помещаются в разряды регистра. Затем осуществляются последовательные сдвиги, каждый из которых сопровождается выводом с выхода схема элементов, соответствующих решению указанных рекуррентных уравнений. После первого сдвига на выход поступает элемент
помещаются в разряды регистра. Затем осуществляются последовательные сдвиги, каждый из которых сопровождается выводом с выхода схема элементов, соответствующих решению указанных рекуррентных уравнений. После первого сдвига на выход поступает элемент  , содержимое разрядов регистра сдвигается на одну единицу вправо, а в ячейку
, содержимое разрядов регистра сдвигается на одну единицу вправо, а в ячейку  поступит значение коэффициента
поступит значение коэффициента  , которое в соответствии со схемой рис. 6.7 должно быть равно сумме произведений коэффициентов, записанных во всех остальных разрядах регистра на значения обратных связей, подключенных непосредственно к выходам разрядов регистра, т.е.
, которое в соответствии со схемой рис. 6.7 должно быть равно сумме произведений коэффициентов, записанных во всех остальных разрядах регистра на значения обратных связей, подключенных непосредственно к выходам разрядов регистра, т.е.
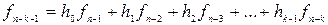 ,
,
что в точности соответствует значению  , полученному из рекуррентного соотношения.
, полученному из рекуррентного соотношения.
Аналогично можно показать формирование и всех остальных решений. В результате первых k сдвигов на выход схемы поступит содержимое разрядов регистра в исходном состоянии. Значение коэффициента  появится на выходе схемы в результате (k +1)-го сдвига, значение
появится на выходе схемы в результате (k +1)-го сдвига, значение  - в результате (k +2)-го сдвига и т.п. Поскольку для каждого значения исходных символов решение однозначно, то по последним k решениям сформируется и запишется в регистр
- в результате (k +2)-го сдвига и т.п. Поскольку для каждого значения исходных символов решение однозначно, то по последним k решениям сформируется и запишется в регистр  , затем
, затем  и т.д., т.е. схема будет генерировать решение рекуррентного уравнения непрерывно с периодом, равным n -1. Максимальное значение решений, т.е. максимальный период последовательности, можно определить из следующих соображений. Каждому решению соответствует свое вполне определенное значение разрядов регистра сдвига, следовательно, возможное число решений определяется числом различных состояний регистра. Так как каждая ячейка может характеризоваться двумя состояниями (запись нуля или единицы), а число ячеек в регистре равно k, то максимальное значение n равно 2k, а максимальный период последовательности равен 2k -1 и минимальный период равен k. В тех случаях, когда схема для решения рекуррентных соотношений генерирует последовательность с максимальным периодом, ее называют генератором последовательности максимальной длины. В силу того, что многочлен h(x) степени k, по которому стоится схема генератора последовательности максимальной длины, должен быть сомножителем двучлена
и т.д., т.е. схема будет генерировать решение рекуррентного уравнения непрерывно с периодом, равным n -1. Максимальное значение решений, т.е. максимальный период последовательности, можно определить из следующих соображений. Каждому решению соответствует свое вполне определенное значение разрядов регистра сдвига, следовательно, возможное число решений определяется числом различных состояний регистра. Так как каждая ячейка может характеризоваться двумя состояниями (запись нуля или единицы), а число ячеек в регистре равно k, то максимальное значение n равно 2k, а максимальный период последовательности равен 2k -1 и минимальный период равен k. В тех случаях, когда схема для решения рекуррентных соотношений генерирует последовательность с максимальным периодом, ее называют генератором последовательности максимальной длины. В силу того, что многочлен h(x) степени k, по которому стоится схема генератора последовательности максимальной длины, должен быть сомножителем двучлена  при
при 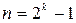 и не может быть сомножителем никакого двучлена с меньшим значением п (т.к. период равен 2 k -1), то h(x) должен быть неприводимым сомножителем
и не может быть сомножителем никакого двучлена с меньшим значением п (т.к. период равен 2 k -1), то h(x) должен быть неприводимым сомножителем  и не должен быть сомножителем двучленов меньших степеней, т.е. должен принадлежать показателю п. Поскольку последовательности максимальной длины соответствует 2k -1 различных состояний регистра сдвига (все возможные векторы длины k, кроме чисто нулевого), то для генерирования последовательности максимальной длины в качестве исходного состояния может быть взято любое, кроме чисто нулевого. Обычно для этой цели в младший разряд регистра предварительно записывают “1”. Некоторые из неприводимых многочленов, по виду которых строятся обратные связи в регистре, приводятся в таблице 6.3 для п =2+15.
и не должен быть сомножителем двучленов меньших степеней, т.е. должен принадлежать показателю п. Поскольку последовательности максимальной длины соответствует 2k -1 различных состояний регистра сдвига (все возможные векторы длины k, кроме чисто нулевого), то для генерирования последовательности максимальной длины в качестве исходного состояния может быть взято любое, кроме чисто нулевого. Обычно для этой цели в младший разряд регистра предварительно записывают “1”. Некоторые из неприводимых многочленов, по виду которых строятся обратные связи в регистре, приводятся в таблице 6.3 для п =2+15.
Таблица 6.3
| Число ячеек регистра | Неприводимый Многочлен | Вид обратной связи | Длина периода |

| 
| ||

| 
| ||

| 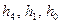
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 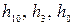
| ||

| 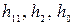
| ||

| 
| ||
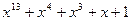
| 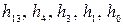
| ||

| 
| ||

| 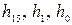
|
Для примера на рис.6.8 приведена структурная схема генератора последовательности максимальной длины, построенной на основе  .
.
Число ячеек регистра сдвига равно степени h(x), т.е шести. Число сумматоров по модулю 2 на единицу меньше числа знаков “+” в записи многочлена h(x), т.е. один. Обратные связи определяются ненулевыми коэффициентами многочлена 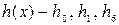

д) Схема генератора поля Галуа GF(2m)
Регистр сдвига с обратными связями, изображенный на рис. 6.4, реализующий деление любого многочлена на многочлен g(x) степени n-k=m, после завершения деления содержит остаток от деления
r(x) = r0x0+r1x1+r2x2+…+rm-1x0m-1.
Он может быть представлен в виде последовательности длины m-(r0, r1, r2,..,rm-1)
Многочлен r(x) является представителем классов вычетов многочленов по модулю многочлена g(x). При этом каждый класс вычетов содержит либо 0, либо многочлен степени m-1 и менее. Ноль является элементом идеала, а все многочлены r(x) степени m-1 и менее принадлежат различным классам вычетов. Общее число классов вычетов вместе с идеалом равно 2m.
В том случае, когда многочлен g(x) – неприводим, множество {r(x)} с коэффициентами ri из поля GF(2) образует поле Галуа GF(2m). Как известно ненулевые элементы этого поля образуют циклическую группу
α0, α1,…,α2m-2,α2m-1=α0,
где α -класс вычетов, содержащий r(x) = x, т.е. корень g(x) и примитивный элемент поля.
Определим, каким образом можно преобразовать схему рис 6.4 в генератор элементов поля GF(2m). В схеме деления на g(x) каждый из остатков r(x) может быть получен в результате подачи xi на вход схемы и осуществления процедуры деления в течение i тактов, т.е. остаток от деления появится точно на i - м такте.
Этот результат можно получить, если в схеме деления убрать вход, а цепь обратной связи подать непосредственно на вход ячейки r0. При этом для генерирования элементов поля как последовательности степеней αi в виде m-значных двоичных чисел, записанных в ячейках регистра необходимо предварительно в ячейку r0 записать «1». В этом случае в исходном состоянии на нулевом такте работы рассматриваемой схемы как генератора элементов GF(2m) будет записан остаток от деления x0 на g(x). Элемент поля αi появится в регистре на i -м такте, что соответствует подаче на вход схемы деления xi на нулевом такте.
Все 2m-1 не нулевых элементов GF(2m), будут получены за 2m-1 тактов работы схемы. До m-1 такта работы схемы включительно регистр будет содержать в своих ячейках только одну единицу и m -1 нулей. На m -м такте содержимое регистра станет равным g'(x)=g(x)+xm, где g'(x)- многочлен, состоящий из всех слагаемых g(x), кроме слагаемого старшей степени xm. В силу того, что g(x) принадлежит идеалу, т.е. {g(x)}={0}, получаем g’(x)=xm.
Продолжая сдвиги, получим, что на m+1 такте содержимое ячеек регистра будет соответствовать xg(x), т.е. подаче на вход схемы деления на нулевом такте xm+1 и т.д. Так будет продолжаться до тех пор, пока содержимое ячеек регистра не станет эквивалентным подаче на вход схемы деления xn. Это состояние регистра соответствует α0=1,т.к. xn=1(см.6.1). В силу того, что многочлен g(x) примитивен, он принадлежит показателю n=2m-1. Это означает, что до возвращения в состояние α0=1 в регистре генератора на различных тактах работы появятся с учётом нулевого такта все ненулевые последовательности длины m и каждая только один раз.
Проиллюстрируем изложенное примером 6.15
Пример 6.15. Построим генератор элементов поля GF(23). Для этой цели используем примитивный многочлен 1+x+x3. Класс вычетов {x}= α является корнем 1+x+x3 и примитивным элементом поля GF(23). Схема генератора элементов поля GF(23) и пояснение ее работы представлены на рис. 6.9.


“1
| Такты | Последовательность длины 3 | Многочлен | Степень α |
| (1 0 0) (0 1 0) (0 0 1) (1 1 0) (0 1 1) (1 1 1) (1 0 1) (1 0 0) | α α 2 1 + α α + α2 1 + α + α2 1 + α2 | α 0 α 1 α 2 α 3 α 4 α 5 α6 α7 =α0 |
Рис 6.9 Генератор элементов поля GF(23)
Предварительно в ячейку α0 записывается «1». После этого осуществляются сдвиги. Выходом генератора является содержимое ячеек α0,α1,α2. Работа генератора поясняется изменением содержания и представлением двоичной последовательности многочленом и степенью примитивного элемента α1
Дата добавления: 2015-08-02; просмотров: 136 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Схема для умножения на многочлен | | | Схемы кодирующих устройств циклических кодов |