Определение и основные свойства

Коды Рида-Соломона – или РС-коды – относятся к недвоичным циклическим кодам, т.е. кодам, символы которых взяты из конечного поля, содержащего q >2 элементов и обозначаемого GF (q), где q – степень некоторого простого числа. Понятие о конечных полях кратко изложено в 6.1.

Пусть необходимо передать по каналу связи последовательность из M двоичных элементов вида:

111 … 1 101 … 1 011 … 0 100 … 1.

Разобьем эту последовательность на блоки по m элементов и обозначим их через некоторые символы β₀, β₁, β₂, …, β_N–1, где . Полное число различных значений m -элементных блоков равно q =2 ^m.

Таким образом, передаваемая последовательность представляется в виде некоторой q -ичной последовательности: β₀, β ₁, …, β _S, …, β _N–1.

Некоторая совокупность q -ичных последовательностей образует q -ичный код. Такие коды, как и двоичные коды, могут быть простыми и помехоустойчивыми.

Кодовые комбинации q -ичного кода могут быть представлены в виде многочленов с q -ичными коэффициентами – элементами поля GF (q). При этом q -ичные коэффициенты как элементы поля GF (q) являются в рассмотренном примере многочленами с двоичными коэффициентами.

Например:

B(x)=β ₀ (z)x⁰+ β ₁ (z)x¹ + … + β _N–1x^N–1,

где: β _i(z)=b₀z⁰+ b₁z¹ + … + b_m–1z^m–1.

Здесь b_i =0,1, а z – формальная переменная многочлена с двоичными коэффициентами.

Кодом Рида-Соломона (РС-кодом) называют циклический (N,K)-код, при N=q–1, множество кодовых комбинаций которого представляется многочленами степени N–1 и менее с коэффициентами из поля GF(q), где q>2 и является степенью простого числа, а корнями порождающего многочлена являются N–K последовательных степеней: α, α ², α ³, …, α ^D–1, некоторого элемента αÎGF(q), где D– минимальное кодовое расстояние (N,K)-кода.

Из определения вытекает, что РС-код является подклассом БЧХ-кодов с m ₀=1 [1]. Обычно считают элемент α¹ примитивным элементом поля GF (q), т.е. все степени α от 0-й до (q –1)-й являются всеми различными ненулевыми элементами поля GF (q). Порождающий многочлен РС-кода имеет степень N – K = D –1 и по теореме Безу может быть найден в виде произведения

.

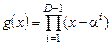В соответствии с теорией циклических кодов, порождающий многочлен g (x) является делителем x^N –1 над GF(q).

Таким образом, РС-код над полем GF(q) имеет длину кодовой комбинации N=q–1, число избыточных элементов в ней N – K = D –1 и минимальное кодовое расстояние D=N–K+1(граница Синглтона).

Коды с подобным значением минимального кодового расстояния в теории кодирования получили название максимальных, или кодами с максимально достижимым расстоянием.

При фиксированных N и K не существует кода, у которого минимальное кодовое расстояние больше, чем у РС-кода. Этот факт часто является веским основанием для использования РС-кодов. В то же время РС-коды всегда оказываются короче всех других циклических кодов над тем же алфавитом. РС-коды длины N < q –1 называют укороченными, а коды длины q (или q +1) – расширенными (удлиненными) на один (или два) символа. В РС-коде может быть выбрано и другое значение m ₀, если это оправдано.

Рассмотрим некоторые примеры на построение РС-кодов.

Дата добавления: 2015-08-02