
Читайте также:
|
У. Питерсон [1] представил ключевое уравнение в матричной форме:

Таким образом, задача определения коэффициентов многочлена локаторов ошибок сводится к прямому решению системы v линейных уравнений с v неизвестными.
б) Алгоритм Евклида.
Известно, что, если существует наибольший общий делитель d(x)двух многочленов а(х) и b(х), тосуществуют многочлены f(x) и g(x) такие, что справедливо: a(x)f{x)+b(x)g(x)=d(x).
Многочлен d(x) может быть найден по алгоритму Евклида, который состоит в последовательном делении с остатком а(х) на b(х), затем b(х) на первый остаток r1(х),затем r1(х) на второй остаток r2(х) ит.д.
При декодировании кодов БЧХ интересуются не конечным результатом алгоритма Евклида, а промежуточными результатами, которые можно представить в виде: a(x)f(x)+b(x)g(x)=r(x).
У. Сугияма и его соавторы [3] использовали этот результат для решения ключевого уравнения следующим образом: b(x)g(x)= ri(x) (mod a(x)),полагая,
а(х)=х2t, b(x)=S(x), gl(x)=Λi(x), ri(x)=Ωi(x).
При этом используется свойство алгоритма Евклида:
deg[gi(x)]+deg[ri-l(x)]=deg[a(x)].
Если а(х)=х2t, то deg[Λi(x)]+deg[Ωi-l(x))=2t,
deg[Λi(x)]+deg[Ωi(x))<2t.
При появлении v≤t ошибок имеем: deg[Ω(x)]< deg[Λ (x)] ≤t.
Существует единственный с точностью до постоянного множителя (элемента поля) многочлен Λ(х) степени ≤ t, удовлетворяющий уравнению:
Ωi(x) =S(x) Λi(x) (mod x2t),
если deg[Ωi-1(x)]≥ t при deg[Λi(x)]≤ t
и deg[Ωi(x)]< t при deg[Λi+1,(x)] > t.
Поэтому промежуточные результаты на I-ом шаге дают единственное интересующее нас решение ключевого уравнения.
Таким образом, для решения ключевого уравнения следует применять алгоритм Евклида до тех пор, пока не будет выполнено условие
deg[Ωi(x)]< t.
Итак, алгоритм Евклида решения ключевого уравнения по методу У. Сугиямы и др. сводится к следующему:
1. Применить алгоритм Евклида к а(х)=х2t и b(x)=S(x).
2. Использовать начальные условия:
Λ-1(х)=0,
Λ0(х)=1,
Ω-1(x)=x2t,
Ω0(x)=S(x).
3. Остановиться, если deg[Ωi(x)]< t.
4. Положить Λ(х)= Λi(x) и Ω(x)= Ωi(x).
При вычислении значений Λi(x) и Ωi(x) следует использовать свойство алгоритма Евклида: каждое из значений Λi(x) и Ωi(x) получается из двух предшествующих значений по следующей общей формуле:
Ei(x)=Ei-2(x)+qi(х)Ei-1(x), где 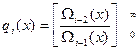 .
.
В квадратных скобках записано частное от деления указанных многочленов т,е. многочлен степени 0 и более.
в) Алгоритм Берлекемпа-Месси.
На рис.7.1 представ л ен доработанный алгоритм, позволяющий кроме А(х) получать также и многочлен значений ошибок и Ω(x).
Этот алгоритм был предложен Э. Берлекемпом и Дж. Месси[4] как итеративный процесс построения минимального линейного регистра сдвига с обратной связью, аналогичного схеме решения разностных уравнений, генерирующего все компоненты синдромного многочлена S(x) no υ первым.
Целью алгоритма является нахождение коэффициентов многочлена локаторов ошибок Λ(х), значение которых определяет вид обратных связей регистра.
Дата добавления: 2015-08-02; просмотров: 126 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Многочлен значений ошибок | | | Примеры решения ключевого уравнения |