Примеры решения ключевого уравнения

Рассмотрим примеры применения рассмотренных алгоритмов для декодирования с исправлением ошибок кодами Рида-Соломона.

Пример 7.7. Пусть над полем GF(2³) с элементами 000, α=1=100, α¹=010, α²=001,

α³=110_, α⁴=011, α⁵=111, α⁶=101 построен код Рида-Соломона (7,3) с d_min=5, способный исправлять 2-х кратные ошибки. Корнями порождающего многочлена являются следующие элементы GF(2³): α¹=010, α²=110,α³=110,α⁴=011.. Порождающий многочлен кода имеет вид;

g(x)=(x+α)(x+α²)(x+α³)(x+α⁴)=α³+α¹x+α⁰x²+α³x³+x⁴

Предположим, что по каналу связи была передана комбинация (0000000),а на вход декодера поступила комбинация. f(x)=а²х³ + а⁵х⁴. Схема вычисления синдрома определила компоненты синдромного многочлена:

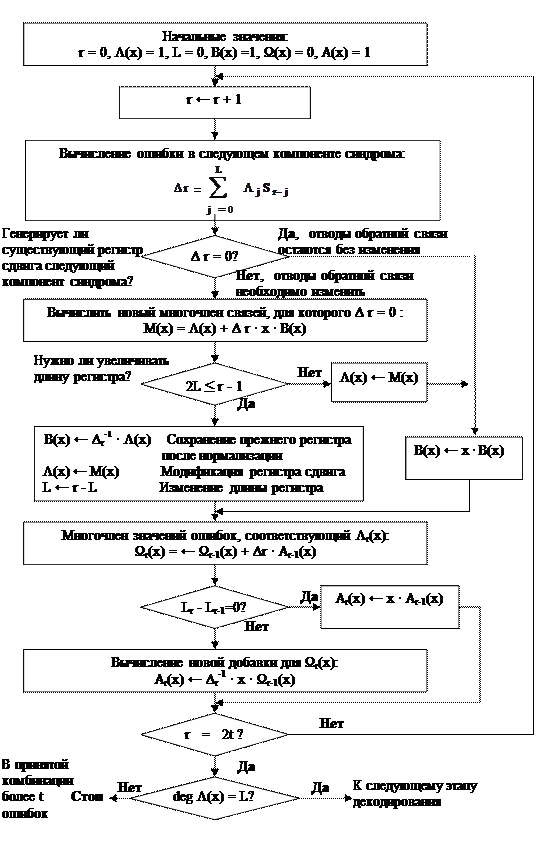
Рис.7.1.Алгоритм Берлекемпа-Месси

S₁=f(x=α)=α⁵+α²=α³

S₂=f(x=α²)=α¹+α⁶=α⁵

S₃=f(x=α³)=α⁴+α³=α⁶

S₄=f(x=α⁴)=α⁰+α⁰=0

При вычислении значений элементов S_i, показатели степеней элементов поля приводятся по mod 7, т.к. для GF(2³) а⁰=а⁷=1. Итак, для принятой комбинации синдромный многочлен имеет вид: S(x)=α³+α⁵x+α⁶x².

Определим для принятой комбинации многочлен локаторов ошибок Λ(х).

1.Алгоритм Питерсона. Матричное уравнение для нахождения компонентов Λ(х) по S(х) имеет вид:

.

В предложении, что произошло максимальное число исправляемых кодом ошибок t=2 воспользуемся теоремой Крамера [5] для решения системы линейных уравнений, представленных в матричной форме Ах=С, в случае, когда det А существует и отличен от нуля, В этом случае система имеет одно определенное решение, и каждое из неизвестных выражается частным двух определителей, причем в знаменателе стоит определитель |А|, а в числителе, определитель который из него получается заменой коэффициентов при определяемом неизвестном соответствующими свободными членами: .

Применяя теорему Крамера для нахождения λ i получаем:

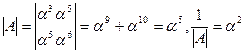
Таким образом, многочлен локаторов ошибок имеет вид:

Λ(x)=1+α⁶x+α⁰x².

Корнями многочлена Λ{х) являются элементы GF(2³): α³ и α⁴, т.е. локаторы ошибок

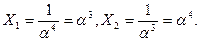
Это дает возможность представить многочлен локаторов ошибок и виде;

Λ(х)=(1+α³х)(1+α⁴х)\

Алгоритм Питерсона позволяет найти также и значения ошибок. Для этого выразим компоненты синдромного многочлена S₁ и S₂ через локаторы ошибок X_l, и значения ошибок Y_l:

S₁=Y₁X₁ + Y₂X₂

S₂=Y₁X₁² + Y₂X₂

Представим эти уравнения в матричной форме:

или

Решим это уравнение тем же способом, каким были найдены λ₁ λ₂ .Вычислим определитель:

.

Теперь находим:

=α(α⁴+α²)=α⁵+α³=α² , =α(α+α²)=α²+α³=α⁵.

Полученные значения Y₁ и Y₂ соответствуют коэффициентам многочлена ошибок.

2.Алгоритм Евклида

Поиск значений Λ_i(x) в Ω_i(x), удовлетворяющих приведенным выше критериям, представим в виде таблицы.

i	-1
Λi(x)			α+х+αx^2=α(1+α^6x+x^2)
Ωi(x)	х^4	S(x)	α^4+α^4х=α(α^3+α^3х)
qi(x)	___	___	[х^4/S(x)]=α+x+αx^2

Из приведенной таблицы видно, что найденное значение Λ (х)=α(1+ α⁶x+x²) отличается от Λ (х), подученного по алгоритму Питерсона, постоянным сомножителем α. Понятно, что корни этих многочленов совпадают, т,е, постоянный сомножитель не влияет на определение локаторов ошибок.

3, Алгоритм Берлекемпа-Месси. Вычисление Λ(х) и Ω(x) в соответствии с доработанным алгоритмом Берлекемпа-Месси представим ввиде следующей таблицы:

r	S r	Δr	M(x)	B(x)	Λ(x)	L	Ω(x)	A(x)
	α^3	α^3	1+α^3x	α^4	1+α^3x		α^3
	α^5	α	1+α^2x	a^4x	1+α^2x		α^3
	α^6	α^2	1+α^2x+α^6x	α^5+x	1+α^2x+a^6x^2		α^3	αx

α^2

1+α^6x+x^2

α^5x+x^2

1+α^6x+x^2

α^3+ α^3x

αx

Найденному значению Λ(х)= 1+α⁶x+x² соответствует регистр сдвига с обратными связями, определенными видом Λ(х), длины L=2, способный генерировать все компоненты синдромного многочлена по двум младшим. Этот регистр имеет вид:

В исходном состоянии в ячейках памяти регистра записаны компоненты синдрома S₁₌α³ и S₂=α⁵. По первому такту S₁₌α³ поступает на выход, а в ячейках остаются S₂=α⁵ и S₃=α⁶. По второму такту S₂=α⁵ поступает на выход, а в ячейках остаются S₃=α⁶ и S₄=0, которые за два следующих такта поступают на выход.

4. Алгоритм Форни.

Для вычисления значений ошибок необходимо знание Λ(х) и его корней, а также должен быть известен многочлен Ω(x).Непосредственным вычислением находим: ■

Ω(x)=S(x)Λ(x)(modx^2t)=(α³+α⁵x+а⁶х²)(1+α⁶x+x²)(modx⁴)=α³+α³х. Расчетные значения Λ(х) и Ω(x)полностью совпадают с полученными по алгоритму Берлекемпа-Месси и отличаются постоянным сомножителем при вычислении по алгоритму Евклида.

Для нахождения значений ошибок по алгоритму Форни найдем Λ^′ (х)=а⁶. Подставляя в Ω(х) вместо x значения корней Λ(x) получаем:

Итак, вычисленное значение многочлена ошибок е(х)= α²x³+α⁵x⁴ полностью совпадает с принятой комбинацией f(х) и, следовательно, по каналу связи передавалась комбинация (0000000).

Дата добавления: 2015-08-02